Теорема об умножении вероятности

Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий. Например, событие А – деталь годная, событие В – деталь окрашена. Тогда произведение АВ – деталь годна и окрашена.

Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий.

Условной вероятностью Р_А(В) будем называть вероятность события В, вычисленную в предположении, что событие А уже наступило:

Р_А(В) = Р(АВ)/Р(А), где Р(А)>0.

Теорема умножения вероятностей: вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

Р(АВ) = Р(А)Р_А(В)

Следствия: 1. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:

2. Пусть событие В независимо от события А, если появление события А не изменяет вероятности события В. При этом условная вероятность события В равна его безусловной вероятности (т. е. вероятности события, вычисленной без ограничений): Р_А(В) = Р(В). Тогда вероятность совместного появления нескольких независимых событий равна произведению вероятностей этих событий:

Р(А₁А₂…А_n) = Р(А₁)Р(А₂)…Р(А_n)

Теорема о сложении вероятности совместных и несовместных событий

Суммой событий A и B называют событие, состоящее в появлении события А, или события В, или обоих этих событий. Например, событие А соответствует работоспособности первого прибора, событие В - работоспособности второго прибора. Тогда сумма А+В соответствует тому, что работоспособен будет как минимум один прибор.

В частности, если два события А и В - несовместные, то А+В - это событие, состоящее в появлении одного из этих событий, безразлично какого.

Теорема сложения вероятностей несовместных событий: вероятность появления одного из группы несовместных событий, безразлично какого, равна сумме вероятностей наступления каждого из этих событий.

P(A+B+…+Z) = P(A) + P(B) + … + P(Z)

Следствия: 1. Сумма вероятностей событий А₁, А₂, … , А_n, образующих полную группу, равна единице:

P(A₁) + P(A₂) + … + P(A_n)=1

2. Сумма вероятностей противоположных событий равна единице.

Теорема сложения вероятностей совместных событий: вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления: P(A+B) = P(A) + P(B) – P(AB)

Формула полной вероятности. Формула гипотез

Пусть событие А может наступить только при условии появления одного из несовместных событий В₁, В₂, …, В_n, которые образуют полную группу, а вероятности этих событий P_В1(A), P_В2(А), … , P_Вn(A). Найти вероятность события А помогает формула полной вероятности.

Теорема. Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий В₁, В₂, … , В_n, образующих полную группу, равна сумме произведений вероятностей каждого их этих событий на соответствующую условную вероятность события А:

P(A) = P(B₁) P_B1(A)+P(B₂) P_В2(A)+…+P(B_n) P_Bn(A)

Теорема гипотез

Пусть событие А может наступить при условии появления одного из несовместных событий B₁, B₂, …, B_n, образующих полную группу. Поскольку не известно, какое из них наступит, их называют гипотезами. Вероятность появления события А определяется по формуле полной вероятности:

P(A) = P(B₁) P_B1(A)+P(B₂) P_B2(A)+…+P(B_n) P_Bn(A)

Допустим, что произведено испытание событие А произошло. То, что оно произошло, изменит вероятности гипотез Р(В₁), …, Р(В_n). Требуется определить условные вероятности осуществления этих гипотез в предположении, что событие А произошло, т.е. определить: P_А(B₁), P_А(B₂), …, P_А(B_n).

Решение:

Найдем вероятность P(АB₁) = P(B₁) P_В1(A) = P(A) P_А(B₁),

Отсюда: .

Заменив здесь P(A) по формуле полной вероятности, получим:

,

Таким же образом определяются условные вероятности остальных гипотез В итоге получаем:

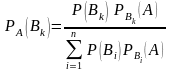
Данная формула называется формулой Байеса или теоремой (формулой) гипотез.