1. События и их виды

2. Вероятность и ее свойства

3. Теория о сложении, умножении вероятности

4. Формула гипотез

5. Дискретные непрерывные случайные величины. Их законы распределения и численные характеристики.

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Ивановский государственный энергетический

университет имени В.И.Ленина»

кафедра АТП

Реферат по надежности

Выполнила:

студентка гр. III-8*

Александрова О. В.

Проверил:

преподаватель

Тетеревков И.В.

Иваново 2010

Содержание

1. События и их виды

2. Вероятность и ее свойства

3. Теорема об умножении вероятности

4. Теорема о сложении вероятности совместных и несовместных событий

5. Формула полной вероятности, формула гипотез

6. Случайные величины. Закон распределения непрерывной и дискретной случайной величины

7. Моменты распределения, характеристики закона распределения

8. Литература

События и их виды

Событие – это некий факт, который в результате проведения испытания (иначе говоря, в результате опыта) может произойти или не произойти.

По своим свойствам все события делятся на три вида:

• достоверные;

• невозможные;

• случайные.

Достоверным называют событие, которое обязательно произойдет, если будет выполнено определенное условие или группа условий.

Невозможным называют событие, которое заведомо не произойдет, если выполнится некоторая совокупность условий.

Случайным называют событие, которое при выполнении определенных условий может либо произойти, либо не произойти.

Набор из двух и более событий называют группой событий. Если в результате опыта обязательно произойдет одно из событий группы, то группа называется полной.

По тому, как несколько событий соотносятся друг с другом, события разделяют на:

• совместные;

• несовместные.

Несовместными называют события, если появление одного из них полностью исключает появление других событий в одно и том же испытании.

Совместными называют события, если наступление одного события не препятствует наступлению других.

Противоположными называются два единственно возможных события, составляющие полную группу.

События называют равновозможными или равновероятными, если есть основания считать, что ни одно из них не является более возможным, чем другое.

Вероятность и ее свойства

Вероятность – это число, характеризующее степень возможности появления некоторого события.

Каждый из равновозможных результатов испытания называется элементарным исходом. Элементарный исход, соответствующий наступлению желаемого события, называется благоприятствующим.

Вероятностью события А называют отношение числа исходов m, благоприятствующих появлению этого события, к общему числу всех равновозможных несовместных элементарных исходов n, образующих полную группу:

P(A) = m/n.

На практике число элементарных исходов может быть бесконечным, причем трудно утверждать, что эти исходы равновероятны. Поэтому в качестве оценки вероятности используют относительную частоту. Относительная частота появления события равна отношению числа испытаний m, в которых это событие наступило, к общему числу проведенных испытаний n:

W(A) = m/n.

Классическое определение вероятности не требует физического проведения испытаний, определение относительной частоты предполагает, что испытания были реально произведены. При большом количестве испытаний (если они проводились в равных условиях) относительная частота изменяется мало, приближаясь к вероятности наступления события.

Основные свойства вероятности: 1. Вероятность достоверного события равна единице. Если событие достоверно, то любой элементарный исход испытания благоприятствует появлению этого события.

В этом случае m = n, следовательно,

P(A) = m/n = n/n = 1.

2. Вероятность невозможного события равна нулю. Если наступление события невозможно, то ни один из элементарных исходов испытания не благоприятствует его появлению.

В этом случае m = 0, следовательно,

P(A) = m/n = 0/n = 0.

3. Вероятность случайного события есть положительное число из диапазона от нуля до единицы. Действительно, случайному событию благоприятствует лишь часть из общего числа элементарных исходов испытания.

В этом случае 0< m< n, значит, 0<m/n<1, следовательно,

0 < P(A) < 1.

Вывод: вероятность любого события удовлетворяет двойному неравенству:

0 ≤ Р(А) ≤ 1.

Теорема об умножении вероятности

Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий.

Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий.

Геометрическая интерпретация понятия произведение событий:

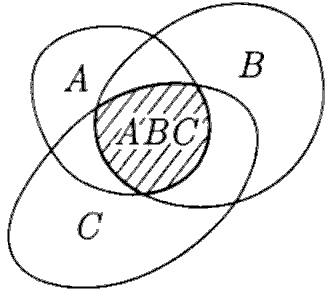
Рис.1

Если события А, В и С есть попадание точки соответственно в области А, В и С, то событие АВС есть попадание в область, заштрихованную на рис.1.

Условной вероятностью Р_А(В) будем называть вероятность события В, вычисленную в предположении, что событие А уже наступило:

Р_А(В) = Р(АВ)/Р(А), где Р(А)>0.

Теорема умножения вероятностей: вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

Р(АВ) = Р(А)Р_А(В)

Следствия: 1. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении, что все предыдущие события уже появились:

Р(А₁А₂…А_n)=Р(А₁)·Р_А1(А₂)·Р_А1А2(А₃)·…·Р_{А1А2…Аn-1}(А_n).

2. Пусть событие В независимо от события А, если наступление события А не изменяет вероятности появления события В. При этом условная вероятность события В равна его безусловной вероятности (т. е. вероятности события, вычисленной без ограничений): Р_А(В) = Р(В). Тогда вероятность совместного появления нескольких независимых событий равна произведению вероятностей этих событий:

Р(А₁А₂…А_n) = Р(А₁)Р(А₂)…Р(А_n).

Теорема о сложении вероятности совместных и несовместных событий

Суммой событий A и B называют событие, состоящее в появлении события А или события В, или обоих этих событий.

В частности, если два события А и В - несовместные, то А+В - это событие, состоящее в появлении одного из этих событий, безразлично какого.

Геометрическая интерпретация понятия сумма событий:

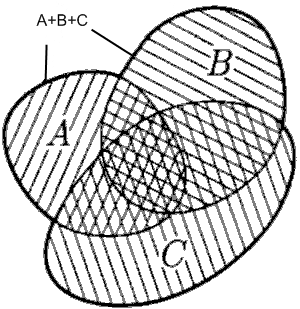
Рис.2

Если события А, В и С есть попадание точки соответственно в области А, В и С, то событие А+В+С есть попадание в область, заштрихованную на рис.2.

Теорема сложения вероятностей несовместных событий: вероятность появления одного из группы несовместных событий, безразлично какого, равна сумме вероятностей наступления каждого из этих событий:

P(A+B+…+Z) = P(A) + P(B) + … + P(Z).

Следствия: 1. Сумма вероятностей наступления событий А₁, А₂, … , А_n, образующих полную группу, равна единице:

P(A₁) + P(A₂) + … + P(A_n)=1.

2. Сумма вероятностей наступления событий А и Ā, противоположных друг другу, равна единице:

Р(А)+Р(Ā)=1.

Теорема сложения вероятностей совместных событий: вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления:

P(A+B) = P(A) + P(B) – P(AB).

Приведенные теоремы широко применяются в теории надежности.

Формула полной вероятности, формула гипотез.

Следствием обеих основных теорем - теоремы о сложении вероят­ностей и теоремы об умножении вероятностей - является так называ­емая формула полной вероятности.

Пусть событие А может наступить только при условии появления одного из несовместных событий В₁, В₂, …, В_n, которые образуют полную группу, будем эти события называть гипотезами. Вероятности этих событий соответственно равны P_В1(A), P_В2(А), … , P_Вn(A).

Докажем, что в этом случае

P(A) = P(B₁) P_B1(A)+P(B₂) P_В2(A)+…+P(B_n) P_Bn(A)

т.е. вероятность события А вычисляется как сумма произведений вероятности каждой гипотезы на вероятность события при этой гипотезе.

Эта формула носит название формулы полной вероятности.

Доказательство:

Так как гипотезы В₁,В₂, ..., В_n образуют полную группу, то событие А может появиться только в комбинации с какой-либо из этих гипотез:

А = В₁А + В₂А + ... + В_пА.

Так как гипотезы В₁, В₂, ..., В_п несовместны, то и комбинации В₁ А, В₂А, ..., В_nА также несовместны, применяя к ним теорему сложения, получим

Р(А) = Р(В₁А) +Р(В₂А)+...+ Р(В_пА) =

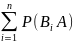
Применяя к событию В_iA теорему умножения, получим

что и требовалось доказать.

Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий В₁, В₂, … , В_n, гипотез, образующих полную группу, равна сумме произведений вероятностей каждого их этих событий на соответствующую условную вероятность события А.

Следствием теоремы умножения и формулы полной вероятности является так называемая теорема (формула) гипотез, или формула Бейеса.

Пусть событие А может наступить при условии появления одного из несовместных событий B₁, B₂, …, B_n, образующих полную группу. Поскольку неизвестно, какое из них наступит, их называют гипотезами. Вероятность появления события А определяется по формуле полной вероятности:

P(A) = P(B₁) P_B1(A)+P(B₂) P_B2(A)+…+P(B_n) P_Bn(A)

Допустим, что произведено испытание, событие А произошло. То, что оно произошло, изменит вероятности гипотез Р(В₁), …, Р(В_n). Требуется определить условные вероятности осуществления этих гипотез в предположении, что событие А произошло, т.е. определить: P_А(B₁), P_А(B₂), …, P_А(B_n).

Решение:

Найдем вероятность P(АB₁) = P(B₁) P_В1(A) = P(A) P_А(B₁),

Отсюда: .

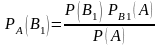Заменив здесь P(A) по формуле полной вероятности, получим:

,

Таким же образом определяются условные вероятности остальных гипотез. В итоге получаем:

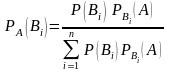i=1,2,…,n

Полученную формулу называют формулой Бейеса. Она позволяет переоценить вероятности гипотез после того, как становится известным результат испытаний, в итоге которого появилось событие А.

Случайные величины. Закон распределения непрерывной и дискретной случайной величины.

Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.

Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным и бесконечным.

Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного или бесконечного промежутка. Очевидно, число возможных значений непрерывной случайной величины бесконечно.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически и графически.

Существует несколько видов распределения. Вот некоторые из них.