Практичне заняття № 1,2

Питання для самоконтролю до розділу 1

1. У чому сутність фінансово-кредитних розрахунків?

2. Чому навчає фінансова математика?

3. Поясніть необхідність опанування інструментарієм фінансових розрахунків. Відповідь побудуйте за схемою:

Я вважаю, що опанування методами фінансових розрахунків потрібно для … . Тому, що… . Наприклад, … . Таким чином, … .

4. Наведіть приклади ситуацій, в яких виникає необхідність застосування апарату фінансової математики.

5. Що, на Вашу думку, повинно бути наступним кроком після отримання кількісного результату фінансової задачі?

6. Як Ви розумієте принцип нерівноцінності грошей у часі?

7. Як Ви розумієте поняття відсоткової ставки?

8. В чому сутність відсотка? Наведіть приклади, в яких виникає необхідність розуміння сутності відсотка.

9. Як Ви розумієте поняття відсотків у фінансових розрахунках?

10. Спробуйте описати будь-яку конкретну фінансово-кредитну угоду, використовуючи поняття відсоткової ставки.

Задача 1. Число збільшилось у 2,7 разів. На скільки відсотків збільшилось число?

Розв’язання. Нехай початкове число дорівнює х, тоді збільшене число – 2,7· х. Якщо прийняти число х за 100 %, тоді число 2,7·х складає 270 %, що, у свою чергу, на 170 % більше початкової величини.

Задача 2. У скільки разів збільшилася первинна грошова сума, якщо відомо, що вона підвищилася на 200 %?

Розв’язання. Сума збільшується у 3 рази, тому що до початкової суми, яку приймаємо за 100 %, додається 200 %. В результаті маємо 300 %, що по відношенню до початкової величини є втричі більшим.

Задача 3. Спочатку ціна товару збільшилася на 40%,а потім - зменшилася на 20%. Що відбулося з первинною ціною товару?

Розв’язання. Нехай початкова ціна буде дорівнювати х, тоді при збільшенні її на 40 % вона буде становити 1,4·х.

Зменшення ціни на 20 % приводить до значення: 1,4·х – 0,2·1,4·х =1,12·х. Отже, початкова ціна збільшилася на 12 % або в 1,12 рази.

Задача 4. Число а на 20 % менше числа b. Яку частину складає число а від числа b?

Розв’язання. За умовою число а становить 80% від числа b, звідки a = 0,8·b. Отже, число а складає 8/10 або 4/5 від числа b.

Задача 5. При продажу товару за 1386 грн. одержано 10 % прибутку. Знайти собівартість товару.

Розв’язання. Якщо визначити ціну 1386 грн. як 110 % (враховуючи прибуток), то собівартість товару, тобто 100 %, становитиме

1260 (грн.).

Задача 6. Господарство, продавши продукції на 3348 грн., понесло 4 % збитку. Яка собівартість продукції?

Розв’язання. Якщо визначити ціну 3348 грн. як 96 % (враховуючи збиток), то собівартість товару визначається із співвідношення:

3487,5 (грн.)

Задача 7. На яку суму господарство має продати продукцію, щоб одержати 4 % прибутку, якщо собівартість продукції становить 3348 грн.?

Розв’язання. Якщо визначити ціну 3348 грн. як 100 %, то доход господарства визначається із співвідношення:

3481,92 (грн.).

Задача 8. Який прибуток отримало господарство, якщо воно продало продукцію на 3484 грн., а собівартість продукції становить 3350 грн.?

Розв’язання. Якщо визначити собівартість 3350 грн. як 100 %, то прибуток господарства становить 3484 – 3350 = 134 (грн.), що у відсотковому вираженні дорівнює:

4 %.

Задачі, рекомендовані до розв’язання на практичних заняттях за розділом 1

1. Число збільшилося на 23 %. У скільки разів збільшилося це число?

2. Число збільшилося в 3,7 рази. На скільки відсотків збільшилося це число?

3. Число d на 23% менше числа с. Яку частину складає число d від числа с?

4. Податок на додану вартість (ПДВ) дорівнює 18% ціни товару. Знайти ПДВ, якщо товар з урахуванням ПДВ коштує 2959 грн.

5. Спочатку ціна товару збільшилася на 30 %, а потім нова ціна зменшилася на 15 %. Що відбулося з первинною ціною товару?

6. Спочатку ціна товару збільшилася на 50 %, а потім повернулася до первинного рівня. На скільки відсотків зменшилася нова ціна товару?

7. У результаті інфляції ціни зросли на 300 %. Визначте, на скільки відсотків потрібно знизити ціни, щоб повернути їх до попереднього рівня.

8. Визначте, яку суму потрібно покласти на рахунок, щоб через рік отримати 800 грн. прибутку, якщо банк сплачує своїм вкладникам 20 % річних?

9. У бізнесмена дохід за попередній рік склав 200 тис. грн. У цьому році він намагається отримати 600 тис. грн. На скільки відсотків повинен зрости дохід?

10. Товар подешевшав на 30 %. На скільки відсотків більше можна купити товару на ту саму суму коштів?

Розділ 3. Прості відсотки

Приклад 1. Визначити відсотки та суму нарощення боргу, якщо позика становить 128 тис. грн., її термін складає 3 роки, відсотки – прості за ставкою 15 % річних.

Розв’язання. Використовуючи формулу (2.1), маємо:

відсотки I = 128·5·0,15=57,6 (тис. грн.),

нарощена сума S = 128+57,6=185,6 (тис. грн.).

Коефіцієнт нарощення дорівнює , тобто сума боргу зросла в 1,45 разів.

Приклад 2. Позика у розмірі 50 000 грн. видана з 2.02 по 1.10 (високосний рік) під 16,5 % простих річних. Яку суму повинен виплатити боржник за різними способами розрахунку простих відсотків.

Розв’язання.

1) За умови точних відсотків - 365/365:

=55 469,86 (грн.)

2) За умови комерційних відсотків - 365/360:

=55 545,83 (грн.)

3) За умови звичайних відсотків - 360/360.

Наближену кількість днів зручно обчислювати, виходячи з різниці кінцевої та початкової дат:

1.10	08·30-1=239 (днів).
-2.02
-1.08

Тоді =55477,08 (грн.).

Приклад 3. В угоді, розрахованої на 4 роки, прийнята ставка простих відсотків 12 % річних, а за кожен наступний рік – на 1 % більше, ніж у попередній. У скільки разів збільшиться початкова сума?

Розв’язання. Визначимо множник нарощення:

=1,54.

Отже, сума збільшиться у 1,54 рази.

Приклад 4. Через 200 днів підприємству треба буде здійснити платіж у сумі 200 тис.грн. Яку суму сьогодні необхідно розмістити на банківський депозитний рахунок з процентною ставкою 15 % річних, щоб накопичити суму, необхідну для платежу?

Розв’язання.

В задачі необхідно знайти дисконтовану суму за формулою (2.4):

179 661 (грн..)

Отже, сума, яку необхідно сьогодні розмістити на банківському депозитному рахунку, дорівнює 179 661 грн.

Приклад 5. Вексель, що має номінальну вартість 10 тис. грн., враховано в банку за ставкою дисконту 18,5 % річних за 130 днів до його погашення. Визначити суму, яку отримає власник векселя та суму, яку отримає банк.

Розв’язання. Сума, яку отримує власник векселя:

=10 000-668,0556=9 331,944 (грн.).

Сума, яку отримує банк: 668,0556 грн.

Прикладм6. Кредит для купівлі побутової техніки сумою 10 тис. грн. відкрито на 2 роки під річну відсоткову ставку 20 %. Визначити кінцеву суму боргу та суму одноразового платежу, якщо погашення кредиту здійснюється щомісяця.

Розв’язання. = 583,33 (грн.).

Тому кінцева сума боргу 14 тис. грн., а одноразовий платіж – 583,33 грн.

Приклад 7. Операція обліку приносить 19 % доходу на рік. Термін позики 98 днів. Знайти еквівалентну облікову ставку.

Розв’язання. 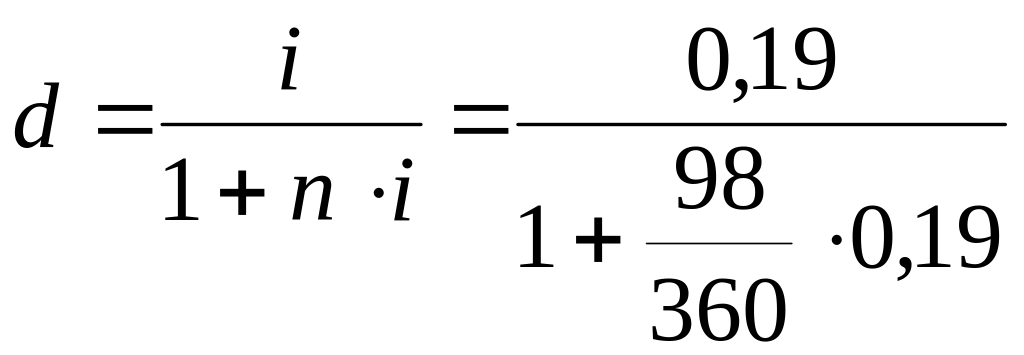=0,181, тобто d =18,1 %.

Різновидом еквівалентних ставок є середні відсоткові ставки, які є еквівалентними серії ставок.

Знаходження середньої відсоткової ставки здійснюється, коли нарахування на певну грошову суму проводиться з використанням різних ставок у різні періоди часу (або якщо нарахування проводиться на однакові суми). Отже, з формули нарощення за простою ставкою маємо:

,

звідки отримуємо формулу середньої відсоткової ставки:

, (2.10)

де n_k – тривалість k-го періоду часу, протягом якого діє ставка i_k, - сумарна тривалість всіх періодів.

Якщо необхідно знайти середню ставку для ставок, що застосовуються до різних грошових сум в різні періоди часу, то використовується формула:

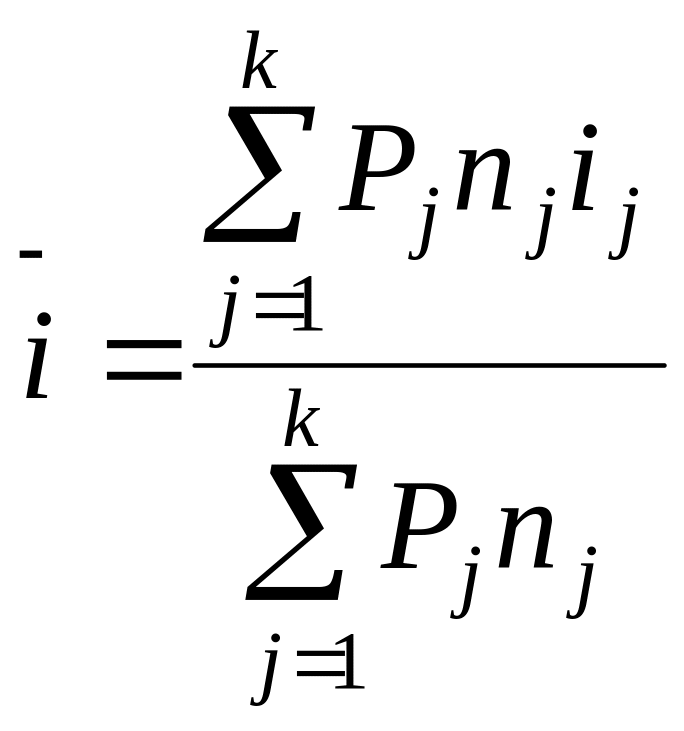. (2.11)

Приклад 8. Угода передбачає використання протягом перших 2 місяців простої ставки на рівні 20 %, наступних трьох місяців – на рівні 23%, наступних чотирьох – 25 %. Знайти середню ставку у цілому за весь період.

Розв’язання. За формулою (2.10) маємо:

=0,2322.

Отже, середня ставка простих відсотків дорівнює 23,22 %.

Приклад 9. Три платежі S₁=130 тис. грн., S₂ = 70 тис. грн., S₃=120 тис. грн. зі строками 200, 120, 170 днів відповідно, замінили одним з терміном 230 днів, нараховуючи 16 % річних простих. Обчислити суму консолідованого платежу.

Розв’язання. За формулою (2.12) маємо:

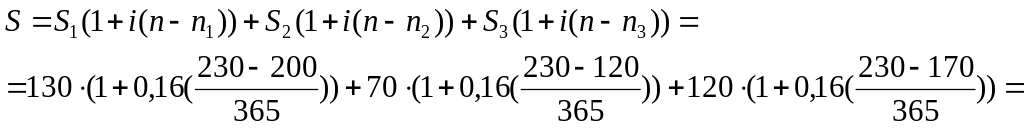
= (тис.грн.).

Приклад 10. Векселі у 20 тис.грн. з терміном 2.08 та у 15 тис. грн. з терміном 23.09 замінюються одним з продовженим терміном до 15.11, причому застосовується облікова ставка 18,5 %. Визначити суму нового векселя.

Розв’язання. Виходячи з формули (2.13), маємо:

=

= 21140,72+15419,98=36560,7 (грн.).