2.2. Средняя, среднеквадратичная и наиболее вероятная скорости молекул

Запишем теперь формулы для распределений (2.15) и (2.16) с учетом полученного значения α. Для скоростей вдоль одной из координат (пусть это будет ось х):

(2.19)

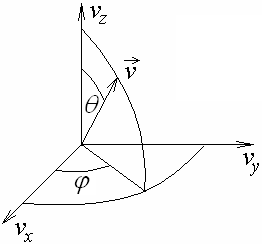
Для вектора скорости:

(2.20)

где − элемент телесного угла, в который направлен вектор скорости (см. рис. 2.1).

Рис. 2.1.

И, наконец, для абсолютной величины этого вектора:

(2.21)

Распределения (2.19)  (2.20) называются распределениями Максвелла.

Из (2.21) следует, что функция имеет максимум (см. рис.2.2, б). Этот максимум определяет наиболее вероятную скорость:

(2.22)

Рис. 2.2

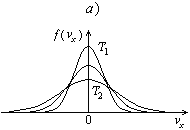
При повышении температуры доля быстрых молекул возрастает. Однако в соответствии с условием нормировки (2.14) площадь под кривой остается постоянной и равной единице. В любом случае доля очень быстрых молекул мала: и f (v_x), и (v) стремятся к нулю при стремлении величины аргумента к бесконечности.

С помощью распределения Максвелла можно найти средние значения разных величин. Для средней скорости молекул получается формула

(2.23)

Так как то среднеквадратичная скорость с учетом результата (2.17) есть

(2.24)

Как средняя, так и среднеквадратичная скорость лишь ненамного отличаются от наиболее вероятной:

Все эти скорости порядка скорости звука в газе. Для кислорода при комнатной температуре 440 м/c, для водорода она в четыре раза больше.

Средняя энергия поступательного движения молекулы

(2.5).

При комнатной температуре   3/21,3810^–1629310^–7/(1,610^–19) = 0,04 эВ, что на два порядка меньше энергии связи атома в молекуле и недостаточно для диссоциации газа.

2.3. Молекулярные пучки (потоки)

Молекулярные пучки возникают при выходе молекул газа из сосуда в вакуум через маленькое отверстие. Малые размеры отверстия позволяют считать, что молекулярный пучок не нарушает состояния равновесия в сосуде.

Выберем на поверхности сосуда некоторый элемент площади величиной S. Плотностью потока называется число частиц, падающих на этот элемент в расчете на единичную площадь в единицу времени:

(2.25)

(в сферической системе координат).

При интегрировании по углам в пределах полусферы получается плотность потока молекул с данной величиной скорости в интервале от v до v + dv:

(2.26)

Полная плотность потока для падающих со всеми скоростями частиц есть

(2.27)

где определяется соотношением (2.23).

Нормированное распределение в пучке получится, если плотность потока молекул с данной скоростью, определяемую формулой (2.25), разделить на интегральную плотность потока (2.27):

(2.28)

Здесь

(2.29)

– распределение молекул в пучке по абсолютной скорости движения, а

2.30)

– по направлениям движения. Каждое из распределений в (2.28) нормировано на единицу, т. е. и

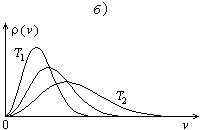
Помимо постоянного множителя, распределение (2.29) отличается от максвелловского (2.21) дополнительным множителем v. Его происхождение связано с тем, что быстрые молекулы вылетают чаще. Поэтому и средняя скорость, и средняя энергия молекул в пучке больше максвелловских средних:

(2.31)

Разница средних значений энергии молекулы в пучке и сосуде составляет kT/2 и связана исключительно с поступательным движением молекул.