5.3. Распределение по длинам пробега, средняя длина свободного пробега

_{Каждая конкретная молекула из-за молекулярного хаоса от столкновения к столкновению пробегает разный путь, который определяется набором случайных факторов. Из-за большого количества молекул правомерен вопрос о наличии непрерывной функции, характеризующей распределение молекул по длинам свободного пробега – так же, как и в рассмотренном выше случае распределения по скоростям движения. Получить эту функцию можно из довольно простых рассуждений.}

_{Пусть W(x) – вероятность того, что молекула пролетит расстояние x, не испытав столкновения. пролет без столкновения расстояния x + dx, очевидно, состоит из двух независимых событий: пролета без столкновения отрезков длиной x и dx. Вероятность столкновения на отрезке dx из-за его малости пропорциональна его длине, то есть она равна adx, где а – некий коэффициент пропорциональности (пока неизвестный). Вероятность того, что столкновения на отрезке dx не будет, есть 1 – adx. В результате имеем}

_Отсюда

_{Интегрируя полученное уравнение, находим:}

_{Константу здесь надо приравнять нулю из-за условия W(0) = 1. Тогда получим ответ в виде}

(5.5)

_{Введем вероятность dP(x) того, что столкновение произойдет на интервале от х до х + dx. Эта вероятность определяется также условием, что в интервале от 0 до х столкновений не было. Тогда получим}

_{Решение этого уравнения}

(5.6)

_{Средняя длина свободного пробега вычисляется как}

(5.7)

_{Таким образом, величина a является величиной, обратной средней длине свободного пробега, так что}

(5.8)

_{Плотностью вероятности столкновений (функцией распределения по длинам пробега) соответственно является}

(5.9)

_{Наряду с распределением по длинам пробега (5.9), можно написать с учетом соотношения x = vt распределение по временам пробега}

^(5.10)

_{где  – среднее время пробега.}

5.4. Рассеяние молекулярных пучков

_{Следует отметить, что в (5.9) x отсчитывается от произвольной точки, а не от места последнего соударения. Поэтому эта формула определяет долю частиц, пролетевших без столкновения расстояние x. Эта формула имеет значение для экспериментального определения средней длины свободного пробега молекул в газе.}

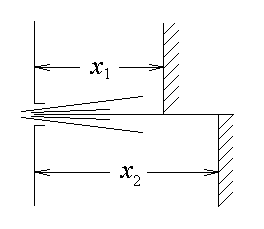
_{Опыт (рис. 5.2) состоит в следующем. Сфокусированный пучок молекул пропускается сквозь газ сравнительно низкой плотности. На пути пучка ставится охлаждаемая пластинка. Молекулы пучка, пролетевшие через газ без соударения, достигают пластинки, образуя на ней осадок. По отношению числа частиц, осевших на пластинке в двух различных положениях, находится средняя длина свободного пробега этих молекул в газе:}

Рис. 5.2

5.5. Химические превращения и химическая кинетика

_{Если имеется смесь молекул двух газов, при столкновениях между ними могут происходить химические реакции. Химические реакции описываются соответствующими уравнениями. Например, реакция между молекулами водорода и хлора приводит к образованию хлористого водорода:}

_{H2 + Cl2 = 2HCl.}

_{Однако приведенное уравнение является лишь брутто-формулой процесса. Обычно реакции протекают довольно сложным путем, который включает целый ряд промежуточных стадий.}

_{Рассмотрением механизма и скорости химических реакций занимается область химической физики, называемая химической кинетикой. Мы здесь ограничимся рассмотрением лишь некоторых существующих здесь основных понятий.}

_{Элементарными реакциями называются такие реакции, которые происходят непосредственно при взаимодействии молекул. Например, для указанного выше процесса химического взаимодействия водорода и хлора таковыми являются:}

_{H + Cl2 = HCl + Cl}

_{Cl + Н2 = HCl + Н}

_{(Есть и другие элементарные реакции, протекающие в данном процессе.) Участвующие в этой схеме атомы водорода и хлора образуются путем начального внешнего инициирования  например, воздействием светового излучения,  в дальнейшем процесс развивается цепным путем. Промежуточные частицы в химических реакциях называются интермедиатами реакций (в данном случае это атомы водорода и хлора).}

_{Элементарная реакция в газовой фазе протекает при столкновении молекул. Поэтому их скорость определяется частотой столкновения. Пусть у нас имеется два сорта молекул А и B, которые при столкновении могут вступать в реакцию и давать продукт С:}

_{А + В = С}

_{Для простоты будем считать, что массы сталкивающихся молекул существенно различаются, mB >> mA, поэтому в можно} считать, что и отсюда частота столкновений одной _{молекулы А с молекулами В есть}

_{Чтобы определить полное число столкновений в единице объема, это число надо умножить на концентрацию частиц А:}

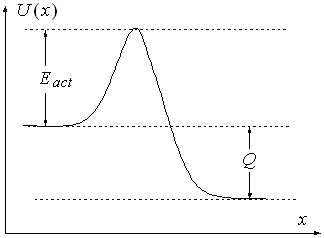
_{Теперь надо учесть, что реакция может происходить не при всяком столкновении. При сближении молекул им надо преодолеть энергетический барьер, называемый энергией активации, Eact (см. рис. 5.3).}

Рис. 5.3.

_{Вероятность преодоления барьера определяется фактором Больцмана, т. е. число молекул, преодолевающих барьер, определяется как}

_{Отметим, что при протекании реакции может выделяться или поглощаться энергия. Величина этой энергии Q (см. рис. 5.3) называется тепловым эффектом реакции.}

_{Для оценки скорости реакции еще надо ввести так называемый стерический фактор, который определяет вероятность «благоприятной» для реакции относительной ориентации частиц при соударении (для частиц из нескольких атомов не при всякой их взаимной ориентации реакция может происходить). Обозначим его за . Тогда число приводящих к реакции столкновений есть}

(5.11)

_где

– (5.12)

_{константа скорости, а}

_(5.13)

_{называется предъэкспоненциальным фактором. Его значение порядка 1010 см3/c типично для многих бимолекулярных реакций, в том числе и в жидкости.}

_{Можно написать теперь уравнение, описывающее кинетику процесса:}

(5.14)

_{Пусть начальные концентрации nA(0) = nB(0) = n0. Тогда nA(t) = nB(t) для всякого момента времени t, и решение этого уравнения выглядит как}

(5.15)

_{Отсюда можно найти концентрации веществ в любой момент времени.}

_{Как видно из (5.11), скорость превращения пропорциональна концентрациям реагирующих частиц. Этот принцип понятен из общих соображений (частоты столкновений молекул пропорциональны их концентрациям). Этот принцип остается справедливым и для реакций, в которых принимает участие большое количество разных молекул, он называется законом действующих масс.}

_{В общем случае реакции могут быть обратимыми, например}

Скорость прямой реакции здесь пропорциональна обратной  В равновесии скорости прямой и обратной реакции сравниваются. Тогда

(5.16)

_{Формально можно написать}

_{H2 + I2 – 2HI=0.}

_{В общем случае всякую реакцию можно записать аналогично:}

_{ν1A1+ ν2A2 + …= 0,}

_{где А1, А2 и т.д. – обозначения реагентов, 1, 2 и т.д. – стехиометрические коэффициенты. В указанном выше примере реакций водорода и иода 1 = 1, 2 =1, 3 = –2. Тогда в равновесии:}

(5.17)

_{Для выяснения зависимости установления равновесия от внешнего давления перейдем к относительным концентрациям ci:}

_{Тогда вместо (5.17) имеем}

(5.18)

_{Зависимость от давления отсутствует, если сумма 1 + 2 + … равна нулю. Если же в реакции полное число частиц меняется, возникает зависимость от давления. Например, для реакции синтеза аммиака}

_{N2 + 3H2 = 2 NH3}

из (5.18) имеем

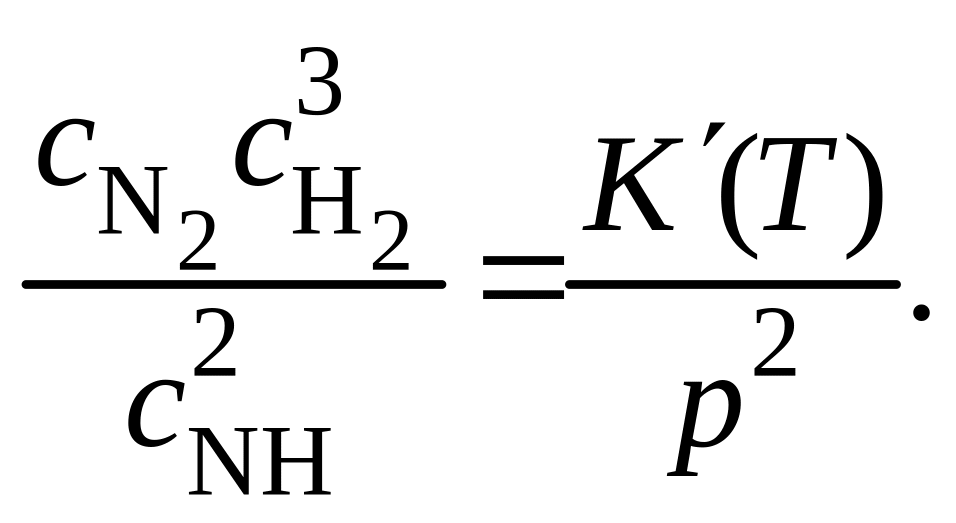(5.19)

При увеличении давления концентрации азота и водорода по сравнению с концентрацией аммиака должны уменьшаться. Это является отражением общего принципа Ле-Шателье: внешнее воздействие, выводящее систему из равновесия, стимулирует в нем процессы, стремящиеся ослабить результаты этого воздействия.