Определение и способы задания фал. Полностью и неполностью определенные фал.
При анализе и синтезе дискретных автоматов наибольшее распространение получили простые двоичные величины. Математическим аппаратом, описывающим их является алгебра логики. Логической переменной называется величина, которая может принимать одно из двух значений – 0/1. Функция алгебры логики (ФАЛ) это f(х1,х2…хN), где Х – логическая переменная. Два значения, которые принимают логические переменные и функция принято обозначать 0 и 1. Набором для ФАЛ называется какая-либо комбинация всех логических переменных, являющихся аргументами ФАЛ. Поскольку каждому набору соответствует 1 число, то полный набор – число двоичных чисел. Общее число ФАЛ n переменных определяется по формуле: N=2n. Существует несколько способов задания ФАЛ. ФАЛ считается заданной, если каждому ее набору поставлено в соответствие значение этой ФАЛ.
- Табличный способ задания. Задается таблицей истинности. При n переменных таблица содержит 2n строк и n столбцов и плюс 1 столбец, в котором находится значение функции.
Х1 |
Х2 |
Х3 |
Z |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
Графический способ. Множество значений n переменных ФАЛ поставлены в соответствие множеству вершин n-мерного единичного куба. Куб называется единичным, т. к. кажде его ребро соединяет вершины, наборы которых отличаются лишь одной переменной.
Координатный способ. Заключается в представлении ФАЛ в виде карты Карно или диаграммы Вейча.
-
Х
0
1
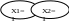
0
00
10
1
01
11
Аналитический способ. При этом функция задается в виде алгебраического выражения, в котором записываются аргументы и действия.
F(х1,х2,х3)=х1х2х3+х1х2х3+х1х2х3+х1х2х3
Числовой способ. Каждый набор считают двоичным числом, причем самую левую и самую правую часть числа считают соответственно самым старшим и самым младшим разрядом числа. Функцию задают в виде десятичных номеров тех наборов переменных для которых она принимает значение 1.
ФАЛ полностью определена, если значение функции однозначно определяется на всех наборах входных переменных. Функция неполностью (частично) определена, если существуют наборы на которых значение ФАЛ безразлично. (значок тильда ~ в соответствующей клетке таблицы состояний можно заменять любым значением, при этом значение ФАЛ, соответствующее тем наборам, где она не определена не изменится.)
Основные законы и формулы упрощения алгебры логики.
1. Сложение Х+0=Х Х+1=1 Х+Х=Х Х+Х+Х+Х+Х+Х=Х
Умножение Х*0=0 Х*1=Х Х*Х=Х Х*Х*Х*Х*Х*Х=Х
ФАЛ прямых и инверсных значений.
Х+х=1
Х*х=0
Переместительный закон.
Х1+Х2=Х2+Х1
Х1*Х2=Х2*Х1
Сочетательный закон
Х1+(Х2+Х3)=(Х1+Х2)+Х3
Х1*(Х2*Х3)=(Х1*Х2)*Х3
Распределительный закон
Х1*Х2+Х1*Х3=Х1*(Х2+Х3)
(Х1+Х2)*(Х1+Х3)=Х1*Х1+Х1*Х3+Х2*Х1+Х2*Х3=Х1*(1+Х2+Х3)+Х2*Х3=Х1+Х*Х3
Законы обращения.
х1*х2=х1+х2
х1+х2=х1*х2
Формулы поглощения
а) Х1+Х1*Х2+Х1*Х3+…+Х1*Хn=Х1*(1+Х2+Х3..)=Х1
б) Х1*(Х1+Х2)*(Х1+Х3)…(Х1+Хn)=Х1
в) Х1*(х1+Х2)=Х1*Х2
Формулы склеивания.
а) Х1*Х2+Х1*х2=Х1*(Х2+х2)=Х1
б) (Х1+Х2)*(Х1+х2)=Х1*Х1+Х1*х2+Х1*Х2+Х2*х2=Х1
в) Х1+х1*Х2=Х1+Х2