3.1.9.2 Турбулентна дифузія.

В рухомому середовищі, поряд з ламінарним рухом, має місце також і турбулентна течія середовища. При ламінарному русі має місце молекулярний перенос, при якому спостерігається тільки повздовжний перенос як кількості енергії, так і маси речовини. В турбулентному потоці виникає також і поперечний перенос, який призводить до виникнення додаткових дотичних напруг і додаткового переносу речовини. Тобто турбулентна дифузія пов'язана з турбулентністю потоку.

Перенос кількості руху

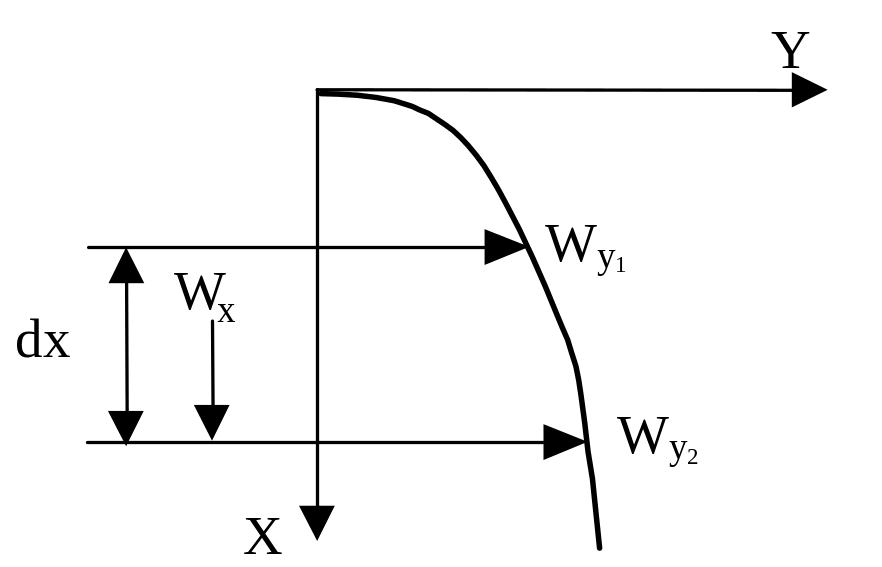
Рис. 3.9 Турбулентна дифузія

Якщо швидкість двох шарів W_y1 i W_y2, на відстані dx є неоднаковою, то різниця швидкості призводить до утворення дотичної напруги:

(3.65)

При турбулентному русі виникають вихори, які спричиняють поперечний рух зі швидкістю W_Х . Вихори зумовлюють свою дотичну напругу:

(3.66)

Тут _T – вихровий коефіцієнт турбулентної в'язкості, який залежить від від швидкості потоку, від гідродинамічної обставки і не може бути фізичною константою аналогічно µ.

3.1.9.2 Перенос енергії в турбулентному потоці

По аналогії з рівнянням молекулярного переносу тепла (рівняння Фурьє) можна записати рівняння переносу густини теплового потоку при наявності турбулентності:

(3.67)

де λ_T - коефіцієнт турбулентної теплопровідності, який залежить не від фізичних властивостей середовища, а від осереднених швидкостей турбулентного потоку, координат, напрямку руху і інших зовнішніх факторів. Інтенсивність переносу тепла за рахунок турбулентної теплопровідності λ_T визначається турбулентною температурою провідності, ,

де а_Т – аналог турбулентної дифузії _T.

Механізм турбулентного переносу кількості руху та енергії однаковий (теорія Прандтля):

3.1.9.3 Перенос маси в турбулентному потоці

По аналогії з переносом кількості руху і енергії в турбулентному потоці внаслідок турбулентних пульсацій можна записати вираз для кількості маси, що переноситься:

(3.68)

або для потоку маси, де

(3.69)

звідси,

Тут ε_Т - коефіцієнт вихрової дифузії, який не є фізичною константою, як D, а залежить від гідродинамічної обстановки потоку. Внаслідок аналогії між теплопереносом і масопереносом вважається, що, . По аналогії з коефіцієнтом молекулярної дифузії ε_Т - показує, яка кількість речовини переноситься за одиницю часу через одиницю поверхні, при одиничній різниці концентрацій на довжину 1м. ε_Т характеризує інтенсивність перемішування при масообміні.

Слід відмітити, що з розвитком турбулентності виникає повздовжне перемішування в потоці, що зменшує повздовжній градієнт концентрацій і погіршує масообмін, розділення суміші і перенос розподіленої речовини. Зменшується ефективність масопередачі. Щоб запобігти зменшенню повздовжного вирівнювання концентрацій, застосовують різні технологічні методи (використання дрібної насадки, організація руху потоку і т.д.).

3.1.10 Конвективна дифузія

При потоці, що рухається, маса речовини переноситься як за рахунок молекулярної, так і за рахунок турбулентної дифузії. Загальний перенос речовини можна записати, як:

(3.70)

Сумарний перенос речовини називається конвективною дифузією. Переходячи до кінцевих різниць в виразі (3.70), одержимо:

(3.71)

З іншої сторони дифузійний потік із dM= К∆cdF запишеться як:

q = КΔс (3.72)

Прирівнявши праві частини виразів (3.71) і (3.72), одержимо:

(3.73)

Коефіцієнт масопередачі враховує перенос речовини, як за рахунок молекулярної, так і вихрової дифузії. Таким чином, механізм процесу масопередачі зводиться до молекулярної і конвективної дифузії. Структурна модель процесу масопередачі наведена на рис. 3.10.:

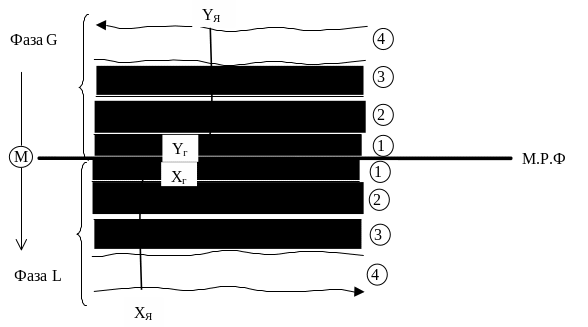
Рис. 3.10 Структурна модель процесу масопереносу.

1 – дифузійний прошарок;

2 – в’язкий прошарок;

3 –турбулентний пограничний шар;

4 – ядро потоку.

В ядрі потоку 4 маса цільового компоненту в основному переноситься потоком середовища за рахунок турбулентних пульсацій, молекулярна дифузія присутня, але її роль мінімальна.

З наближенням до дифузійного прошарку 1 перенос маси за рахунок турбулентної дифузії зменшується, і тому збільшується частка маси, перенесеної за рахунок молекулярної дифузії, але ще у в’язкому прошарку 2 основний перенос маси – турбулентний. В дифузійному прошарку маса переноситься в основному за рахунок молекулярної дифузії.

Концентрація цільового компонента в ядрі 4 потоку Y_Я постійна. Потім повільно зменшується в турбулентному прошарку 3. У дифузійному прошарку 1 суттєво зменшується. З’являється градієнт концентрацій і підвищується роль молекулярної дифузії.