3.1.6 Рівновага при масопередачі

3.1.6.1 Правило фаз

При масопередачі має місце наявність двох фаз. Цільовий компонент переходить з однієї фази до іншої до встановлення стану рівноваги.

Кінець процесу масопередачі (теоретичний) визначається станом рівноваги, який залежить від умов проведення процесу – температури, і тиску. Умови, при яких система знаходиться в стані рівноваги, можуть змінюватись.

Для визначення умов стану рівноваги застосовується правило фаз, яке визначає кількість параметрів N, які можна змінювати довільно, не порушуючи стану рівноваги в системі:

К + 2 = Ф + N (3.29)

де К – число компонентів системи;

Ф – число фаз;

N – число ступенів свободи (число змінних параметрів, які можна змінювати без порушення стану рівноваги).

Розглянемо деякі випадки:

1. Для води при t = 0,0075 С і Р = 6100 Па існують всі три фази, так звана потрійна точка. Для цього випадку число компонентів К = 1, число фаз Ф = 3, число ступенів свободи:

N = К + 2 – Ф = 1 + 2 – 3 = 0

Тобто не можна змінювати жодного параметра без порушення стану рівноваги.

2. Система вода – насичена пара: К = 1; Ф = 2. Число ступенів свободи:

N = К + 2 – Ф = 1 + 2 – 2 = 1

Одна ступінь свободи. Тобто не порушуючи стану рівноваги, можна змінювати або температуру, або тиск. Змінюючи температуру, змінюємо тиск, зберігаючи рівновагу в системі, тобто забезпечуючи існування як рідини, так і пари.

Для води широко застосовуються залежності Р = f(t) і t = f(P), які характеризують рівноважний стан системи і наведені в термодинамічних таблицях.

3. При масопередачі часто зустрічаються випадки, коли К = 3 (абсорбція) – цільовий компонент і два носії в двох фазах; і К = 2 (ректифікація) коли інертний носій відсутній. Число фаз в обох випадках Ф = 2.

Для цих випадків:

N₁ = 3 + 2 – 2 = 3

N₂ = 2 + 2 – 2 = 2

Тобто стан рівноваги може бути збережений при N₁ = 2 і N₂ = 3 параметрів. До цих параметрів відносяться: температура t, тиск Р та концентрація цільового компонента в одній із фаз у або х.

Таким чином при Р = const i t = const зберігається рівновага, тобто кожній концентрації в одній фазі відповідає рівновага в другій:

y^P = f(x) (3.30)

Зазвичай при проведенні процесів масопередачі підтримують постійним один із незалежних параметрів (Р = const) або (t = const). Якщо Р = const, то кожній температурі t буде відповідати цілком визначена концентрація х або у. І кожному значенню тиску (при t = const) відповідає певне значення х або у.

3.1.6.2 Криві рівноваги

Таким чином, умови існування стану рівноваги при масопередачі можна описати за допомогою залежностей тиск-концентрація: P = f(x) при t = const; температура-концентрація: t =f(x) при Р = const і концентрація в одній фазі – рівноважна концентрація в іншій – y^P = f(x). Ці залежності можуть бути виражені за допомогою фазових діаграм, рис. 1.2, 1.3.

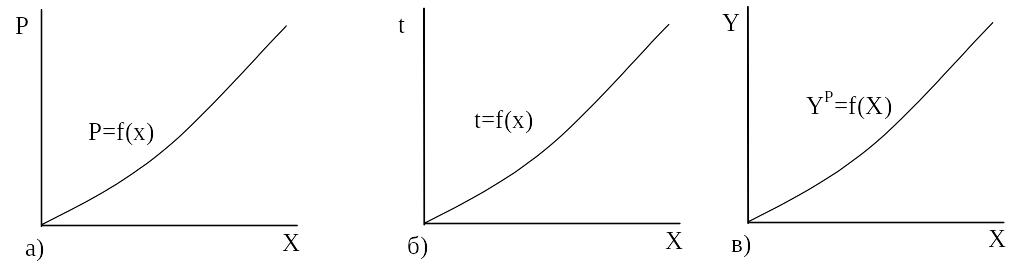
Рис. 3.2. Фазові діаграми рівноваги:

а) P = f(x) при t = const;

б) t =f(x) при Р = const;

в) y^P = f(x) при Р = const, t = const.

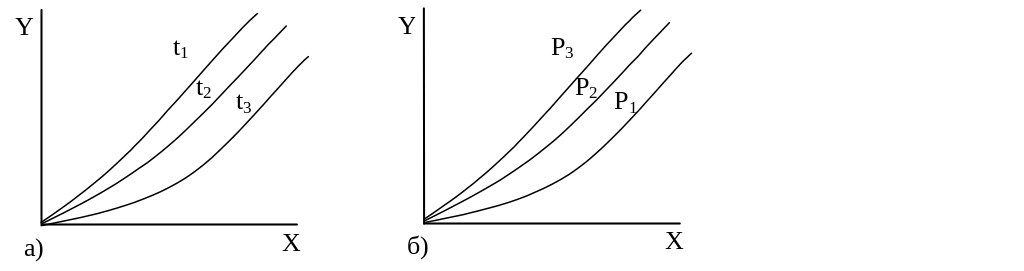Рис. 3.3. Залежність y^P = f(x) при різних значеннях температури і тиску:

а) y^P = f(x) при Р = const і t₁ > t₂ > t₃.

б) y^P = f(x) при t = const, і Р₁ > Р₂ > Р₃.

Криві рівноваги являють собою геометричне місце точок, які характеризують стан рівноваги між двома фазами Тобто, кожна точка на кривій рівноваги визначає кінцевий стан системи, або з точки зору технології, кінець процесу масопередачі на даній ділянці.

Найбільш поширена залежність, яка наведена на графіках

y^P = f(x) (3.31)

по яких, знаючи концентрацію в одній фазі х та умови проведення процесу – знаходять рівноважну концентрацію, а тому час перебігу процесу, розміри та об’єм апаратів.

Відношення концентрацій в двох фазах при рівновазі називається коефіцієнтом розподілення

(3.32)

і є тангенсом кута нахилу лінії рівноваги. Якщо лінія рівноваги крива, то m – величина змінна.

Для конкретних випадків масопередачі побудова ліній рівноваги проводиться на підставі законів, які характеризують цю рівновагу – закона Генрі і закона Рауля.