3.1.25 Методика розрахунку тарільчатого масообмінного апарата

1 Задаються:

Тип апарату, тип тарілки, витрати газової фази G, х_n, Y_n та Y_к - в газовій фазі, Х_n - в рідкій фазі, фізичні параметри суміші.

2. Із матеріального балансу задаємося Х_к, та розраховуємо витрати поглинача:

3. Визначаємо число дійсних тарілок за кінетичними кривими.

4. Розраховують діаметр апарату.

5. Визначаємо відстань між тарілками h

6. Обчислюємо висоту апарата: Н = N_дh.

7. Розраховуємо гідравлічний опір апарату:

, (3.155)

де гідравлічний опір барботажної тарілки складається з опору сухої тарілки Р_сух; опору, викликаного силами поверхневого натягу - Р_Г і опору шара рідини на тарілці - Р_p, де

3.1.26 Масопередача в системах з твердою фазою

Масопередача в системах з твердою фазою являє собою особливо складний процес. В цьому процесі, окрім масовіддачі від поверхні розділу фази в потік рідини (газу, пари), має місце і рух речовини в твердій фазі масопровідністю. До вказаних процесів потрібно віднести процеси адсорбції, сушки і екстракції (вилучення цільового компоненту з пор твердого тіла). Для цих процесів характерне зменшення швидкості переносу маси в порівнянні з швидкістю молекулярної дифузії. Тому в науково-технічній літературі при описі вказаних процесів користуються терміном "стіснена дифузія", що пояснюється механічним опором дифузійному потоку самим каркасом твердого пористого тіла і опором руху молекул.

Для опису дифузії в твердому середовищі запропоновано кінетичну характеристику - коефіцієнт масопровідності. Тоді в якості закону, якому підпорядкована кінетика переносу розподіленої речовини в твердому тілі, може бути прийнятий закон, аналогічний закону теплопроводності - кількість речовини, що перемістилась в твердій фазі за рахунок масопровідності, пропорційна градієнту концентрації, площі, перпендикулярної напряму потоку речовини, і часу:

(3.156)

В цьому рівнянні коефіцієнт пропорційності k називається коефіцієнтом масопровідності.

Процес переносу речовини всередині твердої фази може бути описаний диференціальним рівнянням масопровідності:

(3.157)

Коефіцієнт масопровідності не є сталою величиною. Він залежить від природи процесу, що відбувається (адсорбція, сушка, висолювання), від ряду факторів, які визначають величину коефіцієнта молекулярної дифузії, і від структури твердого пористого тіла.

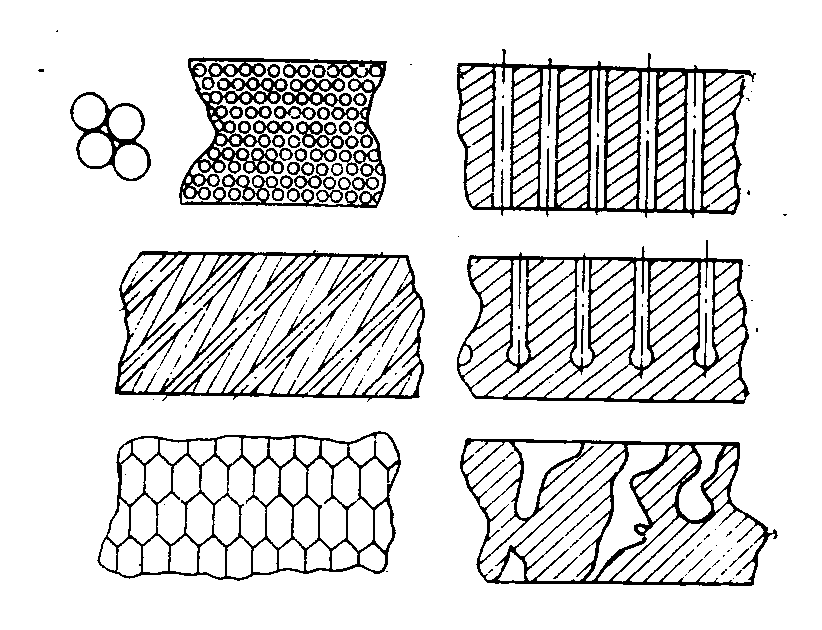
Рис. 3.35. Структурні модифікації пористих тіл.

На рис. 3.35. приведені типові структурні модифікації твердих пористих тіл. Ці модифікації наглядно показують, що у відношенні кінетики процесу різні структури нерівноцінні.

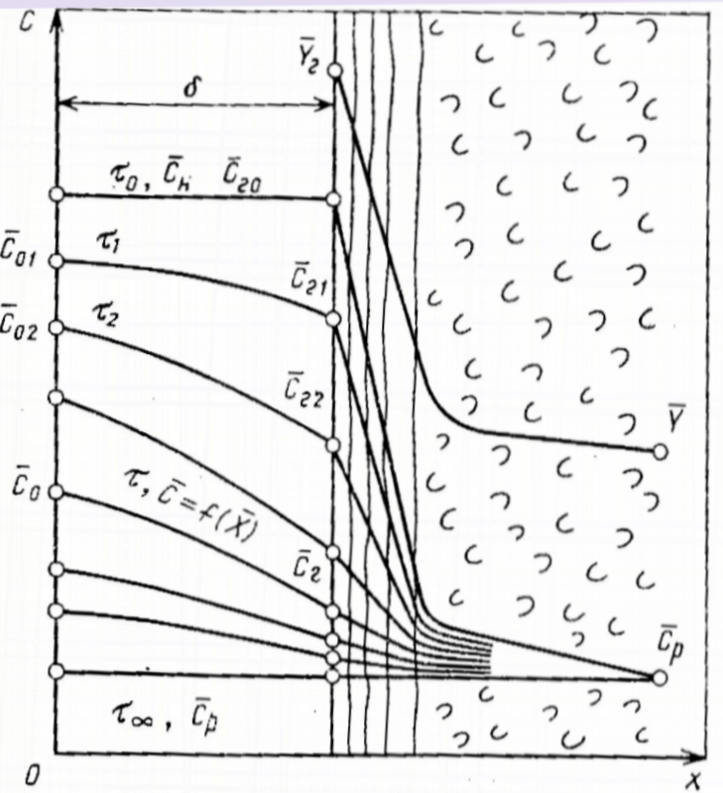
Рис. 3.36. Схема руху розподіленої речовини з твердої в рідку фазу.

Ідеалізована схема переносу речовини з твердої в рідку (газову, парову) фазу приведена на рис. 1.36. Тверда фаза являє собою необмежену пластину товщиною 2б. В початковий момент часу концентрація розподіленої речовини постійна по всьому об'єму пластини і дорівнює . Пластину з двох сторін омиває потік рухомої фази. Внаслідок симетрії системи розглядається процес, що відбувається тільки в одну сторону відносно осі симетрії пластини. Приймаємо, що в наведеному перерізу, перпендикулярному середній площині пластини і напряму потоку, концентрація розподіленої речовини в ядрі омиваючої фази постійна протягом всього процесу і дорівнює .

При передбачується, що залежність відома, розподілена речовина рухається із твердої фази в ядро омиваючої фази, причому від середньої площини пластини до поверхні речовина рухається масопровідністю, а від поверхні в ядро омиваючої фази - конвективною дифузією.

В початковий момент часу градієнт концентрації по товщині пластини і речовина починає рухатись в омиваючу фазу з твердої фази тільки із об'єму, що безпосередньо прилягає до поверхні розділу фаз. В омиваючій фазі концентрація змінюється від до , або від до . В наступні моменти часу внаслідок переходу речовини з твердої фази в омиваючу фазу по товщині пластини спостерігаються градієнти концентрацій і концентрації в твердій фазі змінюються відповідно від С₀₁ ,С₀₂,...., С₀ в середній площині до С_г1, С_г2,...., С_г, на границі розділу фаз, а в сприймаючій фазі від Y_г1, Y_г2,…, Y_г. до Y_р в ядрі потоку.

Граничне (мінімальне) значення концентрації в твердій фазі С_р відповідає часу

Як бачимо із розглянутої схеми, особливістю масопровідності є нестаціонарний процес масопереносу.

Для розв’язку задачі щодо переміщення речовини всередині твердої фази диференціальне рівняння масопровідності повинне бути доповнене рівнянням, на границі розділу твердої і рідкої (газової, парової) фаз.

До елементарної поверхні на межі розділу фаз підводиться речовина з твердої фази в кількості dM, яку можна визначити виходячи із закону масопровідності:

(3.158)

Від елементарної площини відводиться в омиваючу фазу та ж кількість речовини dМ, яку можна визначити виходячи із закону конвективної дифузії:

(3.159)

Прирівнюючи праві частини двох останніх рівнянь, отримуємо диференціальне рівняння, що характеризує умову на границі розділу фаз:

(3.160)

Із (3.106) і (3.107) можуть бути отримані критерії, що характеризують рух речовини всередині твердої фази. Із рівняння (3.108) отримуємо безрозмірний комплекс, діленням правої частини на ліву:

(3.161)

З якого отримуємо дифузійний критерій Ві_д:

диференціального рівняння масопровідності

для осі Х отримуємо безрозмірний комплекс, діленням правої частини на ліву:

З якого отримуємо дифузійний критерій Фурьє:

(3.162)

що характеризує зміну швидкості потоку речовини, яка рухається під дією масопровідності в твердому тілі.

Дифузійні критерії Ві_д і Fо_д повинні ввійти в критеріальне рівняння, що описує рух речовини в твердій фазі і є теоретичною базою для обробки всіх експериментальних досліджень цього процесу.

Диференціальне рівняння масопровідності для найпростіших випадків одномірного руху речовини має аналітичне вирішення у вигляді:

(3.163)

де - - параметричний критерій, який являє собою безрозмірну концентрацію розподіленої речовини в твердій фазі в точці з координатою х; концентрація в точці з координатою х в момент часу , що відповідає певному Fо_д;  - визначальний розмір тіла, що складає тверду фазу; х/ - безрозмірна координата точки, в якій концентрація дорівнює С.

У випадку, що розглядається, в момент часу  концентрація всередині пластини змінюється від С₀ до С_г , в залежності від координати х, .

Аналітичний розв’язок диференційного рівняння масопровідності у вигляді рівняння (3.159) існує для найпростіших тіл: необмеженої пластини, необмеженого циліндра та кулі. Функціональна залежність представлена у вигляді нескінченних рядів. Для спрощення розрахунків, що використовуються для трьох перших з перелічених тіл складають графіки, що дають можливість за критеріями Ві_д і Fо_д визначити для кожного тіла три рівняння, що являють собою найбільшу для практики цінність - безрозмірні концентрації:

(3.164)

(3.165)

(3.166)

де С₀ - концентрація в момент часу  в середній площині необменженої пластини (на необмеженого циліндрі, або в центрі кулі), С_гр – концентрація на поверхні твердого тіла, С_ср - середня для всього тіла концентрація.

Розв’язок (3.163)-(3.166) справедливий також і для випадків, коли розподілена речовина рухається із омиваючого потоку в тверде тіло, тобто, коли С _Н < С _Р .

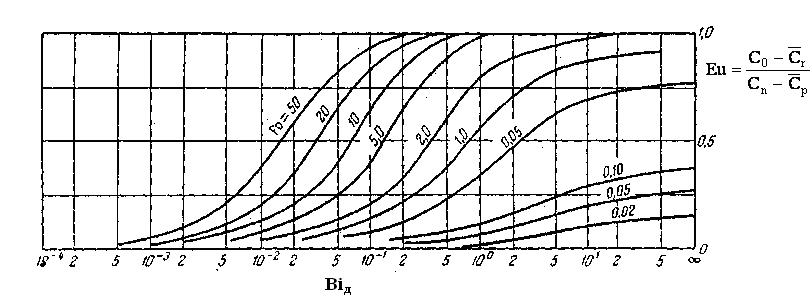
Рис. 3.37 Залежність Eu від Fo_д і Bi_д для кулі

На рис. 3.37 наведена залежність приведеної концентрації Eu від критерію Ві для різних значень критерія Фур’є.

Маючи таку залежність, розв’язують пряму та обернені задачі.

56