Тема 7. Логические основы теории аргументации.

1. Понятие аргументации и ее аспекты.

2. Доказательство, его структура и виды.

3. Правила и ошибки в доказательстве.

1.Понятие аргументации и ее аспекты.

Аргументация (лат.argumentatio -) – способ подведения оснований под какую-либо мысль или действие (обоснование) с целью их публичной защиты, побуждения к определенному мнению о них, признания или разъяснения;

- способ убеждения кого-либо посредством значимых аргументов.

В этом смысле аргументация всегда диалогична и шире логического доказательства, поскольку она ассимилирует не только «технику мышления» (собственно логику), но и «технику убеждения» (искусство подчинять мысль, чувства и волю человека).

Главные аспекты Аргументации:

1. фактуальный (информация о фактах, используемых в качестве аргументов);

2. риторический [< др. – греч. rhetorike] – наука об ораторском искусстве, о художественной прозе; теория, искусство красноречия] – (формы и стили речевого и эмоционального воздействия);

3. аксиологический (ценностный подбор аргументов);

4. этический (нравственная приемлемость или дозволенность аргументов);

5. логический (последовательность и связность аргументов, их организация в дедуктивный вывод).

Эти и другие аспекты аргументации рассчитаны на то, чтобы наилучшим образом повлиять на данную аудиторию. Поэтому они взаимодополняют друг друга:

- фактуальный аспект определяет «материю» аргументации, а остальные аспекты – ее форму, «форму сказывания».

Но их значимость может варьировать в зависимости от конкретной ситуации. Например, в обиходе чисто логические средства аргументации используются редко. В свою очередь, правильный логический вывод не зависит от убедительности посылок и аксиом. Его принудительность (обязательность, общезначимость) – во взаимной связи суждений по правилам вывода.

Если же при этом имеет место и убежденность в истинности суждений (посылок и аксиом); то логический довод становится логическим доказательством, т.е. объективно сильным вариантом аргументации (Филос. энциклопед. словарь. – М.: Сов. энц., 1989. – с. 36). Важнейшим элементом аргументации является доказательство…

2. Понятие доказательства: структура и виды

Проблема доказательства и его приемы были и остаются предметом внимания логиков со времени зарождения логики, т.к. достижение достоверного, истинного знания связано с доказательством.

Доказательство – это логическая операция, обосновывающая истинность какой-либо мысли с помощью других мыслей.

Многовековой опыт убедил людей в том, что доказательность является важным свойством правильного мышления. Еще Аристотель говорил, что люди тогда всего более в чем-нибудь убеждаются, когда им представляется что, что-либо доказано. Цицерон говорил, что сила доказательств выше всякого авторитета.

Всякое доказательство представляет свой вывод об истинности доказываемой мысли из других мыслей, признанных за истинные.

Это предполагает решение двух задач:

- 1) точно определить и правильно классифицировать формы отношений между мыслью доказываемой и мыслями, с помощью которых обосновывается истинность доказываемой мысли;

Дело в том, что вопрос о том, какую истинную по содержанию мысль надо взять в качестве посылки доказательства, логика не может указать. В каждом конкретном случае это определяется той или иной наукой. Например, хорошо или плохо знает логику физик, но чтобы доказать истинность тезиса о том, что волновая функция есть статистическая характеристика квантового ансамбля, а не отдельной частицы – физику надо знать истинные мысли из других областей физики (квантовой механики), из которых можно вывести истинность доказываемого тезиса.

Но вот вопрос о том, какую нужно взять мысль по форме – общее, частное или единичное суждение и какие логические формы связи и отношения использовать между известными истинами, взятыми в качестве доказательства и доказываемым тезисом - это решает логика.

- 2) выяснить, какие мысли являются уже доказанными и истинными, которые мы берем в качестве доказательства. Если мы не найдем такие истинные мысли, а возьмем мысли, которые сами требуют доказательства, то этот процесс может быть долгим. Поэтому нужно брать такие истинные мысли, которые в обосновании не нуждаются.

Несмотря на то, что каждая наука использует свои методы и факты, логика нашла то общее, что характерно для всех доказательств. Знание того общего, что лежит в основе связи и сочетания мыслей в процессе доказательства, позволило логике сформулировать структурные элементы доказательства и правила.

Общим для всех доказательств являются следующие элементы, образующие логическую последовательность:

- 1) структура доказательства,

- 2) способ доказательства,

- 3) общие требования в отношении доказываемой мысли,

- 4) и требования в отношении мыслей, с помощью которых обосновывается доказываемое положение.

Структура доказательства. Всякое доказательство состоит из трех взаимосвязанных частей: тезиса; аргументов (доводов или оснований) и демонстрации.

Структуру доказательства можно представить в виде след. схемы:

тезис

демонстрация

аргумент

а₁ а₂ ... а_n

Тезис (греч. слово – положение, утверждение) – это мысль или положение, истинность или ложность которого (выясняется) обосновывается в процессе доказательства.

В качестве тезиса могут быть:

- теоретическое положение науки,

- теорема в математике,

- результаты опытного исследования, которые нужно обобщить,

- причина того или иного явления или события,

- диагноз заболевания,

- выяснение конкретного исторического факта и т.д.

Доказательство будет успешным лишь в том случае, если доказываемый тезис истинен по своему содержанию.

Аргументы. Доказательство осуществляется при помощи аргументов (доводов или оснований).

Аргументы (лат. argumentum – логический довод, основание доказательства) – это истинные исходные теоретические или фактические положения, на которые опирается доказательство и из которых необходимо следует истинность доказываемого тезиса.

Аргументами могут быть: аксиомы, принятые в данной научной системе, определения, суждения о достоверно известных фактах; теоретические или опытные обобщения и т.п.

Так, при доказательстве некоторого суждения аргумент является основанием, из которого логически следует доказываемое суждение. Например, нам нужно доказать, что железо проводит электрический ток. Для этого достаточно двух аргументов:

1. «Все металлы проводят электрический ток.

2. Железо – металл».

Следовательно, железо проводит электрический ток.

Демонстрация – (от лат. demonstratio – показывание).

Истинность доказываемого тезиса не дана непосредственно, она не очевидна. Поэтому необходимо показать какова связь, которая ведет от истинности данных оснований к истинности тезиса. Эта связь требует выяснения.

Положим, что ученик знает все определения, аксиомы и все теоремы, из истинности которых как из оснований выводится истинность теоремы Пифагора. Но это еще не значит, что он знает доказательство теоремы Пифагора.

Чтобы знать доказательство необходимо:

- знать какова связь между всеми основаниями теоремы Пифагора;

- знать последовательность оснований и выводов из них, которая ведет к признанию истинности доказываемого в этой теореме положения.

Таким образом, демонстрация – это логическая связь между аргументами и тезисом, выраженная в форме логического рассуждения, в ходе которого из аргументов выводится истинность тезиса.

Демонстрация отличается от тезиса и аргументов. Если тезис и аргументы могут быть представлены в виде отдельных суждений, то демонстрация – это более или менее длинная цепь суждений и умозаключений, посылками которых являются аргументы, а заключением – тезис.

Продемонстрировать – это значит при помощи логических рассуждений доказать, что тезис логически следует из взятых нами аргументов по правилам соответствующих умозаключений.

Обоснование тезиса может протекать в различной форме. Оно зависит от содержания и характера доказательства. Обоснование может иметь форму дедуктивных умозаключений, индуктивных умозаключений и умозаключений по аналогии.

Виды доказательства. Различают прямое и косвенное доказательство. При прямом доказательстве истинность тезиса непосредственно обосновывается аргументами. Из аргументов а, в, с – с необходимостью следует доказываемый тезис d. Логическая формула прямого доказательства такова: 1) Из множества аргументов α выводим тезис β. 2) Множество аргументов α - истинно. 3) Тезис β - истинный

1. Все углеводы горючие

2. Сахар - углевод

Сахар - горюч.

Косвенное (непрямое) доказательство. Здесь истинность выдвинутого тезиса обосновывается путем доказательства ложности антитезиса. Оно имеет два варианта: а) апагогическое (от греч. apagõg s – уводящий). – это доказательство, когда мы допускаем истинность противоречащего суждения, т.е. истинность антитезиса. Это так называемое доказательство от противного. При этом допускается временно истинность противоречащего суждения, из которого выводят следствия, в результате чего мы приходим к противоречию. На этом основании делается заключение, что противоречащее суждение ложно, и, следовательно, истинно доказываемое суждение.

Допустим, что нам требуется доказать суждение А. Допускаем не-А, из него выводим следствие В, приводящее нас к противоречию. Следовательно, В является ложным. Тогда наше предположение, что из не-А следует В (не-А→В) может быть истинным только, если не-А является ложным. Следовательно А является истинным. Совершая переход от ложности не-А к истинности А, мы используем закон исключенного третьего.

Разделительное доказательство. Это доказательство методом исключения. В этом доказательстве антитезис является одним из членов разделительного суждения, в котором нужно перечислить все возможные альтернативы. Например, нужно доказать, что проступок совершил Петров. Берем дизъюнктивное суждение: «Этот проступок совершил Иванов или Сидоров, или Петров». При доказательстве выясняется, что Иванов этот проступок не совершал, Сидоров также этот проступок не совершал. Их мы исключаем и получаем заключение: «Проступок совершил Петров».

Опровержение (лат. refutation – доказательство ложности или неправильности выдвинутых утверждений, предложений и доказательств).

Обычно опровергают доказательства. Это более важный вид опровержения. Это можно сделать в отношении всех структурных элементов доказательства:

- опровергнуть тезис;

- опровергнуть аргументы;

- опровергнуть способ доказательства.

1) Чтобы опровергнуть тезис, нужно доказать его ложность или доказать антитезис.

Тезис: «все растения зеленые». Достаточно указать, что есть растения с розовыми листьями, желтыми, многоцветными.

2) Чтобы опровергнуть аргументы, мы используем тот же прием. Пример. «Земля имеет форму шара». Приводят аргумент: «Это доказывается кругосветным путешествием».

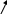
Н о! Этот аргумент сомнителен. Говорят, что выйдя из точки А и двигаясь по одному и тому же меридиану, можно вернуться к точке А. Но это можно сделать и тогда, когда Земля не круглая (см. рис.).

А

К

3. Правила и ошибки в доказательстве.

Значение этих правил в том, что они помогают твердо обосновывать наши знания; помогают разоблачать ложные приемы доказательства.

Существуют след. правила доказательства:

1) доказываемый тезис должен быть определен ясно и четно;

2) в процессе доказательства нельзя подменять тезис;

3) используемые в доказательстве аргументы должны быть истинными;

4) аргументы должны быть достаточными для обоснования тезиса;

5) аргументы должны быть такими суждениями, истинность которых доказана независимо от тезиса;

6) тезисом должно быть такое выводное суждение, которое логически следует из аргументов. Тезис – это суждение логически следующее из аргументов.

Эти правила ясны и понятны и не требуют особых комментариев. Но ложные приемы доказательства, играющие большую роль в таких науках как философия, политическая экономия, история, социология, психология и, особенно, в политической жизни и идеологии, следует рассмотреть. Здесь часто используются софизмы – вид ложного доказательства. Их цель – представить обманные утверждения как истинные, а истинные – как ложные.

При ложном доказательстве речь идет не столько об ошибках, сколько об обманных приемах. Защищают ложный тезис при помощи ложного доказательства не потому, что не знают правил доказательства, а потому, что в этом заинтересованы.

Уже Аристотель знал об этом и сформулировал правила доказательства и указал почти все ошибки.

Умение разоблачать ложные доказательства важно не потому, что это удержит софистов или лжецов, а потому, что оно научит нас разоблачать демагогов¹, софистов, политических авантюристов и т.п.

Типы ложного доказательства, встречающиеся в научных, идеологических и политических доказательствах:

1. Подмена доказываемого тезиса - это ошибка в доказательстве в результате нарушения закона тождества. Начав доказывать один тезис, в ходе доказательства переходят к доказательству другого тезиса, который внешне сходный с первым. Например, начав доказывать что-то несправедливое в моральном смысле, доказывают, что это несправедливо в юридическом смысле.

2. Доказательство через доказываемое, или круг в доказательстве (то же, через то же). Например, тезис А доказывается тезисом В и, одновременно В доказывается через А. Так, чтобы доказать тезис о том, что «человек разумное животное», ссылаются на то, что он может рассуждать, а рассуждать он может потому, что он разумен.

3. Учетверение термина. Это ошибка в умозаключении (в силлогизме). Известно, что в умозаключении должно быть три термина, а не четыре. Появление четвертого термина происходит от того, что употребляют многозначное слово. Пример:

1. Все металлы элементы

2. Латунь - металл

След., латунь - элемент