- •Лабораторна робота № 1 Розрахунок електричних кіл у застосунку MathCad
- •Програма роботи:
- •Методичні вказівки
- •Лабораторна робота № 2 Дослідження характеристик лінійних сак за їх передатними функціями
- •Програма роботи:
- •Методичні вказівки
- •Завдання
- •Лабораторна робота № 3 Розрахунок перехідних процесів електричних систем
- •Програма роботи:
- •Технічні дані двигунів постійного струму з незалежним збудженням серії 2п до задачі 2
- •Методичні вказівки
- •Лабораторна робота № 4 Основи роботи в застосунку matlab. Застосування пакету Control System для розрахунку частотних характеристик і динаміки системи
- •Програма роботи:
- •Методичні вказівки
- •Лабораторна робота № 5 Основи роботи в Simulink і SimPowerSystems
- •Програма роботи:
- •Методичні вказівки
- •Контрольна (розрахункова) робота з курсу “Прикладне програмне забезпечення в інженерній справі”
- •Методичні вказівки
Методичні вказівки
До п. 1
Для побудови аналітичним методом перехідного процесу за нульових початкових умов для електричного кола необхідно скласти рівняння рівноваги в операторній формі, після чого знаходять вираз для шуканої координати. Далі для цього виразу за допомогою зворотного перетворення Лапласа знаходять часові характеристики.
Використання перетворення Лапласа для побудови перехідного процесу за нульових початкових умов показано на прикладі електричного кола (рис. 3.2) для таких його параметрів: E = 300 B; R1 = 10 Ом; R2 = 15 Ом; R3 = 20 Ом; L1 = 25 мГн; L2 = 1.5 Гн; C = 68 мкФ.

Рис. 3.2. Схема електричного кола для прикладу
Паралельне з'єднання двох ланок з
послідовно увімкненими елементами
R2–L2
і R3–C
матиме імпеданс
 .
Відображення за Лапласом подачі (стрибка)
напруги E у момент
часу t = 0 с має вигляд
.
Відображення за Лапласом подачі (стрибка)
напруги E у момент
часу t = 0 с має вигляд
![]() ,
а відображення за Лапласом струму I1(s)
в цьому разі описують виразом
,
а відображення за Лапласом струму I1(s)
в цьому разі описують виразом
 .
.
Відображення напруги на паралельному
з'єднанні ланок R2–L2
і R3–C
знаходять з виразу
![]() ,
що дає змогу знайти відображення за
Лапласом струму через конденсатор
,
що дає змогу знайти відображення за
Лапласом струму через конденсатор
 .
Відображення шуканої напруги на
конденсаторі UC(s)
матиме вигляд
.
Відображення шуканої напруги на
конденсаторі UC(s)
матиме вигляд
![]() ,
з якого шляхом зворотного перетворення
Лапласа знаходять часову залежність
UC(t).
Приклад знаходження таким шляхом напруги
на конденсаторі показано нижче
(використано MathCAD версії
13).
,
з якого шляхом зворотного перетворення
Лапласа знаходять часову залежність
UC(t).
Приклад знаходження таким шляхом напруги
на конденсаторі показано нижче
(використано MathCAD версії
13).
Знаходження відображення струму I1
Знаходження відображення струму IС
Знаходження відображення шуканої напруги на конденсаторі
Отримання часової залежності за допомогою зворотного перетворення Лапласа
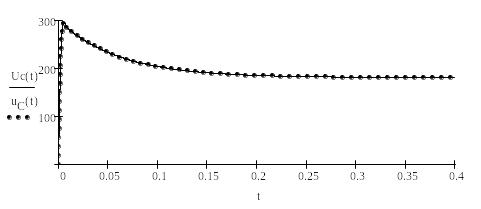
Побудова графіка часової залежності для напруги на конденсаторі
|
Для використання числових методів електричне коло, показане на рис. 3.2, потрібно описати системою диференціальних рівнянь:
![]()
Найпростішим способом розв'язування такої системи диференціальних рівнянь є використання блоку Given … Odesolve, що показано на прикладі нижче.
Given
Виведення на один графік аналітичного і числового розв'язків
|
Для розв'язування даної системи диференціальних рівнянь рекомендується використання адаптивного методу (adaptive – вибирається натисканням на ключовому слові Odesolve правої кнопки мишки) – див. далі.
До п. 2
Передатна функція двигуна постійного струму визначається з його структурної моделі (рис. 3.3) шляхом аналітичних перетворень для замкненої структурної моделі:
передатна функція за струмом:
 ;
;передатна функція за швидкістю:
 ,
,
де
![]() ;
;![]() ;
;
![]() ;
;
![]() ;
;
![]() (нижній індекс "ном" біля величин
означає номінальне значення).
(нижній індекс "ном" біля величин
означає номінальне значення).

Рис. 3.3. Структурна модель двигуна постійного струму
Прямий пуск двигуна (відповідає перехідній характеристиці для величини стрибка напруги на якорі Uн) буде описуватися в операторній формі виразами:
за струмом – ![]() ;
;
за швидкістю – ![]() .
.
За виразами в операторній формі за допомогою зворотного перетворення Лапласа з використанням засобів символьної математики знаходять з точністю 3-4 значущих цифр часові функції струму якоря та швидкості (див. методичні вказівки до лабораторної роботи № 2). Залежності струму якоря ia(t) і частоти обертання ω(t), розраховані за відповідними формулами, вивести на екран у вигляді графіків. Часовий проміжок [0; Tmax] вибрати достатнім для відображення всього процесу пуску.
Іншим способом часових знаходження залежностей струму якоря ia(t) і частоти обертання ω(t) є опис динаміки двигуна системою звичайних диференціальних рівнянь з наступним їх розв'язуванням числовим методом засобами MathCAD.
Для розв'язування звичайних диференціальних рівнянь у MathCAD версії 13 передбачено декілька вбудованих функцій, зокрема:
rkfixed – функція призначена для розв’язування звичайних диференціальних рівнянь та системи з n диференціальних рівнянь за допомогою формули Рунґе-Кутта четвертого порядку з фіксованим кроком і є базовою в пакеті. Виклик функції:
rkfixed(y, Xmin, Xmax, Npoints, D), де
y – вектор початкових умов у точці Xmin розміром n ;
Xmin, Xmax – початкова і кінцева точки інтервалу інтегрування;
Npoints – бажана кількість точок розв’язку на інтервалі інтегрування, визначає 1+Npoints рядків результуючої матриці, яку повертає функція rkfixed; для стійкого розв’язку і достатньої для інженерних розрахунків точності потрібно подбати, щоби значення кроку інтегрування не перевищувало значення найменшої сталої часу;
D – функція-вектор, що містить перші похідні шуканої функції, складається з n рядків;
rkfixed повертає результуючу матрицю (для прикладу назвемо її S), в якій:
перший стовпець S<0> містить значення аргументу в точках розв’язку;
наступні стовпці містять розв’язки за кожною змінною: наприклад, перший стовпець S<1> містить (1+Npoints)-елементний вектор розв’язку першої змінної, S<2> – вектор розв’язку другої змінної і т. д., відповідно, S<n> містить вектор розв’язку n-ої змінної.
Rkadapt – функція для розв’язування нежорстких систем з розв’язком, який змінюється повільно (є досить універсальною, тому її можна використовувати у багатьох випадках), використовує алгоритм з автоматичним вибором кроку інтегрування на основі формули Рунґе-Кутта четвертого порядку, але результат подається у рівновіддалених точках (як у rkfixed); функція викликається аналогічно.
Bulstoer – реалізація методу Булірш-Штура (Bulirsch-Stoer) для розв’язування гладких функцій, для яких є дещо точнішою, ніж метод Рунґе-Кутта, що реалізований в rkfixed; викликається так само, як і попередні функції.
Stiffb – функція для розв’язування системи жорстких диференціальних рівнянь, застосовує метод Булірш-Штура.
Stiffr – функція для розв’язування системи жорстких диференціальних рівнянь, застосовує метод Розенброка (Rosenbrock); обидві функції викликаються подібно:
Stiffb(y, Xmin, Xmax, Npoints, D, J)
Stiffr(y, Xmin, Xmax, Npoints, D, J), де
J – функція, що повертає матрицю розміром n(n+1), в якій перший стовпець містить похідні, а наступні стовпці складають матрицю Якобі системи диференціальних рівнянь.
У MathCAD версії 15 додано функції:
Adams – реалізація методу Адамса для нежорстких систем диференціальних рівнянь.
Radau – реалізація методу Radau5 (автори E. Hairer і G. Wanner, реалізує неявний метод Рунґе-Кутта 5-го порядку з автоматичним вибором кроку розв'язування) для жорстких систем диференціальних рівнянь.
BDF – реалізація методу ФДН (формул диференціювання назад) для жорстких систем диференціальних рівнянь.
AdamsBDF – реалізація комбінованого методу Адамса/ФДН для будь-яких систем диференціальних рівнянь (метод вибирається автоматично).
Використання функцій розв’язування системи диференціальних рівнянь застосунку MathCAD показано на прикладі: задано систему диференціальних рівнянь, що описує пуск двигуна постійного струму зі сталим потоком збудження.
![]()
Приклад розв’язування цієї системи з використанням функцій розв'язування звичайних диференціальних рівнянь (у прикладі використано функцію rkfixed) і функції-вектора правих частин системи диференціальних рівнянь, записаної у нормальній формі Коші, показано нижче в документі MathCAD.
N : = 100 кількість точок розв’язку tmin : = 0 tmax : = 1 межі (діапазон) інтегрування y0 : = 0 y1 : = 0 початкові умови диференціального рівняння Задаємо параметри двигуна: Ta : = 0.05 Стала часу якірного кола Ua : = 50 Напруга на якорі C : = 2.5 Стала двигуна Ra : = 0.1 Опір якірного кола J : = 2 Момент інерції приводу Ic : = 0 Статичний струм
Отримуємо розв’язок і виводимо на графік: S : = rkfixed(y, tmin , tmax , N , DiffEq)
( Для даного двигуна масштаб швидкості збільшено у 10 разів лише для наочності ) |
У випадку версії не нижче MathCAD 11 (а краще MathCAD 13 і вище) можливий варіант документа зі зрозумілішою формою запису системи диференціальних рівнянь із застосуванням конструкції Given … Odesolve. Диференціальні рівняння повинні бути лінійні відносно найстаршої похідної. Функцію в кінці блоку записуємо так
Odesolve(V, x, Xmax[, N])
де V (записують тільки для систем) – вектор, у якому перелічені імена функцій, стосовно яких розв’язується система рівнянь. Для назв функцій не допускається використовувати елементи масивів;
x – змінна, за якою здійснюється інтегрування;
Xmax – кінцеве значення змінної інтегрування. Ця величина повинна бути більшою за початкове значення змінної інтегрування, яке задається у початкових умовах у межах блоку розв’язування рівнянь;
N (необов'язковий параметр) – ціле число кроків, яке використовують під час інтерполяції розв’язку з апроксимованих точок. За замовчуванням приймається 1000.
У результаті розрахунку повертаються функції, які є розв’язками заданої у блоці розв’язування системи звичайних диференціальних рівнянь, і відповідають встановленим початковим або граничним умовам, а також обмеженням. Кількість початкових та обмежуючих умов повинна відповідати порядкові системи.
Встановивши курсор на функції Odesolve і натискаючи праву кнопку миші, викликають допоміжне підменю, в якому можна вибрати алгоритм розв’язування (показано для версії 13 застосунку MathCAD):
fixed – з фіксованим кроком (діє за замовчуванням);
adaptive – адаптивний (автоматичний вибір кроку);
stiff – для жорстких систем звичайних диференціальних рівнянь.
Для версії 15 застосунку MathCAD набір можливих методів змінено:
 Adams/BDF
– метод використовується за замовчуванням,
здійснює динамічне перемикання між
методами Адамса (для нежорстких задач)
і ФДН (для жорстких задач) з адаптацією
кроку розв'язування до поведінки
функції;
Adams/BDF
– метод використовується за замовчуванням,
здійснює динамічне перемикання між
методами Адамса (для нежорстких задач)
і ФДН (для жорстких задач) з адаптацією
кроку розв'язування до поведінки
функції;Fixed – з фіксованим кроком (реалізовано метод Рунґе-Кутта);
Adaptive – адаптивний (реалізовано метод Рунґе-Кутта з автоматичним вибором кроку);
Radau – для жорстких систем звичайних диференціальних рівнянь.
Під час запису диференціальних рівнянь у такому блоці необхідно пам'ятати таке:
Невідомі функції повинні бути записані явно через змінну інтегрування, тобто f(x), а не просто f.
Рівняння записують з використанням знаку "символьне дорівнює", який набирається комбінацією клавіш Ctrl + = (дорівнює) або натисканням кнопки
 .
.Похідна у рівняннях позначається через символ похідної d/dx, який викликається з підменю або комбінацією клавіш Shift + / , або через символ ' , який викликається комбінацією Ctrl + F7.
Початкові та граничні умови записуються так само всередині блоку Given … Odesolve, подібно до рівнянь системи. Кінцеве значення змінної інтегрування, задане в граничній умові, має збігатись з кінцевим значенням в Odesolve.
Допускаються алгебричні обмеження виду f(b) + g(b) = h(b). У такому випадку функція h має бути перелічена у векторі v, який задається у функції Odesolve.
У блоці Given … Odesolve не допускається використання:
операцій присвоєння : = ;
нерівностей як обмежуючих умов;
елементів програмування;
діапазонних змінних;
інших блоків розв'язування.
h : = 0.005 Крок розв’язку tmin : = 0 tmax : = 1 Межі (діапазон) інтегрування Ia0 : = 0 0 : = 0 Початкові умови Задаємо параметри двигуна: Ta : = 0.05 Стала часу якірного кола Ua : = 50 Напруга на якорі C : = 2.5 Стала двигуна Ra : = 0.1 Опір якірного кола J : = 2 Момент інерції приводу Ic : = 0 Статичний струм Задаємо систему диференціальних рівнянь Given
Ia(0) ═ 0 (0) ═ 0
Отримуємо розв’язок і виводимо на графік: t : = tmin , tmin + h .. tmax
( Для даного двигуна масштаб швидкості збільшено у 10 разів лише для наочності) |
Знайти перевищення пускового струму
двигуна відносно номінального під час
прямого пуску найпростіше за допомогою
аналізу графіка модуля відношення
знайденого пускового струму до
номінального:
![]() .
Під час формулювання висновків про
допустимість режиму прямого пуску
двигуна постійного струму врахувати,
що з умов комутації струм якоря не
повинен перевищувати 2.5Iном .
.
Під час формулювання висновків про
допустимість режиму прямого пуску
двигуна постійного струму врахувати,
що з умов комутації струм якоря не
повинен перевищувати 2.5Iном .


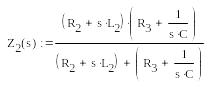

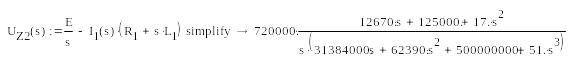


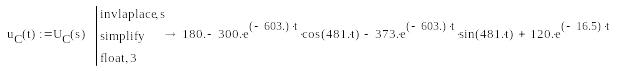


 задаємо
функцію-вектор для обчислення похідних
задаємо
функцію-вектор для обчислення похідних