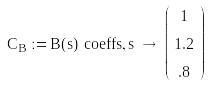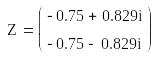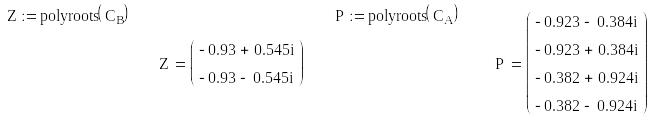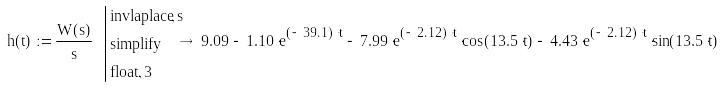- •Лабораторна робота № 1 Розрахунок електричних кіл у застосунку MathCad
- •Програма роботи:
- •Методичні вказівки
- •Лабораторна робота № 2 Дослідження характеристик лінійних сак за їх передатними функціями
- •Програма роботи:
- •Методичні вказівки
- •Завдання
- •Лабораторна робота № 3 Розрахунок перехідних процесів електричних систем
- •Програма роботи:
- •Технічні дані двигунів постійного струму з незалежним збудженням серії 2п до задачі 2
- •Методичні вказівки
- •Лабораторна робота № 4 Основи роботи в застосунку matlab. Застосування пакету Control System для розрахунку частотних характеристик і динаміки системи
- •Програма роботи:
- •Методичні вказівки
- •Лабораторна робота № 5 Основи роботи в Simulink і SimPowerSystems
- •Програма роботи:
- •Методичні вказівки
- •Контрольна (розрахункова) робота з курсу “Прикладне програмне забезпечення в інженерній справі”
- •Методичні вказівки
Лабораторна робота № 2 Дослідження характеристик лінійних сак за їх передатними функціями
Мета роботи: навчитись будувати за передатними функціями графіки частотних і перехідних характеристик лінійних систем автоматичного керування (САК), знаходити розміщення нулів та полюсів передатної функції САК.
Програма роботи:
Згідно свого варіанту завдання побудувати за передатною функцією W(s):
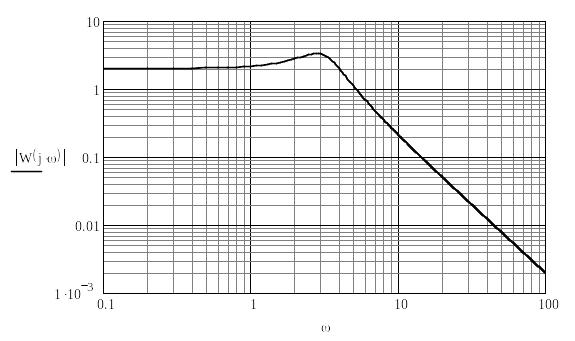
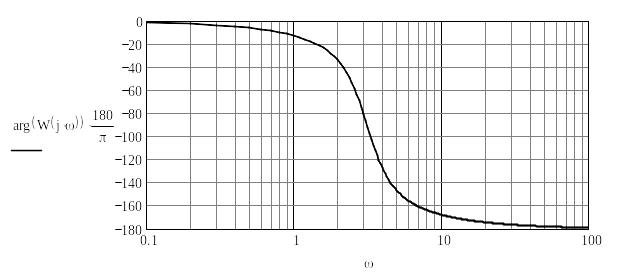
логарифмічні амплітудно-частотні (ЛАЧХ) і фазно-частотні (ФЧХ) характеристики САК (діаграми Бодé);
амплітудно-фазно-частотні (АФЧХ) характеристики САК (діаграму Найквіста).
Знайти нулі та корені передатної функції W(s) заданої САК і показати їх на комплексній площині.
За допомогою зворотного перетворення Лапласа і засобів символьної математики побудувати перехідну характеристику САК.
|
Пп. 1 і 3 виконати для двох випадків: заданого варіантом чисельника B(s) і для чисельника, що дорівнює одиниці (B(s) = 1), для аналізу впливу чисельника передатної функції на форму частотної та перехідної характеристик. |
Зробити висновки про досліджувану САК і вплив на її поведінку чисельника передатної функції.
Оформити звіт з роботи у вигляді документа MathCAD.
|
У звіті про виконану роботу подати:
|
Методичні вказівки
Дослідження частотних характеристик системи автоматичного керування (САК) є традиційним методом класичної теорії автоматичного керування (ТАК), яка базується на апараті передатних функцій і застосовує для їхнього аналізу перетворення Лапласа. Використання сучасних математичних застосунків, зокрема, MathCAD, дає змогу значно спростити цей аналіз і зробити процес досліджень легким і зрозумілим.
До п. 1.
Для
виведення ЛАЧХ/ФЧХ системи автоматичного
керування у застосунку MathCAD потрібно
задати дві передатні функції САК – з
чисельником, що дорівнює одиниці, та
чисельником, що заданий поліномом B(s):
![]() і
і
![]() .
Для зручності розв'язування задачі
поліноми чисельника B(s) і
знаменника A(s) передатної функції
доцільно описувати окремо. Також для
виведення графіків частотних характеристик
потрібно:
.
Для зручності розв'язування задачі
поліноми чисельника B(s) і
знаменника A(s) передатної функції
доцільно описувати окремо. Також для
виведення графіків частотних характеристик
потрібно:
задати зміну вхідної частоти (наприклад, як діапазонну змінну: : = 0, 0.01 .. 100 ) для наочного відображення частотних характеристик як у нижньому діапазоні частот, так і у верхньому діапазоні;
створити дві "заготовки" графіків вибором мишкою кнопки
 або натисканням на клавіатурі символів
@ , у які потім внести:
або натисканням на клавіатурі символів
@ , у які потім внести:
як аргумент за віссю X – кутову частоту (на обох графіках задати логарифмічний масштаб);
як функцію за віссю Y (див. приклад нижче):
на першому графіку (ЛАЧХ) – модулі обох комплексних передатних функцій
 і
і
 ,
які у полі графіка набирають через
кому і для яких задають логарифмічний
масштаб;
,
які у полі графіка набирають через
кому і для яких задають логарифмічний
масштаб;на другому графіку (ФЧХ) – за допомогою вбудованої функції кута комплексної змінної arg задають фази обох комплексних передатних функцій
 і
і
 ,
що у полі графіка набирають через кому;
для осі фаз залишають без змін лінійний
масштаб, для осі кутової частоти –
логарифмічний.
,
що у полі графіка набирають через кому;
для осі фаз залишають без змін лінійний
масштаб, для осі кутової частоти –
логарифмічний.
Для задавання логарифмічного масштабу осей координат (крім осі фази на другому графіку (графік ФЧХ), яка задається в лінійному масштабі) необхідно скористатись діалоговим вікном для форматування графіка (викликається подвійним клацанням лівої кнопки "мишки" на полі графіка), у якому увімкнути режим Log scale для потрібної координати. Для зручності читання інформації з побудованих графіків доцільно нанести лінії сітки, для цього на панелі форматування графіка увімкнути режим Grid lines, як показано нижче. Також не варто експериментувати зі стилем осей координат (Axis Style) і залишити їх за замовчуванням (Boxed), бо саме так прийнято в техніці для частотних характеристик.
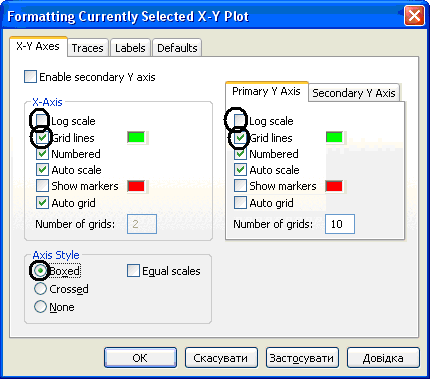
Змінити тип ліній графіка на бажаний (наприклад, для виведення результатів на чорно-білу друкарку) можна за допомогою вибору другої закладки меню форматування (Traces), що дає змогу зробити графік виразнішим.

Нижче показано приклад документу MathCAD для побудови ЛАЧХ і ФЧХ САК другого порядку за її передатною функцією (звернути увагу на правила запису уявної одиниці в MathCAD*)). Під час виклику передатної функції W(s) для побудови графіків потрібно замінити оператор Лапласа s на комплексну частоту j∙ (див. приклад).
Задаємо передатну функцію: Задаємо діапазон зміни частоти: : = 0, 0.01 .. 100
|
Досить часто трапляється, що передатна
функція САК є високого порядку (четвертого
і вище). У цьому разі безпосереднє
використання функції визначення кута
комплексної змінної arg призводить
до появи розривів на графіку фазної
частотної характеристики, тому що
функція арктангенса, яка використовується
функцією arg, визначена лише в діапазоні
від – до
рад. (–180º … 180º), що показано далі
в прикладі побудови в середовищі MathCAD
ЛАЧХ і ФЧХ системи автоматичного
керування шостого порядку з передатною
функцією
![]() .
.
Задаємо передатну функцію:
Задаємо діапазон зміни частоти: : = 0, 0.1 .. 100
|
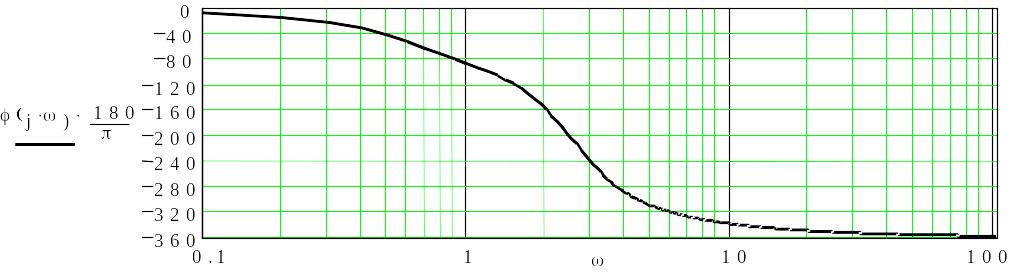
Зрозуміло, що отриманий графік ФЧХ з таким "стрибком" є некоректним, бо не відображає справжньої залежності. Виходом з цього положення є знаходження ФЧХ для кожного нуля (тобто, кореня чисельника передатної функції) і кожного полюса (тобто, кореня знаменника або, як ще його називають, характеристичного полінома) передатної функції САК окремо, бо вони гарантовано містяться в діапазоні від –/2 до /2 рад., а потім – обчислення їхньої суми, тобто знаходити фазну характеристику за формулою
![]() ,
,
де M – число нулів передатної функції;
N – число полюсів передатної функції;
Zi – i-ий нуль передатної функції;
Pk – k-ий полюс передатної функції;
j∙ – комплексна частота.
Під час реалізації даної формули в середовищі MathCAD потрібно врахувати, що нумерація індексів масивів починається з нуля. Приклад знаходження ФЧХ за цим методом подано нижче.
|
Частотний діапазон вибрати достатнім для відображення всіх змін фазної характеристики на графіку. |
Приклад: Побудувати графіки ЛАЧХ і
ФЧХ САК шостого порядку з передатною
функцією
![]() .
.
Задаємо чисельник передатної функції:
Задаємо знаменник передатної функції:
Задаємо передатну функцію: Задаємо діапазон зміни частоти: : = 0, 0.01 .. 100 Знаходимо коефіцієнти чисельника передатної функції:
Знаходимо нулі передатної функції: Z : = polyroots(CB)
Знаходимо коефіцієнти знаменника передатної функції:
Знаходимо полюси передатної функції: P : = polyroots(CA)
Число нулів M і число полюсів N передатної функції САК
Задаємо формулу для знаходження фазної частотної характеристики
Будуємо фазну частотну характеристику
|
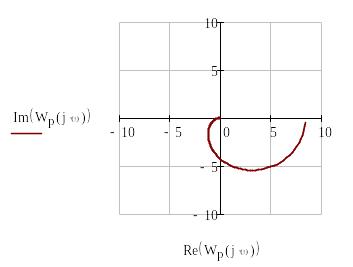
Для побудови амплітудно-фазно-частотної характеристики розімкненої системи (діаграми Найквіста) потрібно застосувати функції виділення дійсної частини комплексного числа Re та уявної частини – Im, як показано у прикладі, що поданий нижче.
До п. 2.
Визначити всі корені характеристичного рівняння у застосунку MathCAD можна найпростіше за допомогою засобів символьної (аналітичної) математики (для цього можна поставити курсор на змінну і вибрати пункт меню "Solve for Variable") або за допомогою вбудованої функції polyroots(<вектор-стовбець коефіцієнтів>).
Наприклад,
Задано характеристичне рівняння: A(s) := s4 + 1.3 s3 + 2.1 s2 + 1.2 s + 1.1 Вектор коефіцієнтів характеристичного рівняння, які впорядковані від меншого степеня до старшого: VA := [1.1 1.2 2.1 1.3 1] X := polyroots( VAT ) X = (виведення значення кореня) |
Універсальніший спосіб знаходження коренів чисельника та знаменника передатної функції САК (які називаються, відповідно, її нулями і полюсами) реалізується засобами символьної математики програми і дає змогу автоматизувати процес знаходження нулів/полюсів у випадку зміни як цілої передатної функції, так і її коефіцієнтів. Цей спосіб можна реалізувати двома шляхами, що показано далі як фрагмент документа MathCAD.
1) Знаходимо коефіцієнти поліномів чисельника і знаменника
Знаходимо нулі Z та полюси P передатної функції (корені поліномів чисельника та знаменника)
2) Інший спосіб знаходження нулів і полюсів лише засобами символьної математики
|
Для виведення графіка розміщення коренів характеристичного рівняння на комплексній площині за віссю X необхідно подати дійсну частину коренів (функція Re), за віссю Y – уявну (функція Im) (див. рис. 2.1). Масштаб осей координат – лінійний, для наочності бажано відобразити на графіку сітку (Grid lines).

Рис. 2.1. Приклад подання розміщення коренів характеристичного рівняння на комплексній площині
Для виведення на графік символів нулів ( ) та полюсів ( ) без з'єднуючих їх ліній потрібно у вікні форматування графіка (див. нижче) вибрати тип (Type) з'єднуючих ліній – точки (points) і відповідний тип символів у випадаючому меню.

До п. 3.
Для побудови перехідної характеристики
САК*)
з передатною функцією W(s), що
знаходиться за формулою
![]() ,
у застосунку MathCAD потрібно застосувати
зворотне перетворенням Лапласа (символьна
математика), а результат виводити з
трьома-чотирма десятковими цифрами
(цього досить для виведення графіка)
і результат присвоїти відповідній
перехідній функції.
,
у застосунку MathCAD потрібно застосувати
зворотне перетворенням Лапласа (символьна
математика), а результат виводити з
трьома-чотирма десятковими цифрами
(цього досить для виведення графіка)
і результат присвоїти відповідній
перехідній функції.
|
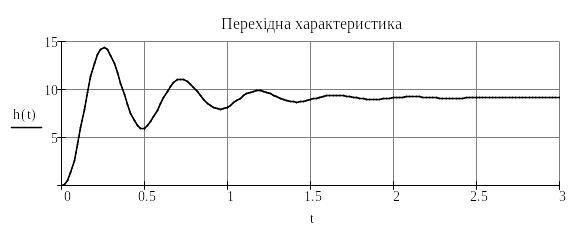
Часовий проміжок вибрати достатнім для відображення всієї перехідної характеристики на графіку до її майже повного загасання. |
Приклад знаходження перехідної характеристики в застосунку MathCAD із застосуванням зворотного перетворення Лапласа показано нижче.
Знаходимо перехідну характеристику системи
Задаємося часом відображення перехідної характеристики t : = 0, 0.01 . . 3
|