Методические указания
При решении задачи использовать метод сил. Для вычисления перемещений применять формулы сокращенного перемножения эпюр.
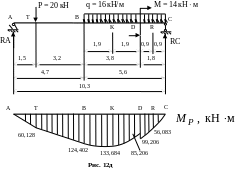
Пример 15: Для
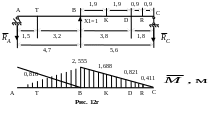
балки (рис. 12, а)
построить эпюры поперечных сил Q
и изгибающих моментов M;
выполнить статическую и кинематическую
проверку; подобрать двутавровое сечение.
Допускаемое напряжение
Решение:
1. Находим степень статической неопределимости (число опорных связей минус три) n = 4 – 3=1.
2. Выбираем основную систему в виде балки на двух шарнирных опорах (рис. 12, б).
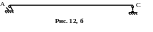
3. Показываем эквивалентную систему (рис. 12, в).
4. Составляем каноническое уравнение по методу сил:
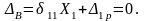
5.
Для определения перемещени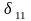й
и
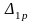предварительно построим эпюры изгибающих
моментов в основной системе при единичном
и грузовом состоянии. Перемещения будем
искать по формулам перемножения эпюр.
Для участков с распределённой нагрузкой
необходимо знать моменты на концах и в
серединах участков, для участков без
распределённой нагрузки достаточно
вычислить моменты на концах. Рассмотрим
единичное состояние (рис. 12, г).
Все размеры даны в метрах.
Определяем реакции опор:
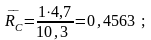
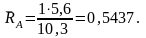
Проверка:
–0,5437+1
– 0,4563=1 – 1=0.
Реакции опор найдены верно.
Вычисляем
значения
в сечениях балки:
● точкаA:
●
точкаT:
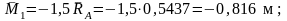
● точкаB:
●
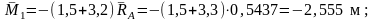
точкаK:
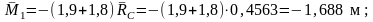
● точкаD:
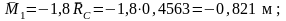
●точкаR: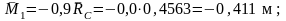
●точкаC: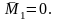
По найденным значениям строим эпюру (рис. 12, г).
Рассмотрим грузовое состояние основной системы (рис. 12д).
Определяем реакции опор:
;
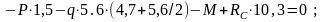
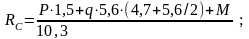
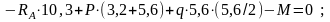
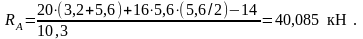
Проверка:
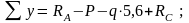
Реакции опор найдены верно.
Вычисляем значения моментов Mpв сечениях:
●точка
A:
●точка
T: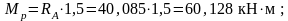
●точкаB:
●точка
K:
●слева от точкиD:
●справа
от точкиD:
●точкаR:
●точкаC:
По найденным значениям строим эпюру Mp(рис. 12, д).
Умножаем
эпюру
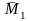саму на себя:
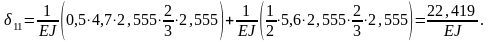
Перемножаем
эпюры
и Mp;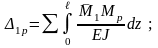
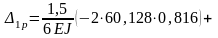
Из
уравнения
находим Х1 :
Строим
исправленную эпюру
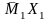(рис.
12, е).
Для этого все значения эпюры
(рис. 12, г)
умножаем на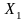
.
Строим
окончательную эпюру моментов M(рис.
12, е).
Для этого складываем эпюры
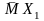и
.
Кинематическая
проверка:
+
.
Для построения эпюры поперечных сил Q используем эквивалентную систему и найденное значение . Определяем реакции опор в основной системе от действия заданной нагрузки и силы :
;
;
;
;
.
Проверка: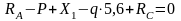
;
.
Реакции опор найдены верно.
Вычисляем поперечные силы Q.
●Участок AT:z1; 1,5;
Q(z1) = RA= 5,612 кН;
●Участок TB:z2; 3,2;
Q(z2) = RA–P= 5,612 – 20= –14,388 кН;
●Участок BD:z3; 3,8;
Q(z3) = RA–P+X1 – qz3= 5,612 – 20+63,406 – 16z3;
Q(z3) =49,018 – 16z3 ;
Q(0) =49,018 кН;Q(3,8) = –11,782 кН;
●Участок СD:z4; 1,8;
Q(z4) = –Rс +qz4= –40,582+16z4;Q(1,8) = –40,582+16·1,8= –11,782 кН;Q(0) = –40,582 кН.
По найденным значениям строим эпюру Q (рис.12, е).
Уточняем эпюру изгибающих моментов. Находим экстремальное значение изгибающего момента на участке BD:
Подбираем сечение балки из условия прочности по нормальным напряжениям; опасное поперечное сечение находится в точке D справа:
;
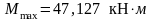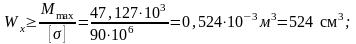
Принимаем двутавр № 33 (Wx=597 см3).