БДЗ № 1.

Системы счисления.

Система счисления – это код, в котором используют специальные символы для обозначения количества каких-либо объектов.

В повседневной жизни используется десятичная система счисления. В ней применяются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Общее количество символов в десятичной системе равно 10, поэтому ее называют системой счисления с основанием 10.

В разных областях компьютерной техники используются различные системы счисления. Например, при обработке временных диаграмм сигналов или поразрядной работе с ячейками памяти удобнее всего пользоваться двоичной системой счисления. Однако ее недостатком является большое количество 0 и 1, что может служить источником ошибок. Этим недостатком не обладают восьмеричная и шестнадцатеричная системы счисления, значения которых легко переводятся в двоичную систему счисления, и вместе с тем очень похожи на привычную для человека десятичную систему счисления.

Система счисления с основанием k должна иметь k символов для представления цифр от 0 до k-1:

• двоичная система 0, 1

• восьмеричная система 0, 1, 2, 3, 4, 5, 6, 7

• десятичная система 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

• шестнадцатеричная система 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F

Обобщенная запись числа по основанию b имеет вид:

(1.1)

где b – основание системы счисления, i – вес разряда, d – коэффициент.

Преобразование чисел.

Десятично-двоичное и обратное преобразование.

Для преобразования десятичного числа в двоичное находят наибольшее значение степени 2 , которое меньше данного числа и вычитают его из преобразуемого числа. Таким же образом поступают с остатком. Процесс продолжается до тех пор, пока данное число не окажется полностью разложенным на значения степеней 2. После этого его искомое двоичное представление можно скомпоновать из единиц, стоящих в битовых позициях, соответствующих имеющимся в полученном разложении степеням 2, и нулей в остальных позициях.

Пример 1.1. Преобразование десятичного числа 35.270 в двоичное представление.

	35.270 – 32 = 3.270
	3.270 – 2 = 1.270
	1.270 – 1 = 0.270
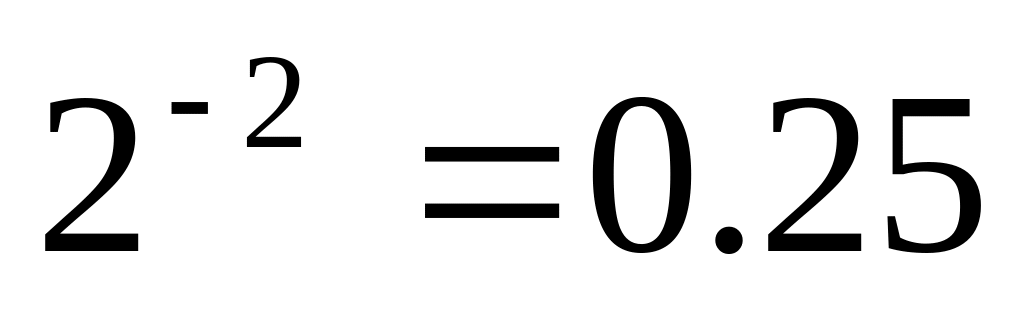
	0.270 – 0.25 = 0.02
	0.02 – 0.0156 = 0.0044
	0.0044 – 0.004

35.270 = 100011.01000101, т.е. в 5, 1, 0, -2, -6, -8 разрядах стоят единицы, в остальных разрядах – нули.

Преобразование двоичного числа в десятичное состоит в суммировании значений степени 2, соответствующих тем разрядам (битам) двоичного числа, где стоят единицы (согласно формуле 1.1).

Пример 1.2. Преобразование двоичного числа 100011.01000101 в десятичное представление.

100011.01000101 = + + + + + = 32 + 2 + 1 + 0.25 + 0.0156 + 0.004 = 35.2696

Десятично-двоичное преобразование целых чисел.

Рассмотрим преобразование чисел из десятичной системы счисления в двоичную и обратно.

Преобразуем десятичное число 12 в двоичное. Для этого разделим его на основание той системы счисления, в которую переводим число. В данном случае будем делить на 2. Воспользуемся обозначениями, принятыми в языке С++:

/ - деление (в том числе и целочисленное)

% - остаток от целочисленного деления

I шаг. 12 / 2 = 6 делим 12 на 2 нацело.

12 % 2 = 0 вычисляем остаток от деления и получаем число,

соответствующее разряду с весом 0.

II шаг. 6 / 2 = 3 делим результат целочисленного деления на 2.

6 % 2 = 0 вычисляем остаток от деления и получаем число,

соответствующее разряду с весом 1.

III шаг. 3 / 2 = 1 делим результат целочисленного деления на 2.

3 % 2 = 1 вычисляем остаток от деления и получаем число,

соответствующее разряду с весом 2.

IV шаг. 1 / 2 = 0 делим результат целочисленного деления на 2.

Получение нулевого значения служит

признаком завершения преобразования.

1 % 2 = 1 вычисляем остаток от целочисленного деления и получаем число, соответствующее разряду с весом 3

Расположив остатки от целочисленного деления в соответствии с весами их разрядов, получаем двоичное число: 1100.

Обратные преобразования производятся в соответствии с формулой (1.1):

1100 ₂ = 1  2³ + 1  2² + 0  2¹ + 0  2⁰ = 8 + 4 = 12₁₀

Пример 1.3. Преобразуем десятичное число 37 в двоичную систему счисления и обратно.

37/2=18 37%2=1 2

18/2=9 18%2=0 2

9/2=4 9%2=1 2

4/2=2 4%2=0 2

2/2=1 2%2=0 2

1/2=0 1%2=1 2

Получим 100101.

Проведем обратные, то есть двоично–десятичные преобразования, чтобы убедиться в том, что мы все сделали правильно при десятично-двоичных преобразованиях:

100101₂ = 1  2 + 0  2 + 0  2 + 1  2 + 0  2 + 1  2 = 37₁₀

Восьмеричная и шестнадцатеричная системы счисления

Многие ЭВМ используют восьмеричную или шестнадцатеричную форму записи, которые намного удобнее для человека и легко преобразуются в двоичную форму и обратно.

Восьмеричная запись, как и шестнадцатеричная, используется для более компактного и удобного представления двоичных чисел. Она содержит 8 цифр от 0 до 7 и является, таким образом, системой счисления с основанием 8.

Каждый шестнадцатеричный и каждый восьмеричный символ может быть представлен единственным сочетанием четырех бит, как это показано в таблице 1.1

Таблица 1.1

Десятичные	Шестнадцатеричные	Двоичные				Восьмеричные
		8	4	2	1
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15	0 1 2 3 4 5 6 7 8 9 A B C D E F	0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1	0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1	0 0 1 1 0 0 1 1 0 0 1 1 0 0 1 1	0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1	0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17

Для преобразования двоичного числа в шестнадцатеричное нужно начиная с младшего (крайнего правого) бита разбить двоичное число на группы по 4 бита (тетрады). Затем заменить каждую тетраду эквивалентной шестнадцатеричной цифрой. Если в старшей тетраде (крайней левой) не хватает элементов до четырех, нужно слева дополнить ее нулями. Обратное шестнадцатерично-двоичное преобразование также осуществляется с помощью таблицы.

Пример 1.4. Преобразование двоичного числа 00011101101110001110 в шестнадцатеричное представление (по таблице 1.1).

0001 1101 1011 1000 1110

1 D B 8 Е

Пример 1.5. Преобразование шестнадцатеричного числа 5DE8 в двоичное представление (по таблице 1.1).

5DE8 = 0101110111101000

Пример 1.6. Преобразуем двоичное число 11111010101 в его восьмеричное представление. Начиная с младшего бита двоичного числа, делим его на группы из трех бит (триады). Затем согласно таблице 1.1 преобразуем каждую триаду в эквивалентную восьмеричную цифру. При этом нули в старшем разряде двоичного числа, представленного в табл. 1.1 игнорируются.

Получим: 011 111 010 101 - двоичное

3 7 2 5 - восьмеричное

Если старшая триада оказывается частично заполненной, слева приписывают нужное количество нулей.

Пример 1.7. Преобразуем восьмеричное число 6530 в его двоичное представление: 6530 = 110101011000.

Следует обратить особое внимание, что нельзя производить перевод десятичных чисел в восьмеричные или в шестнадцатеричные и обратно с помощью таблицы 1.1!