20. Математические основы работы с графикой. Аффинные и полиномиальные преобразования

При работе с трехмерными объектами, часто требуется совершать по отношению к ним различные преобразования: двигать, поворачивать, сжимать, растягивать, скашивать и т.д. При этом в большинстве случаев требуется, чтобы после применения этих преобразований сохранялись определенные свойства.

Если растянуть вдоль какого-то направления круг, то получится лекальная кривая - эллипс. Если растянуть квадрат в направлении, параллельном одной паре сторон, то получится прямоугольник. Если же квадрат растянуть или сжать в направлении его диагонали, то получится параллелограмм. Но что такое растяжение и сжатие? Как их строго определить? Растяжения и сжатия, о которых мы будем говорить, в определенном смысле, равномерные. Эта равномерность означает, что все кусочки плоскости будут растягиваться (сжиматься) одинаково. Кроме того, когда мы растягиваем (сжимаем) квадрат, его стороны -- отрезки остаются отрезками. Такие равномерные растяжения (сжатия) называются аффинными преобразованиями.

Определение. Преобразование плоскости называется аффинным (от англ. affinity – родство), если

• оно взаимно однозначно;

• образом любой прямой является прямая.

Преобразование называется взаимно однозначным, если

• разные точки переходят в разные;

• в каждую точку переходит какая-то точка.

Частным случаем аффинных преобразований являются просто движения (без какого-либо сжатия или растяжения). Движения — это параллельные переносы, повороты, различные симметрии и их комбинации. Другой важный случай аффинных преобразований — это растяжения и сжатия относительно прямой.

Примеры движений

Примеры аффинных преобразований

Обозначим множество движений плоскости как , а множество аффинных преобразований как . Тогда верно следующее утверждение: Множество движений есть подмножество множества аффинных преобразований.

Это кажется очевидным. Давайте поймем, что нам собственно нужно доказать. Для этого нужно ещё раз посмотреть на определения движения и аффинных преобразований. Нужно доказать, что любое движение является аффинным. То есть нужно показать, что при движении разные точки переходят в разные, и образ любой прямой есть прямая.

Это интуитивно ясно — при движении фигуры вообще не меняют своей формы и размеров, а меняют лишь своё положение на плоскости. Также и прямые будут сохранять свою форму — оставаться прямыми. Движение можно представлять как перемещение листка бумаги с рисунком по парте. При движении разные точки остаются разными, поскольку расстояния сохраняются. Если точки были «разделены» некоторым расстоянием, то и после движения они будут «разделены» этим же расстоянием.

Свойства аффинного преобразования в трехмерном пространстве:

• отображает n-мерный объект в n-мерный: точку в точку, линию в линию, поверхность в поверхность;

• сохраняет параллельность линий и плоскостей;

• сохраняет пропорции параллельных объектов – длин отрезков на параллельных прямых и площадей на параллельных плоскостях.

Р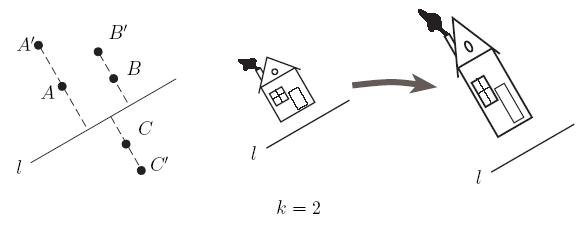 астяжение (сжатие) относительно прямой есть аффинное преобразования.

И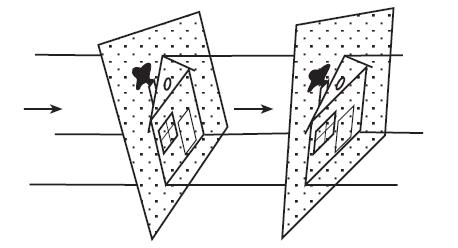 так, кроме движений плоскости аффинные преобразования содержат еще сжатия и растяжения относительно прямой. Если мы применим растяжение относительно одной прямой, а потом относительно другой прямой, то снова получим аффинное преобразование, так как и первое, и второе растяжение сохраняло прямые и разные точки переводило в разные.

Параллельное проектирование с одной плоскости на другую тоже аффинные преобразования

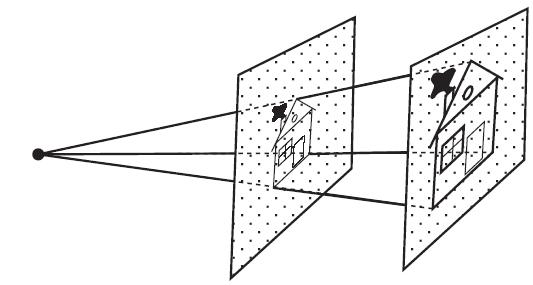
И проецирование тоже

Из определения аффинных преобразований видно, что они сохраняют прямые и свойство различия двух точек

Формулы полиноминальных преобразований используются для перевода исходных координат (обычно локальных-прямоугольных) в конечные (обычно спроектированные - прямоугольные). В зависимости от искажения изображения, количества контрольных точек (GCP – ground control point), и их размещения относительно друг друга, для выражения необходимого преобразования могут потребоваться достаточно сложные полиноминальные формулы. Сложность полинома выражается через его порядок. Порядок – это показатель наивысшей степени, используемой в полиноме.

Преобразование 1-го порядка – линейное преобразование. Это преобразование может изменять:

• положение по X и/или Y; Изменение положения, смещает изображение на определенное число пикселей по X и Y.

• масштаб по X и/или Y; Коэффициенты масштабирования по X и Y могут быть различными

• наклон по X и/или Y;

• поворот; При повороте, можно определить любое положительное или отрицательное число градусов, для поворота по- и против часовой стрелки соответственно. Поворот происходит вокруг центрального пикселя изображения.

• Отражение; слева направо, сверху вниз, сверху вниз и слева направо (аналогично повороту на 180 градусов)

П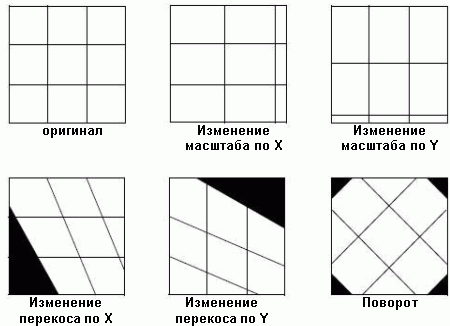 реобразование 1-го порядка может быть использовано для перевода исходного (например только что отсканированного) изображения в прямоугольную систему координат, преобразования одной прямоугольной системы координат в другую, обычно это преобразование используется для относительной небольших фрагментов.

Примерами применения этого преобразования могут быть: исправление перекосов в данных дистанционного зондирования, поворота отсканированных топографических листов, и поворота данных с нисходящих орбит так, что бы север был вверху изображения (а не по ходу орбиты).

Преобразование 1-го порядка также может быть использовано для данных, которые уже спроецированы на плоскость. Например, часто данные дистанционного зондирования, уже находятся в локальной прямоугольной системе координат, но не приведены к соответствующей проекции. При использовании данного типа преобразования, не имеет смысла увеличение порядка преобразования, если при первом порядке возникает большая среднеквадратическая ошибка. Сначала, необходимо проверить другие возможные источники ошибок: качество опорных точек, их распределение и другие возможные систематические ошибки. На рисунке показано, как изменяются данные при линейных преобразованиях. Для осуществления полиномиального преобразования первой степени необходимо найти 6 коэффициентов - по три на каждую координату (X и Y)

Н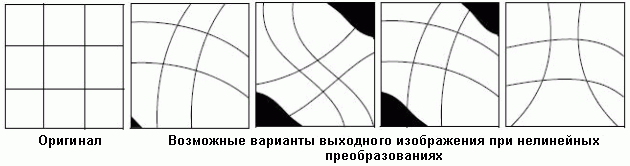 елинейные преобразования – это преобразования 2-го и более порядка. Эти преобразования могут корректировать нелинейные искажения. На рисунке изображены примеры результатов некоторых нелинейных преобразований.

Преобразования 2-го порядка могут быть использованы для преобразования данных в географической системе координат (широта, долгота) в прямоугольную, для преобразования данных больших областей (для учета кривизны Земли), для точно привязки искаженных по той или иной причине данных (например, из-за искажений линз камеры, плохо отсканированных материалов) и т.д.