Лекция 13.

Одношаговый метод Эйлера при решении задачи Коши.

Это простейший метод, позволяющий интегрировать ОДУ первого порядка. Его точность невелика, поэтому он крайне редко используется на практике, однако на основе этого метода легче понять алгоритмы других, более эффективных методов.

Метод Эйлера основан на разложении функции в ряд Тейлора в окрестности точки x₀

(3)

Необходимо отметить, что применение разложения функции в степенной ряд допустимо как к линейным ДУ, так и к очень широкому классу нелинейных ДУ произвольного порядка, что делает степенной ряд незаменимым при изучении очень большого числа самых разнообразных технических задач.

Графически представим решение в следующем виде.

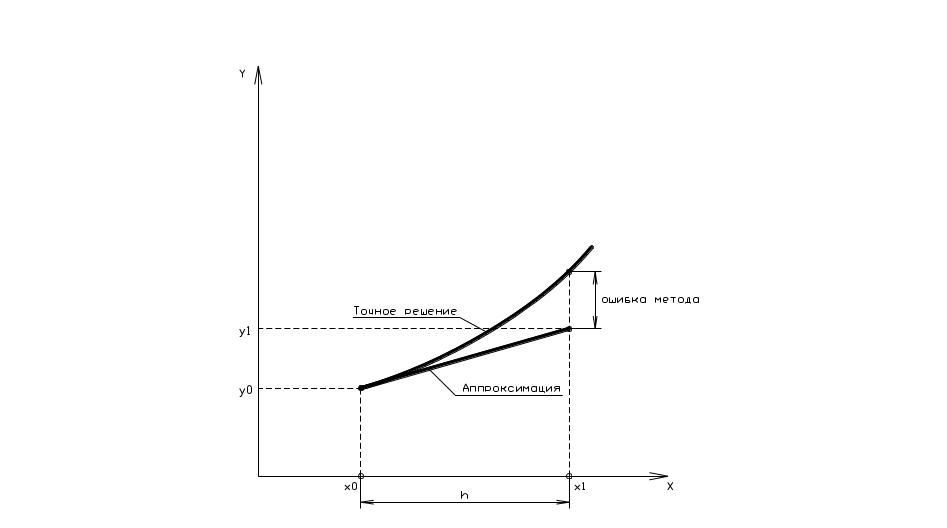
Рис. 1 – Графическое представление метода Эйлера

Очевидно, что если шаг h мал (меньше 1), то члены, содержащие h в более высоких степенях, являются малыми более высоких порядков, и ими можно пренебречь. Тогда

. (4)

Значение находят из правой части уравнения (1), подставив в него начальное условие (2), т.е. .

Таким образом, можно получить приближенное значение искомой функции y=y(x) при малом смещении h независимой переменной x от начальной точки x₀. Этот процесс можно продолжить, используя соотношение , где k = 0, 1, 2,… и делая сколь угодно много шагов. Подобные формулы, где результативные данные, полученные в очередном k-м шаге, возвращаются затем в виде исходных данных для вычисления значения в следующем k+1 шаге, получили название рекуррентных.

Ошибка метода Эйлера имеет порядок h², так как член h² и все последующие члены в более высоких степенях ряда (3), отбрасываются.

Модифицированный метод Эйлера.

Заметим, что если в точке x₀ имеем точное значение производной (равное тангенсу угла наклона), то с изменением независимой переменной x оно меняется, поэтому меняется и наклон касательной. Следовательно, при сохранении первоначально наклона касательной в результаты вычислений вносится погрешность на всем интервале h.

Точность метода Эйлера можно повысить, улучшив аппроксимацию производной. Например, если использовать вместо значения производной в начале интервала (в точке x₀) среднее арифметическое значение двух производных: в начале интервала и в конце (в точке x₀+h).

В модифицированном методе Эйлера сначала вычисляют значение функции в следующей точке по обычному методу Эйлера

, (5)

затем используют это значение для вычисления приближенного значения производной в конце интервала (как бы для следующего участка). Вычислив среднее между этим значением производной и значением в начале интервала, находят более точное значение y_k+1, а именно

. (6)

Принцип модифицированного метода Эйлера можно пояснить иначе. Рассмотрим ряд Тейлора (3). Чтобы сохранить член с h², надо знать вторую производную , которую можно в простейшем варианте аппроксимировать разностью

. (7)

Подставив выражение (7) в ряд Тейлора (3), получим

.

Погрешность модифицированного метода Эйлера имеет порядок h³. Соответственно, более высокая точность требует дополнительных вычислений. Для еще большего уточнения необходимо увеличивать число членов ряда Тейлора.

Методы Рунге-Кутты.

Чтобы удержать в ряде Тейлора член n-го порядка, необходимо каким-то способом вычислить n-ую производную. В модифицированном методе Эйлера для вычисления второй производной применена конечно-разностная схема, т.е. достаточно было знать наклоны кривой на концах рассматриваемого интервала. Для вычисления третьей производной в конечно-разностном виде необходимо знать дополнительно наклон в некоторой промежуточной точке интервала. Для вычисления четвертой производной нужно знать наклон в двух промежуточных точках.

Методы Рунге-Кутты дают набор формул для расчета координат внутренних точек. Наиболее распространенным является метод, согласно которому удерживаются члены с h⁴. Расчеты при использовании этого метода производят по формуле

,

где , , , .

Чтобы обеспечить высокую эффективность вычислительного процесса, величину h следует выбирать из соображений максимально допустимой ошибки на шаге. Такой выбор включается в алгоритм решения, где разница между предыдущим и последующим значением искомой функции не должна превышать некоторого заранее заданного значения.

Методы Рунге-Кутты для системы ОДУ.

Известно, что любое ДУ n-ого порядка можно свести к n ДУ первого порядка. Следовательно, для их решения можно использовать любую из формул Рунге-Кутты.

Например, в ОДУ второго порядка

(8)

можно принять обозначение , следовательно .

В результате этого выражение (8) можно представить в виде

, (9)

где формально введена функция .

Задача Коши для системы уравнений (9) содержит два начальных условия

Обобщенная характеристика одношаговых методов.

Всем одношаговым методам присущи определенные черты.

1. Для вычисления искомой функции в очередной точке необходимы данные лишь об одной предыдущей точке – свойство «самостарта». Это свойство позволяет легко менять шаг h.

2. В основе всех одношаговых методов лежит разложение функции в ряд Тейлора, в котором сохраняются члены, содержащие h в степени m. Число m является целым и называется порядком метода. Погрешность метода имеет порядок m+1.

3. Все одношаговые методы не требуют вычисления производной, вычисляют лишь саму функцию. Однако могут потребоваться ее значения в нескольких промежуточных точках.