Министерство образования Российской Федерации

Федеральное государственное образовательное учреждение

высшего профессионального образования

«Сибирский федеральный университет»

Институт цветных металлов и золота

С.В. Беляев, И.Н. Довженко, А.С. Пещанский,

Р.Е. Соколов, Э.А. Рудницкий

ТЕХНОЛОГИЧЕСКИЕ ПАРАМЕТРЫ

ПРОЦЕССА ПРЕССОВАНИЯ

Методические указания к практическим занятиям по курсу

«Технология прессования» для магистров по направлению 150100.68 Металлургия

Красноярск 2007

Содержание

содержание 2

ВВЕДЕНИЕ 3

1. Расчет сопротивления деформации сталей и сплавов 4

Вопросы для самоконтроля 17

Варианты заданий к разделу 1 17

2. РАСЧЕТ УСИЛИЯ ПРЕССОВАНИЯ 18

Вопросы для самоконтроля 23

Варианты заданий к разделу 2 23

3. РАСЧЕТ ТЕМПЕРАТУРНЫХ УСЛОВИЙ ПРОЦЕССА ПРЕССОВАНИЯ 26

Вопросы для самоконтроля 30

Варианты заданий к разделу 3 31

4. ОПТИМИЗАЦИЯ ТЕМПЕРАТУРНО-СКОРОСТНЫХ ПАРАМЕТРОВ ПРОЦЕССА ПРЕССОВАНИЯ ДЛЯ ДОСТИЖЕНИЯ МАКСИМАЛЬНОЙ ПРОИЗВОДИТЕЛЬНОСТИ И ТРЕБУЕМОГО УРОВНЯ КАЧЕСТВА ПРЕСС-ИЗДЕЛИЙ 32

Вопросы для самоконтроля 35

Варианты заданий к разделу 4 36

5. ПРОЕКТИРОВАНИЕ ПРЕСС-МАТРИЦ 36

Вопросы для самоконтроля 43

Варианты заданий к разделу 5 44

6. ОПРЕДЕЛЕНИЕ РАЗМЕРОВ ЗАГОТОВКИ ДЛЯ ПРЕССОВАНИЯ 44

Вопросы для самоконтроля 49

Варианты заданий к разделу 6 50

Библогафический список 51

Введение

Прутки, трубы и профили из сталей, цветных металлов и сплавов представляют собой высокоэффективный вид металлопродукции, широко применяемый в технике, строительстве и в быту. Основным способом их производства является прессование. Расчет технологических параметров процесса прессования позволяет оптимизировать данный процесс, достичь максимальной производительности и требуемого качества получаемой продукции.

1. Расчет сопротивления деформации сталей и сплавов

Определение силовых условий прессования необходимо для выбора оборудования, расчета инструмента, установления энергетических затрат и других показателей. Расчет усилия прессования позволяет прогнозировать возможность изготовления данного пресс-изделия, является в дальнейшем одним из основных технологических параметров для оптимизации существующей технологии.

Важнейшим показателем, необходимым для расчета силовых условий процессов прессования является сопротивление деформации σ_S, которое по С.И. Губкину является интенсивностью напряжений необходимых и достаточных для осуществления пластической деформации материала при заданных условиях деформирования. Вопрос определения реального значения σ_S для конкретного режима прессования по-прежнему является весьма актуальным, так как даже использование новых методов расчета с применением мощных ЭВМ незначительно повышают точность определения энергосиловых параметров процесса прессования, если важнейшую характеристику деформируемого металла – его σ_S – задают со значительными погрешностями.

Согласно теории максимальных касательных напряжений течение металла всегда начинается под действием нагрузки, равной наибольшему касательному напряжению. Если обозначить главные нормальные напряжения σ₁, σ₂, σ₃, то согласно этой теории:

(1)

или

(2)

Разность главных напряжений, необходимая для начала пластического течения, и является сопротивлением деформации σ_S. В соответствии с гипотезой максимальных касательных напряжений среднее главное напряжение σ₂ не оказывает влияния на начало пластической деформации. Однако, по исследованиям В. Лодэ, а также М. Роша и П. Айхингера, влияние σ₂ может все же иметь место. При этом течение материала начинается в том случае, когда работа упругого формоизменения превышает определенный предел. Условие пластичности записывается в этом случае в виде:

(3)

Наибольшие отклонения значений σ_S, определяемых по гипотезе формоизменения, от тех значений, которые определяются по гипотезе максимальных касательных напряжений, не превышают 15 %. Сопротивление деформации σ_S – это не константа материала, а переменная величина, зависящая от свойств материала и параметров процесса деформации.

При прессовании в отличие от большинства других методов обработки металлов давлением деформируемый материал находится под действием трех сжимающих главных напряжений. Наибольшее – осевое напряжение σ_1. Тангенциальное и радиальное напряжения σ₂ и σ₃ для цилиндрической заготовки являются равными величинами, сумма которых меньше величины осевого напряжения. Следовательно, можно записать:

(4)

Для частных случаев прессования характерно осесимметричное или плоское напряженно-деформированное состояние (что зависит от формы контейнера и прессуемого профиля), при котором сопротивление деформации будет равно разнице главных напряжений:

(5)

где β =1,0 ÷ 1,15 – коэффициент Лодэ.

Степень деформации при прессовании выражается натуральным логарифмом отношения площадей поперечного сечения распрессованной заготовки, которая равна площади контейнера F_К, и пресс-изделия F_ПР, т. е. коэффициента вытяжки:

(6)

и определяется как

(7)

Из общего определения скорости деформации можно записать:

(8)

где τ_D – длительность деформации соответственно.

Для процесса прессования характерна значительная неравномерность скоростей деформации в поперечном сечении деформационной зоны, поэтому чаще рассчитывают не истинные скорости и их распределение, а среднюю скорость деформации. Для расчета средних скоростей деформации профиля έ_{ср пр} и трубы έ_{ср тр} могут быть рекомендованы следующие формулы:

; (9)

, (10)

где v_пр – скорость движения пресс-шайбы; α_М – угол матрицы; D_ОП.ОКР, D_ТР и d_И – диаметр описанной окружности профиля, наружный и внутренний диаметры трубы соответственно.

Течение металла из контейнера происходит под действием силы гидравлического пресса Р_ОБ, создаваемой давлением жидкости р_ЖВД на главный плунжер пресса площадью F_ГП. Тогда максимальное усилие пресса будет равно:

(11)

Усилие, необходимое для выдавливания металла из контейнера через рабочий канал в матрице, называют усилием прессования. Для определения фактического усилия прессования Р_ПР по показанию манометра необходимо максимальное усилие пресса разделить на наибольшее давление жидкости р_ЖВД, на которое рассчитан пресс, и полученный результат умножить на показание манометра р_МАН в данный момент прессования:

(12)

Усилие прессования, отнесенное к площади сечения контейнера F_K, называют удельным усилием истечения или давлением прессования:

(13)

В общем виде давление прессования линейно зависит от сопротивления деформации σ_S:

(14)

где К_ПР – коэффициент, зависящий от способа прессования, параметров деформации, трения и т.д.

Сопротивление деформации σ_S при прессовании можно определить проведением натурных экспериментов, экспериментально и аналитически на основе математической обработки экспериментальных данных.

При определении σ_S путем натурных экспериментов при прессовании используют выражение (14) и получают наиболее точные результаты при корректном расчете коэффициента К_ПР. Однако такие эксперименты в условиях производства трудоемки, дорогостоящи и зачастую, особенно для новых разновидностей процесса, вообще невозможны.

При проведении лабораторных экспериментов необходимо использовать такой метод механического испытания материала, при котором обеспечивалось бы равенство соотношений напряжений и деформаций при испытаниях и технологическом процессе. Данное условие, как правило, невыполнимо. Поэтому результаты лабораторных исследований могут быть менее точными, а эксперимент также остается довольно трудоемким, хотя и менее дорогостоящим.

Аналитические методы определения σ_S менее точны, однако они не требуют больших затрат, а главное - позволяют установить влияние отдельных параметров процесса прессования на σ_S и дать их количественную оценку.

Единственно достоверным экспериментальным способом определения σ_S, при котором возможно достижение тех степеней деформации, соизмеримых с реализуемыми в процессах прессования, является метод испытания на горячее скручивание образцов разного диаметра, предложенный в работах Д.И. Суярова, Р. Мура, К. Вебера, Шварцбарта, В.П. Степанова. Сущность этого метода сводится к определению разности крутящих моментов при скручивании двух стандартных образцов с разными диаметрами в рабочей части, что сводит к минимуму ошибки, связанной с неравномерным распределением скорости и величины деформации в поперечном сечении сплошного образца.

В энергосиловых расчетах И.Л. Перлин применяет несколько значений σ_S: среднее сопротивление деформации по ОЧПЗ, сопротивление деформации в начале и на выходе из ОЧПЗ – σ_SH и σ_SK соответственно. При этом σ_SH приравнивается линейному напряжению текучести при статическом растяжении (табл. 1), а , где С_У – коэффициент скоростного упрочнения, зависящий от длительности деформации τ_Д (времени пребывания прессуемого металла в ОЧПЗ) и вытяжки  (табл. 2).

Таблица 1

Значения σ_SH цветных металлов и сплавов, МПа

Металл или сплав	Температура, 0С
	500	550	600	650	700	750	800	850	900	950
1	2	3	4	5	6	7	8	9	10	11
Медь	60	55	50	44	38	32	26	20	18	15
Л68	–	–	45	40	35	30	25	20	-	-
Л63	80	60	35	30	27	24	20	15	-	-
ЛС59-1	-	-	20	17	15	13	11	09	-	-
ЛН65-5	160	120	90	80	50	30	20	-	-	-
БрАЖМц10-3-1,5	-	-	120	70	50	30	15	12	8	-
БрАЖН10-4-4	-	-	160	120	80	50	25	20	15	-
БрБ-2	-	-	-	-	100	60	40	35	-	-
БрКМцЗ-1	-	-	120	100	75	50	35	20	15	-
БрКН1-3	-	-	200	150	120	80	50	25	12	-
БрОФ6,5-0,4	-	-	200	180	160	140	120	-	-	-
БрХ0,5	-	-	160	140	120	70	60	40	20	16
БрОФ4-0,25	-	-	150	130	110	90	70	-	-	-
Л96	80	70	65	58	50	42	35	26	-	-
Температура, 0С	750	800	850	900	950	1000	1050	1100	1150	1200
Никель	-	113	95	76	65	54	46	38	-	-
НМц5	-	160	140	110	90	60	50	40	30	25
НЖМц28-2,5-1,5	-	145	122	101	82	63	51	44	-	-
НМ19	104	81	59	43	28	17	-	-	-	-
МНЖМц3О-0,8-1,0	80	60	48	37	-	-	-	-	-	-
МНЖ5-1	75	50	35	25	20	15	-	-	-	-
Температура, 0С	200	250	300	350	400	450	500	-	-	-
Алюминий	50	35	25	20	15	-	-	-	-	-
АВ	55	40	30	25	22	12	-	-	-	-
АМг7	-	-	80	60	40	35	23	-	-	-
Д1	-	-	55	45	35	30	25	-	-	-
Д16	-	-	70	50	40	35	28	-	-	-
В95	-	-	100	80	65	50	35	-	-	-
АМг5	-	-	-	42	32	27	20	-	-	-
Магний	40	25	20	16	12	10	-	-	-	-
МА1	-	-	40	34	30	25	-	-	-	-
МА2 , МА8	-	-	70	55	40	28	-	-	-	-
МАЗ	-	-	60	50	35	28	-	-	-	-
МА5	-	-	52	45	40	35	-	-	-	-
продолжение таблицы 1
Температура, 0С	600	700	800	850	900	950	1000	1100	-	-
ВТ1	260	120	50	40	30	25	20	-	-	-
ВТ5	430	250	160	135	110	70	36	17	-	-
Температура, 0С	100	150	200	250	300	350	400	-	-	-
Цинк	78	3,6	24	14	12	1,0	-	-	-	-

Таблица 2

Значения скоростного коэффициента С_У

Вытяжка λ	Длительность деформации τД, сек.
	0,001	0,01	0,1	1,0	10
5	4,7	4,4	3,4	2,6	1,0
>10	5,0	4,8	3,6	2,8	1,0

Л.А. Шофман берет значения сопротивления деформации с учетом влияния на сопротивление деформации температурно-скоростных условий процесса прессования. Это учитывается при помощи дополнительных коэффициентов:

(15)

Температурный коэффициент ω_Т определяется из выражения:

(16)

где Т_ПЛ и Т_ПР – абсолютные температуры плавления и прессования, °К;

Скоростной коэффициент φ_V определяется из выражения:

(17)

где έ_ср - средняя скорость деформации в процессе установившегося истечения и рассчитывается по формулам:

- для прутков

; (18)

- для труб

. (19)

При прессовании труб, прутков методами прямого и обратного истечения b_пр коэффициент соответственно равен 0,7; 0,8; 0,3.

Коэффициент n определяется из выражения:

(20)

где n₀= 0,18÷0,20 для алюминия и его сплавов; n₀ = 0,20÷0,25 для меди и ее сплавов.

Значения σ_S0 для различных металлов так же, как у И.Л. Перлина, приравниваются линейному напряжению текучести при статическом растяжении: медь – 18÷20 МПа; алюминий – 16÷17 МПа; АМц – 25 МПа; Д1 – 35 МПа; Д16 – 38 МПа.

Следует отметить, что при проведении механических испытаний на растяжение невозможно достигнуть таких степеней деформации, которые соответствуют степеням деформации, реализуемых в производственных условиях, а при кручении – очень сложно обеспечить скорости деформации, особенно для скоростных процессов прессования таких материалов, как сталь. Поэтому необходимо проводить пересчет скоростей деформации с использованием эмпирических коэффициентов (табл. 3).

Таблица 3

Коэффициенты пересчета скоростей деформации

Тип стали	Скорость деформации έ, с-1
	10-3	10-2	10-1	1	10	102	103
Углеродистые и низколегированные	0,74	0,90	1,00	1,20	1,04	0,85	-
Аустенитные	0,62	0,86	1,00	1,08	1,05	0,99	0,93

От известных методов нахождения σ_S выгодно отличается метод Н.Н. Довженко определения σ_SH во время прямого прессования без смазки заготовок различной длины. Во время прессования данных заготовок определяют максимальные усилия прессования, тогда сопротивление деформации будет равно:

(21)

где Р_ПР1 и Р_ПР2 – максимальные усилия прессования заготовок длиной L₁ и L₂ соответственно, причем L₁ > L₂; ∆L = L₁ – L₂; D_K – диаметр контейнера; π = 3,14; μ – коэффициент трения прессуемого металла о стенки контейнера.

Данный метод лишен тех недостатков, которые указаны выше для известных методов определения σ_S. Кроме того, возможно применение данного метода непосредственно в производственных условиях. Для этого в начале установившейся стадии необходимо найти изменение усилия прессования ∆Р_ПР в зависимости от перемещения пресс-штемпеля ∆L. Тогда текущее сопротивление деформации для прессуемого металла будет равно:

(22)

Данный метод позволяет оперативно находить σ_S во время прессования, корректировать процесс прессования для достижения оптимальных условий производства с использованием АСУП.

В зависимости от температуры деформация бывает холодной и горячей. Во время деформация в деформируемом металле происходят два противоположных процесса: упрочнение и разупрочнение. От соотношения скоростей протекания данных процессов зависит характер деформации.

При холодной деформации скорость упрочнения значительно больше скорости разупрочнения, а температура не превышает 0,3Т_ПЛ (Т_ПЛ – температура плавления в кельвинах, °К). С увеличением степени деформации растут показатели прочности, а пластичность снижается. Совокупность данных явлений, связанных с изменением свойств металла в процессе холодной пластической деформации, называется наклепом (рис. 1).

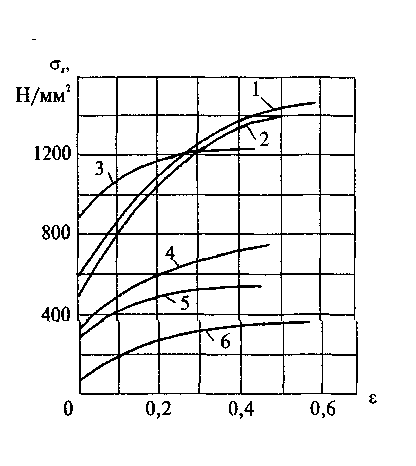
1 – сталь ЭИ69; 2 – сталь Х19Н9Т; 3 – сталь 40ХМА; 4 – латунь Л59; 5 – дюралюминий Д1; 6 – медь

Рис. 1. Кривые наклепа металлов и сплавов

При холодной деформации изменения структуры, механических свойств сильнее зависят от степени деформации ε и слабее от температуры и скорости деформации. Влияние степени деформации на изменение механических свойств при холодной деформации разных металлов наиболее полно представлено в работах А.В. Третьякова в виде следующих эмпирических формул:

- для σ_0,2, σ_В и НВ

(23)

- для δ

(24)

где y – текущее значение механической характеристики; y₀ – постоянная величина, равная исходному значению данной механической характеристики при нулевой степени деформации; x – текущее значение величины степени деформации ε; a, b, c – постоянные коэффициенты.

Применив уравнения (23), (24) к двум или трем каким-либо известным по механическим характеристикам и степени деформации экспериментальным точкам, можно определить постоянные коэффициенты и получить соответствующую эмпирическую зависимость.

В табл.4 приведены эмпирические формулы для определения значений временного сопротивления разрыву некоторых цветных металлов и сплавов.

Таблица 4

Предел прочности цветных металлов и сплавов при холодной деформации

№ п/п	Цветной металл или сплав	Марка	Формула
1	Алюминиевый	АД1, Д1, АМг3, АМг5	σВ = σВ0 +1,6ε 0,76
2	Титановый	ВТ1-1, ВТ1-2, ВТ4, ВТ6	σВ = σВ0 +2,4ε 0,63
3	Медь	М1, М2	σВ =σВ0+0,68ε 0,77
4	Бронзы	БрАЖН10-4-4, БрАЖМц10-3-1,5	σВ = σВ0 +2,9ε 0,70
5	Латуни	Л80, Л75, Л68, Л62, Л59, ЛС59-1	σВ =σВ0+0,77ε 0,91
6	Никелевые	МНМц3-12, НМц5, НМц2,5	σВ = σВ0 +1,3ε 0,83
7	Никелевые	МН5, ТПМН0,6, МН19	σВ = σВ0 +0,8ε 0,72

При температурах выше 0,4Т_ПЛ на процессы упрочнения накладывается мощный разупрочняющий процесс – рекристаллизация, которая характеризуется появлением новых зародышей и ростом новых равноосных зерен за счет энергии старых деформированных зерен. Если скорость упрочнения меньше скорости разупрочнения, то данную деформацию считают горячей, и она происходит при температурах больше (0,7÷0,9)Т_ПЛ.

Во время горячей деформации значительно снижается сопротивление деформации, повышается пластичность металла (рис. 2).

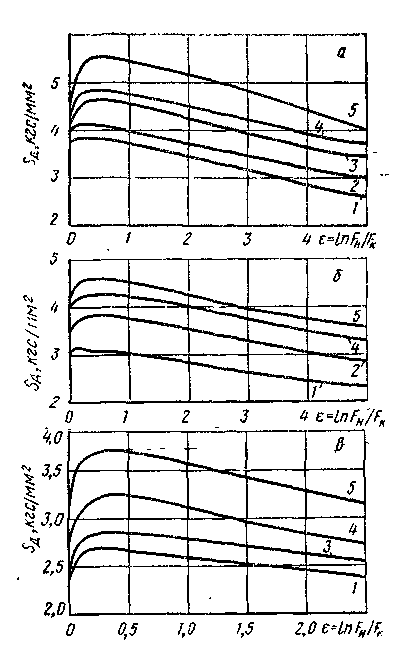
а – 450 °С; б – 500 °С; в – 550 °С; 1 – έ = 0,74 с-1; 2 – 1,48 с-1; 3 – 2,96 с-1; 4 – 7,4 с-1; 5 – 10,3 с-1

Рис. 2. Зависимость σ_S сплава АВ от параметров деформации, полученные метод кручения

На основе анализа многочисленных опытных данных экспериментального определения сопротивления деформации от основных параметров деформирования А.И. Целиковым была предложена следующая зависимость:

, (25)

где – термомеханические коэффициенты, зависящие от свойств деформируемого материала.

На основе математической обработки экспериментальных данных исследования сопротивления деформации различными авторами были получены следующие формулы для расчета сопротивления деформации:

- М. Жидеком:

; (26)

- В.Н. Выдриным, А.В. Третьяковым, В.И. Зюзиным:

; (27)

- М. Хайдуком:

, (28)

где А, В, С, В, D, K – реологические коэффициенты; Т – температура прессования; .

Анализ уравнений (25) – (28) показывает, что эта зависимость может быть описана: полиномом (26); степенной или экспоненциальной функцией (25, 27, 28) и не позволяет учитывать изменения значений σ_S в области фазовых превращений, при динамических процессах разупрочнения, при выделении избыточной фазы и являются правомерными лишь для однофазных областей. Поэтому при использовании формул (25) – (28) следует учитывать химический состав материала, степень деформации, скорость деформации и температуру. При отсутствии хотя бы одного из этих параметров область применения уравнения сразу ограничивается узким интервалом варьирования условий деформации. Для математического представления функциональной зависимости сопротивления деформации материала от условий деформации наиболее пригодными следует признать степенные и экспоненциальные функции (25, 27, 28), которые дают удовлетворительное приближение расчетных данных к экспериментальным значениям и являются достаточно простыми для практического применения. В табл. 5 представлены реологические коэффициенты для формулы (27).

Таблица 5

Значения реологических коэффициентов для формулы (27)

Материал	Температура, °С	Эмпирические коэффициенты
	Т	А	В	С	D
1	2	3	4	5	6
Чистые металлы
Железо	800-1200	1200	0,4	0,14	0,003
Никель	900-1300	1850	0,5	0,11	0,0028
Продолжение таблицы 5
Медь	450-1000	520	0,4	0,11	0,0023
Титан	200-750	1900	0,35	0,1	0,003
Алюминий	300-500	180	0,37	0,14	0,0017
Цинк литой	150-340	260	0,5	0,2	0,0057
Цинк прокат	20-100	420	0,15	0,13	0,0012
Ванадий	800-1200	2500	0,4	0,12	0,003
Цирконий	800-1100	3000	0,2	0,12	0,003
Ниобий	950-1200	2500	0,3	0,15	0,003
Молибден	950-1250	2900	0,25	0,15	0,003
Вольфрам	1600-2200	10000	0,3	0,12	0,0018
Свинец	20-300	46	0,35	0,12	0,0015
Сплавы алюминия
АМЦ	300-500	250	0,32	0,10	0,001
АМГ 61	300-450	410	0,35	0,15	0,0012
АМГ 6	300-450	440	0,35	0,11	0,0012
Д 16	300-450	370	0,32	0,11	0,0017
АМГ 58	300-450	350	0,35	0,13	0,0013
Сплавы меди
Л 62	300-600	1000	0,5	0,11	0,004
Л 68	600-750	700	0,5	0,11	0,007
Л 70	750-950	850	0,5	0,11	0,004
Л 90	300-600	710	0,38	0,11	0,0028
Мельхиор	600-900	620	0,57	0,11	0,0028
Монель - металл	450-900	1220	0,57	0,11	0,0035
Нейзильберг	450-900	750	0,4	0,11	0,003
Углеродистые и низколегированные стали
Сталь 10	900-1300	1200	0,25	0,15	0,0025
Сталь20	900-1300	1300	0,25	0,14	0,0025
Сталь 45	900-1300	1330	0,25	0,14	0,0025
Сталь 60	900-1300	1300	0,25	0,14	0,0025
Сталь 0	900-1300	1100	0,25	0,14	0,0025
Сталь 3	900-1300	1250	0,25	0,14	0,0025
Сталь 6	900-1200	1400	0,25	0,14	0,0025
У 8 и У 9	900-1200	1400	0,25	0,14	0,0027
У 12	900-1200	1700	0,25	0,15	0,0025
15ХСАД	300-1300	1450	0,25	0,14	0,003
40Х	900-1200	1400	0,25	0,14	0,003
40ХН	900-1300	1400	0,25	0,14	0,003
60Г	900-1200	1400	0,25	0,5	0,0027
12ХН3А	900-1300	2300	0,25	0,14	0,003
6ХС2, 55С	900-1300	1750	0,25	0,14	0,003
18 ХНВА	900-1200	2300	0,25	0,2	0,003
ХВГ	900-1300	1850	0,25	0,1	0,0027
30ХГСАН	900-1200	1600	0,25	0,1	0,003
Окончание таблиц 5
Высоколегированные стали и жаропрочные сплавы
1Х1	900-1300	4600	0,28	0,09	0,003
4Х13	900-1300	4300	0,28	0,09	0,003
Х17Н2	900-1300	7000	0,28	0,09	0,0037
Х18Н9Т	900-1300	3250	0,28	0,09	0,0028
Х110Н10Т	900-1300	3400	0,28	0,09	0,0028
Х18н12М2Т	900-1300	3800	0,28	0,09	0,0033

Следует отметить, что в формуле (27) разница в значениях реологических коэффициентах В, С и D для различных марок стали, цветных металлов и сплавов невелика, а значения коэффициента А изменяются в широких пределах: от 46 до 10000 МПа, т.е. в значительной степени точность расчетов будет зависеть от достоверности значений данного коэффициента.

Несмотря на наличие теоретических формул по влиянию степени и скорости деформации на сопротивление деформации, практически значение сопротивления деформации находят на основе соответствующих экспериментов.

В интервале степени деформации 10÷50 % при горячей деформации А.И. Целиков предлагает величину σ_S определять методом термомеханических коэффициентов, применив уравнения (25) к двум известным по механическим характеристикам и параметрам деформации экспериментальным значениям σ_S:

, (29)

где σ_S (ε₁, έ₁, Т₁) и σ_S (ε₁, έ₂, Т₂) – сопротивление деформации при постоянной деформации ε и различных скоростях έ₁и έ₂ и температурах Т₁ и Т₂.

В работе Я.М. Охрименко получены реологические уравнения _s для наиболее распространенных алюминиевых сплавов, используемых в прессовом производстве:

- для АД31

(30)

- для АК6

(31)

- для Д16

(32)

-для Амг6

(33)

где _s – МПа, t – ^оС.

Использование данных формул в расчетах дает погрешность не более 5 %, что является вполне приемлемым для инженерных расчетов.

Таким образом, существующие зависимости сопротивления деформации материала от условий деформирования позволяют найти σ_S в первом приближении, а для конкретного случая необходимо учитывать физико-химические свойства материала непосредственно во время деформирования и проводить корректировку реологических коэффициентов.