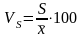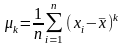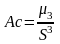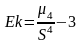Показатели вариации

Далее переходим к нахождении показателей вариации, которые характеризуют величину разброса наблюдаемых значений х1,х2,…,хn относительно среднего значения.

1. Дисперсия (мера рассеивания, отклонения случайных значений от среднего).

Исходные несгруппированные данные xi (100 набл.)		Интервальный вариационный ряд (xi - середина интервалов)
По формуле	С помощью функции Excel
	ДИСПР( )
0.08866675	0.08866675	0.093041062

2. Среднее квадратическое отклонение (описывает абсолютный разброс значений показателя X, находится как квадратный корень из дисперсии, чтобы показывать разброс в тех же единицах измерения, что и сама величина Х и ее средние значения).

Исходные несгруппированные данные xi (100 набл.)		Интервальный вариационный ряд (xi - середина интервалов)
По формуле	С помощью функции Excel
	-
0.297769626	-	0.30502633

3. Коэффициент вариации (мера относительного разброса случайной величины).

Исходные несгруппированные данные xi (100 набл.)		Интервальный вариационный ряд (xi - середина интервалов)
По формуле	С помощью функции Excel
	-
46.7089609 %	-	47.80565483 %

Полученный нами коэффициент вариации существенно меньше 100%, что говорит о том, что исследуемые данные однородны.

12. Центральный момент k-го порядка (среднее значение k-й степени отклонения индивидуальных значений признака от его среднеарифметической величины).

Исходные несгруппированные данные xi (100 набл.)		Интервальный вариационный ряд (xi - середина интервалов)
По формуле	С помощью функции Excel
	-

На практике используются центральные моменты порядка 1,2,3 и 4 порядка.

4. Центральный момент 1 порядка (он всегда равен нулю согласно формулам расчета):

Исходные несгруппированные данные xi (100 набл.)		Интервальный вариационный ряд (xi - середина интервалов)
По формуле	С помощью функции Excel
-6.4948E-17	-	0

Полученные значения совсем немного отличаются от нуля вследствие промежуточных округления в ячейках при вычислениях в Excel.

5. Центральный момент 2 порядка (это – дисперсия величины Х):

Исходные несгруппированные данные xi (100 набл.)		Интервальный вариационный ряд (xi - середина интервалов)
По формуле	С помощью функции Excel
0.08866675	-	0.093041062

6. Центральный момент 3 порядка (на его основе можно построить показатель, характеризующий степень асимметричности распределения – коэффициент асимметрии):

Исходные несгруппированные данные xi (100 набл.)		Интервальный вариационный ряд (xi - середина интервалов)
По формуле	С помощью функции Excel
0.014486666	-	0.014960136

7. Центральный момент 4 порядка (с его помощью характеризуется островершинность/плосковершинность графиков рядов распределения, , называемая эксцессом):

Исходные несгруппированные данные xi (100 набл.)		Интервальный вариационный ряд (xi - середина интервалов)
По формуле	С помощью функции Excel
0.023948335	-	0.024449331

Центральные моменты 3-го и 4-го порядка используем для расчета следующих двух коэффициентов.

8. Коэффициент асимметрии (числовая характеризующая степени несимметричности распределения данной случайной величины).

Исходные несгруппированные данные xi (100 набл.)		Интервальный вариационный ряд (xi - середина интервалов)
По формуле	С помощью функции Excel
	СКОС( )
0.548690284	0.55708157	0.527137057

В данном случае Ac>0, следовательно, имеет место правосторонняя асимметрия.

Коэффициент эксцесса (мера остроты пика графика распределения случайной величины).

Исходные несгруппированные данные xi (100 набл.)		Интервальный вариационный ряд (xi - середина интервалов)
По формуле	С помощью функции Excel
	ЭКСЦЕСС( )
0.046167239	0.111048414	-0.17565555

В данном случае эксцесс отрицательный (по ранж.дан.), это говорит о том, что график распределения имеет немного более плоскую вершину, чем нормальное распределение, но плосковершинность несущественна, т.к. коэффициент не превышает по модулю 0,5 и близок к нулю.

* По значениям показателей асимметрии и эксцесса распределения можно судить о близости распределения к нормальному, у которого эти коэффициенты равны нулю, что бывает существенно важно для практических исследований.

Сведем все полученные результаты в итоговую таблицу.

Таблица 3

Основные числовые характеристики распределения темпов роста курса акций 100 фирм.

Характеристика	Исходные несгруппированные данные		По интервальному ряду
	По формуле	Excel
Характеристики центра группирования
1. Ср. Арифмитичская	0.6375	0.6375	0.638054914
2. Ср. гармоническая	0.439403055	0.439403055	0.449699555
3. Ср. геометрическая	0.556418349	0.556418349	0.555262953
4. Медиана	0.615	0.615	0.602860873
5. Мода	0.72	0.72	0.501840943
Показатели вариации
6. Дисперсия	0.08866675	0.08866675	0.093041062
7. Ср. квадр. отклонение	0.297769626	-	0.30502633
8. Коэффициент вариации	46.7089609	-	47.80565483
9. Центр.момент 1-го порядка	-6.4948E-17	-	0
10. Центр.момент 2-го порядка	0.08866675	-	0.093041062
11. Центр.момент 3-го порядка	0.014486666	-	0.014960136
12. Центр.момент 4-го порядка	0.023948335	-	0.024449331
13. Коэф-т асимметрии	0.548690284	0.55708157	0.527137057
14. Коэф-т эксцеса	0.046167239	0.111048414	-0.17565555