Национальный исследовательский университет

«Высшая школа экономики»

Факультет экономики

Отделение статистики, анализа данных и демографии

Отчёт о проделанной работе

по курсу «Статистические и демографические методы анализа данных»

за 3 модуль

на тему «Статистические методы анализа одномерных данных»

Вариант 20

Выполнила: студентка гр. 11С

Морозова Алиса Сергеевна

Проверила: доцент каф.

Статистических методов к.т.н.

Миронкина Юлия Николаевна

Москва

Цель работы:

1. Построить интервальный вариационный ряд распределения признака.

2. Вычислить характеристики по исходным данным и интервальному вариационному ряду:

• Характеристики центра положения:

  • Средние значения: арифметическое, гармоническое и геометрическое;

  • Медиану;

  • Моду;

• Характеристика вариации (разброса данных)

• Дисперсию;

• Среднее квадратическое отклонение;

• Коэффициент вариации;

• Центральные моменты первого, второго, четвертого порядков;

• Коэффициент асимметрии;

• Коэффициент эксцесса.

3. Построить графики частот и относительных частот по интервальному вариационному ряду - гистограммы, полигона и кумуляты, а также исходных неранжированных и ранжированных данных в виде столбиковой диаграммы и точечного графика.

4. Проанализировать полученные данные и сделать выводы.

Исходные данные для анализа. По результатам выборочного обследования 100 однотипных предприятий получены данные темпа роста курса акций (табл.1)

Таблица 1

Темп роста курса акций 100 фирм по сравнению с предыдущим периодом (%)

0,38	0,77	0,53	1,01	0,36	0,65	1,26	0,91	0,50	0,05
0,45	0,39	0,41	0,42	0,55	0,71	1,42	0,38	0,65	0,80
0,46	0,24	1,11	0,60	0,37	0,68	1,29	0,32	0,72	0,53
1,05	1,10	0,25	0,91	0,72	0,68	1,10	0,50	0,77	0,48
0,68	0,52	0,33	0,15	0,51	1,20	0,44	0,78	0,93	0,26
0,70	0,48	0,24	0,48	0,66	1,32	0,57	0,71	0,26	0,77
0,51	0,72	1,10	0,72	1,40	0,63	0,86	0,58	0,07	0,57
0,76	0,77	0,52	0,35	1,25	0,79	0,89	0,71	0,27	0,82
0,82	0,35	0,48	0,55	0,33	0,28	0,66	0,82	0,09	0,44
0,36	0,68	0,72	0,60	0,34	0,42	0,70	0,97	0,79	0,59

1. Построение интервального вариационного ряда распределения.

Для упрощения анализа сначала необходимо было представить исходные данные в ранжированный ряд 100 наблюдений x_i в порядке возрастания значений. Однако просто ранжированные данные не представляют большой ценности для проведения расчетов, поэтому дальше возникает необходимость сгруппировать их - представить их в виде интервального вариационного ряда.

При построении интервального вариационного ряда необходимо выбрать оптимальное число групп (интервалов признака) и установить длину интервала. Для этого определим:

1. Минимальное x _min и максимальное x _max значения исходных данных.

Удобно использовать в этих целях функции МИН и МАКС в Excel.

xmin	0.05
xmax	1.42

2. Размах вариационного ряда: R=x_max-x_min

R

1.37

3. Оптимальную ширину интервала (шага h) по формуле Стерджеса:

где n – количество наблюдений (n=100 в нашем исследовании).

Используем функцию Excel LOG(100;2)/

h

0.179229

4. Границы интервального ряда:

a_i – нижние границы, b_i – верхние границы:

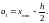
Если оказывается, что a₁<0, хотя по смыслу величина Х не может принимать отрицательные значения, то принимаем a₁=0.

Верхняя граница первого интервала b₁= a₁+h.

Тогда, если b_i - верхняя граница i-го интервала (причем a_i+1=b_i), то b₂=a₂+h, b₃=a₃+h и т.д.

Построение интервалов продолжается до тех пор, пока верхняя граница интервала не будет равной или больше x_max.

b₉= 1.433831266 ≥ x_max= 1.42

Таким образом, у нас получилось 8 интервалов.

Границы интервалов
ai (нижн)	bi (верхн)
0	0.179228908
0.179228908	0.358457817
0.358457817	0.537686725
0.537686725	0.716915633
0.716915633	0.896144541
0.896144541	1.07537345
1.07537345	1.254602358
1.254602358	1.433831266

5. Середины интервалов 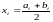, так как в интервальном ряду в качестве представителя каждого интервала используется его середина.

Середина интервала xi
0.089614454
0.268843362
0.448072271
0.627301179
0.806530087
0.985758996
1.164987904
1.344216812

6. Частоты встречаемости признака m_i в каждом интервале (подсчитаем вручную и с помощью функции Excel ЧАСТОТА) и накопленные частоты встречаемости m_i^н, суммируя все частоты, накопленные к текущему интервалу на каждом шаге.

Частота встречаемости mi			Накопленная частота mih
вручную	по формуле
	0
4	4	4
13	13	17
25	25	42
22	22	64
19	19	83
6	6	89
6	6	95
5	5	100

7. Относительные частоты w_i=m_i /n, показывающие доли всех наблюдений, попадающие в каждый интервал, и относительные накопленные частоты w_iн=m_{i н}/n.

Относительная частота wi	Относительная накопленная частота wih
0.04	0.04
0.13	0.17
0.25	0.42
0.22	0.64
0.19	0.83
0.06	0.89
0.06	0.95
0.05	1

Сведем все полученные результаты по построению интервального ряда в итоговую таблицу (табл. 2).

Таблица 2.

Интервальный вариационный ряд распределения темпов роста курса акций 100 фирм по сравнению с предыдущим периодом.

Границы интервалов		Середина интервала xi	Частота встречаемости mi		Накопленная частота mih		Относительная частота wi=mi /n		Относит. накопленная частота wiн=miн/n
ai (нижн)	bi (верхн)		вручную	по формуле
				0
0	0.179228908	0.089614454	4	4		4		0.04		0.04
0.179228908	0.358457817	0.268843362	13	13		17		0.13		0.17
0.358457817	0.537686725	0.448072271	25	25		42		0.25		0.42
0.537686725	0.716915633	0.627301179	22	22		64		0.22		0.64
0.716915633	0.896144541	0.806530087	19	19		83		0.19		0.83
0.896144541	1.07537345	0.985758996	6	6		89		0.6		0.89
1.07537345	1.254602358	1.164987904	6	6		95		0.6		0.95
1.254602358	1.433831266	1.344216812	5	5		100		0.5		1
			n=∑ mi=100				∑ wi =1