Повторение испытаний. Формула Бернулли.

На практике встречаются ситуации, когда многократно проводятся испытания в одних и тех же условиях. Если при этом вероятность появления события постоянна (не зависит от результатов предыдущих опытов), то повторение испытаний называется схемой Бернулли.

Пример 1.15. Стрелок производит три выстрела, вероятность попадания при каждом известна и равна р. Найти вероятность того, что мишень будет поражена один раз.

n=3 m=1 p	Событие Аi – попадание при i–ом выстреле ( ), событие В – мишень поражена один раз при трех выстрелах. , несовместные

Пусть произведено n испытаний, в каждом из которых событие наступает с вероятностью р, и не наступает с . Выведем формулу для вычисления вероятности того, что событие наступит m раз, т.е. P_n(m)=? .

Рассмотрим один вариант, когда событие наступит первые m раз.

Вероятность этого события равна .

Таких вариантов будет столько, сколько сочетаний выбора m чисел из n.

, Тогда - формула Бернулли.

Иногда данную формулу называют формулой биномиального распределения: .

Пример 1.16. Вероятность потери одного вызова на АТС 0,1. Найти вероятность того, что из пяти вызовов три закончатся разговором (не менее четырех закончатся разговором).0

	событие А – вызов окончится разговором. Тогда , а . , .
0

Локальная теорема Лапласа

В случаях, когда велико формула Бернулли становится непригодной, и используют приближенные формулы.

Теорема Если в каждом испытании вероятность наступления события постоянна и и , то вероятность наступления события раз в испытаниях приближенно определяется по формуле

,

где , - табулированная функция, значения которой приведены в пособиях по ТВ, - четная функция.

Замечание Эта формула является асимптотической, т. е. точность вычисления тем выше, чем больше . Она дает большую погрешность (не пригодна) при малых значениях . Общепринято при использовать формулу Пуассона.

Формула Пуассона

Пусть так что ,

.

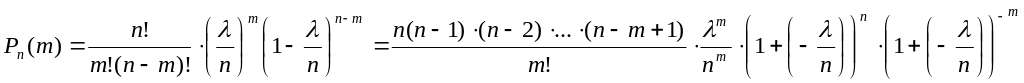
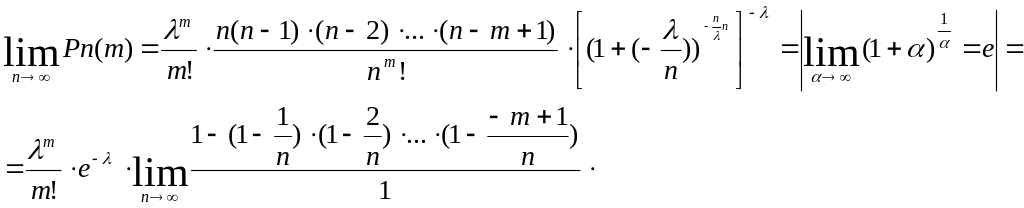
Интегральная теорема Лапласа Пусть вероятность наступления события в каждом испытании равна . В этом случае вероятность наступления события в испытаниях от до раз определяется по формуле

, , .

- функция Лапласа. Она также табулирована, но в разных учебниках вводится по-разному. В таблицах нет значений больше 5, при

Докажем что функция Лапласа нечетная:

.
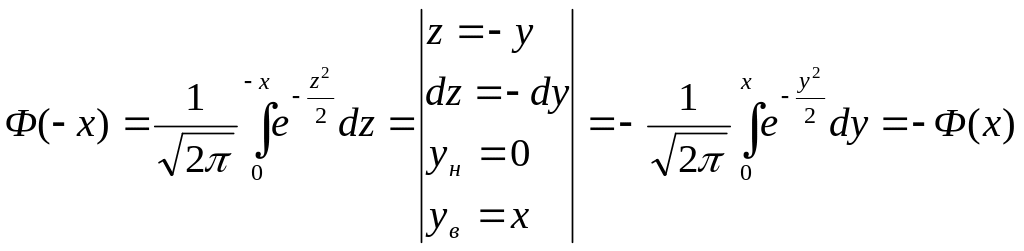