Независимые и зависимые события. Условная вероятность.

Два события называются независимыми, если вероятность появления одного из них не зависит от появления или непоявления другого события и зависимыми в противоположном случае.

Пример 1.8. Пусть в ящике 10 ламп, 3 из которых неисправны. Рассмотрим два варианта проверки ламп:

а) после проверки лампа возвращается в ящик;

б) после проверки лампа не возвращается в ящик.

Пусть с. - выбор неисправной лампы в первом опыте;

с. - выбор неисправной лампы во втором опыте.

Установить зависимость указанных событий при каждом варианте проверки.

Решение:

а)

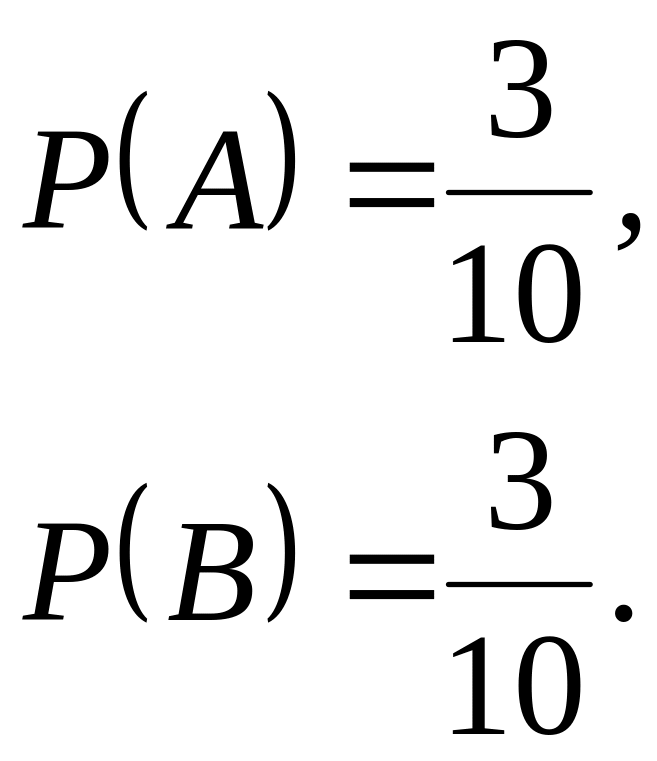
События и - независимые.

б) Пусть с. наступило, тогда .

Если же наступило с. , тогда .

Значит, события и - зависимые.

Для числа событий больше двух вводятся два понятия независимости события.

Несколько событий называются попарно независимыми, если каждые два из них независимые.

Несколько событий называются независимыми в совокупности, если каждые два из них попарно независимые и каждое из событий и произведения любого числа оставшихся событий также являются независимыми.

Условная вероятность события - это вероятность этого события, вычисленная при условии, что событие произошло.

Обозначаются или .

Теорема умножения для независимых событий

Вероятность произведения двух независимых событий равна произведению вероятностей этих событий:

.

Доказательство:

Пусть для события : - общее число исходов, - число благоприятствующих исходов, тогда .

Аналогично, и для события : .

Для события : , , тогда .

Следствие: вероятность произведения нескольких независимых в совокупности событий равно произведению вероятностей этих событий:

.

Пример 1.9. Вероятность попадания в мишень для первого стрелка равна 0,9, а для второго – 0,8. Найти вероятность того, что мишень поражена.

Решение: с. - мишень поражена

с. - мишень поражена -ым стрелком, .

,

, причем и - совместные события, поэтому доказанная выше теорема неприменима.

с. - мишень не поражена

, причем и - независимые события.

,

.

Теорема вероятности появления хотя бы одного события

Пусть события , … образуют полную группу несовместных событий и могут наступить с вероятностями , … . Пусть эти события независимы в совокупности.

Обозначим эти события через - событие, заключающееся в появлении хотя бы одного из указанных событий.

.

Пример1.9 решался с неявным использованием данной теоремы, так как событие «мишень поражена» тоже самое событие, что и событие «в мишени хотя бы одна пробоина».

Теорема умножения для зависимых событий

Вероятность произведения двух событий равна вероятности одного из них, умноженной на условную вероятность другого события, вычисленную при условии, что первое событие имело место:

.

Доказательство:

Пусть - общее число исходов, из которых благоприятствуют событию . Из этих исходов благоприятствуют также событию .

.

Аналогично доказывается, что .

Можно доказать, что

.

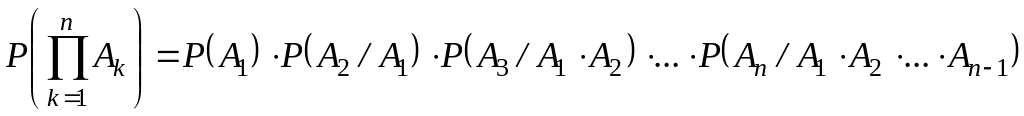Пример 1.10. Студент знает один билет из 30. Каким по счету он должен пойти, чтобы вероятность вытащить нужный билет была наибольшей?

Решение: с. – наш студент пошел -ым по счету и вытащил нужный билет, .

с. - -ый студент вытащил нужный билет.

, .

( и - зависимые события),

.

,

.

……

Ответ: Вероятность вытащить искомый билет не зависит от того, каким по счету идти.