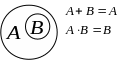Конспект лекций по дисциплине «Теория вероятностей и математическая статистика»

для студентов заочной формы обучения

Составители: Гладков Л.Л., Гладкова Г.А.

Поскольку на составление конспекта было отведено мало времени, в тексте возможны опечатки и неточности. Будем благодарны внимательным читателям, которые укажут на них.

Введение

Под случайными явлениями будем понимать явления, которые при многократном повторении в одинаковых условиях протекают по-разному.

Предметом теории вероятностей являются специфические закономерности, которые имеют место при массовых случайных явлениях, протекающих в одинаковых условиях.

Основными понятиями теории вероятностей являются:

• опыт;

• событие;

• вероятность.

Событие – всякое явление, которое может произойти или не произойти в результате опыта.

События подразделяются на:

• достоверные;

• невозможные;

• случайные.

Достоверное событие–обязательно произойдет в результате опыта,

невозможное – не может произойти в результате опыта,

случайное – может произойти или не произойти в результате опыта.

Раздел 1. Случайные события Виды случайных событий

События называются совместными, если появление одного из них не исключает появление других событий, и несовместными, если появление одного из них исключает появление остальных событий.

События обозначаются заглавными латинскими буквами с начала алфавита ( , , …).

Пример 1.1.

в течение одной экзаменационной сессии

A и B – несовместные события.

A и С, B и С – совместные события.

Равновозможными называются события, ни одно из которых не является более возможным, чем остальные (например, подбрасывание ровной монеты).

Группа событий называется полной группой, если в результате опыта обязательно наступит одно из событий, входящих в эту группу.

Противоположными называются два несовместных события, образующих полную группу Событие, противоположное событию А, обозначается (читается «не »).

Алгебра событий

Под суммой нескольких событий будем понимать появление хотя бы одного из этих событий.

Произведение нескольких событий – это событие, заключающееся в появлении всех этих событий.

Пример 1.2.

Определение вероятностей событий

Вероятность ( ) – это численная мера степени объективных возможностей наступления рассматриваемого события.

За нуль принята вероятность невозможного события, за единицу – достоверного, а вероятность случайного события составляет долю единицы:

.

Классическое определение вероятности

Пусть имеется равновозможных несовместных событий, образующих полную группу, каждое из них называются элементарным исходом опыта. Те исходы, при которых наступает интересующее нас событие называются благоприятствующими этому событию.

Вероятностью называется отношение числа благоприятствующих рассматриваемому событию исходов к общему числу всех равновозможных несовместных исходов , образующих полную группу:

.

Пример 1.3. Найти вероятность того, что при подбрасывании кубика выпадает

1. четная цифра;

2. при двух бросках 12 очков;

3. при двух бросках 11 очков.

Решение:

1) , , ;

2) т.к. любой из 6 цифр на первом кубике соответствует 6 вариантов выпадения цифры на втором кубике .