Числовые характеристики системы двумерных св

Запишем формулы для основных числовых характеристик

а) дискретных CВ

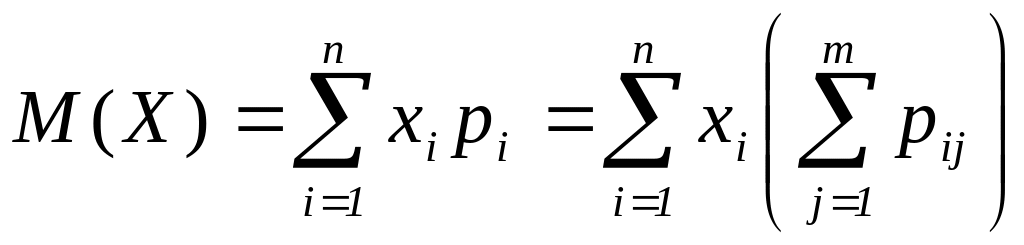
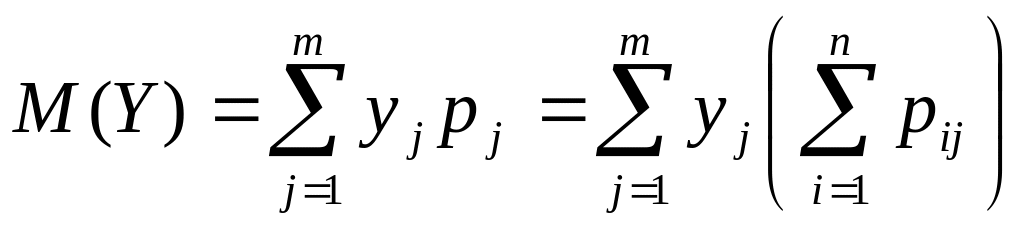
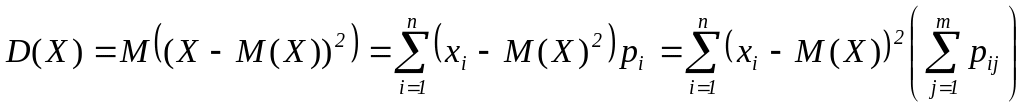
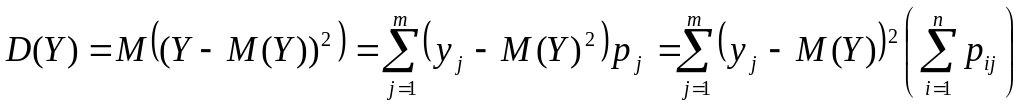
б) непрерывных CВ

Корреляционный момент. Коэффициент корреляции

Эти числовые характеристики описывают силу (степень) связи между СВ.

К орреляционным моментом CВ Х и Y называется математическое ожидание произведения отклонения этих CВ от их математического ожиданий

(1)

Если , то корреляцию называют положительной. Если , то корреляцию называют отрицательной.

В случае положительной корреляции имеет место следующая тенденция: с увеличением Х можно ожидать увеличения Y. (Х-рост студента, Y-вес студента, , т.е. с увеличением Х можно ожидать увеличения Y).

(2)

Если - корреляционный момент CВ на саму себя.

Обычно для вычисления использует вторую формулу.

Для дискретных CВ .

Для непрерывных CВ .

Для независимых Х и Y: , , и Х и Y называются некоррелированными СВ.

Обратное убеждение (если , то Х и Y –независимы) в общем случае неверно.

Если , то cв х и y называются некоррелированными, в противном случае ( )- коррелированными.

Можно показать,что .

Недостатки корреляционного момента :

1. Числовая характеристика описывает не только силу связи между Х и Y, но и степень разброса. Сила связи Х и Y может быть велика, но если разброс одной из CВ мал ( 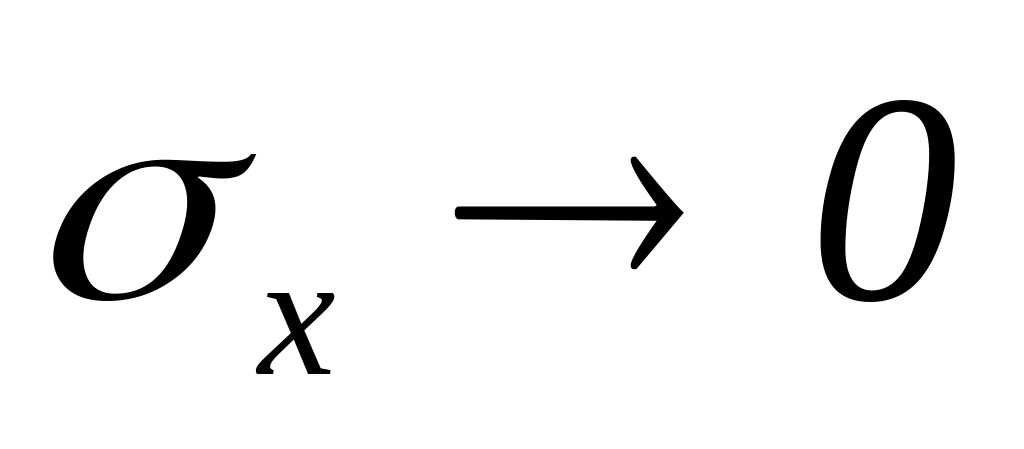), также может быть мал.

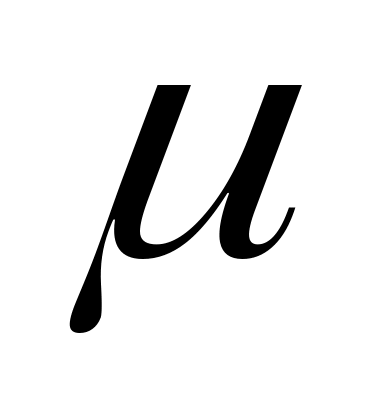2. имеет размерность, равную произведению размерности 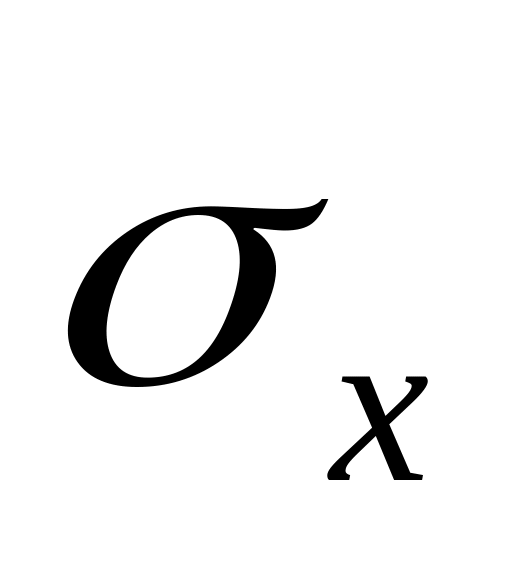на .

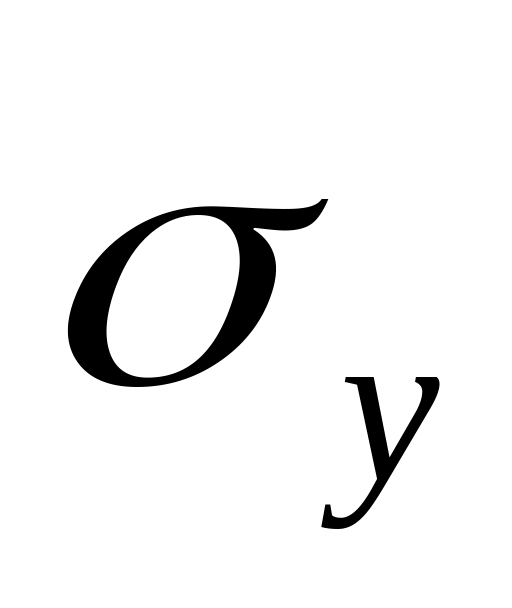Чтобы устранить оба недостатка, разделим на и получим безразмерную величину - коэффициент корреляции

, причем только когда между Х и Y имеется функциональная линейная зависимость , -const.

На практике Х и Y считаются достаточно коррелированными, если

.

Пример 3.8. Двумерная дискретная CВ задана таблицей. Найти , .

X Y	0	1
2	0,4	0,1		0,5
4	0,1	0,4		0,5
	0,5	0,5		1 1

;

;

, ;

;

, ;

;

;

.

11