Раздел 3 системы случайных величин

Часто случайное явление описывается несколькими СВ, при этом недостаточно изучать отдельные СВ, а необходимо учитывать связь между ними. Если рассматриваются совместно две СВ, то их называют двумерной СВ или системой двух случайных величин, три СВ – трехмерной СВ и т.д. Систему из n СВ называют n-мерной СВ.

Двумерная СВ обозначается (Х,Y), а ее значение (x, y); геометрически двумерную СВ удобно представлять как случайная точку на плоскости или случайный вектор, проведенный из начала координат в точку (Х,Y).

Закон распределения системы СВ – это соотношение между возможными значениями всех СВ, входящих в систему и вероятностями их появления.

Для дискретных двумерных СВ закон удобно представлять в виде таблицы с двумя входами, причем 1-ая цифра дает номер столбца, 2-ая-номер строки.

X Y			…			…
			…	…		…
			…	…		…
…	…	…	…	…	…	…	…		…
			…	…		…
…	…	…	…	…	…	…	…		…
			…	…		…
			…	…		…			1 1

- условие нормировки.

Просуммировав вероятности первой строки, получим вероятность того, что Y – примет значение , ; просуммировав вероятности i-ого столбца- .

Первый и последний столбец в данной таблице дают закон распределения для составляющей Х, а первая и последняя строки – закон распределения для CВ Y.

Пример 3.1. По мишени производится два выстрела. Вероятность попадания при каждом 0,7. Составить законы распределения для системы CВ (X,Y) и их составляющих X и Y, где X- число попаданий, Y-число промахов.

X Y	0	1	2
0	0	0	0,49		0,49
1	0	0,42	0		0,42
2	0,09	0	0		0,09
	0,09	0,42	0,49		1 1

Решение:

За исключением событий (Х=2, Y=0), (Х=1, Y=1) и (Х=0, Y=2) остальные события – невозможные. Поэтому их вероятности равны нулю.

Введем события - попадания при первом и втором выстреле, соответственно (р=0,7).

Событие - одно попадание, один промах.

, .

( и , и -независимые; и несовместные)

Интегральная функция распределения двумерной CВ – это вероятность того, что CВ Х примет значение меньше , а CВ Y примет значение меньше .

Из рисунка видно, что - это вероятность попадания случайной точки в бесконечный квадрат, расположенный левее и ниже тчки с координатами .

Свойства :

1. область изменения ;

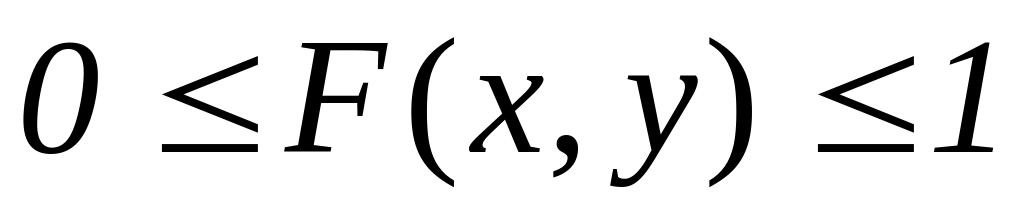2. предельное свойство ,

,

,

;

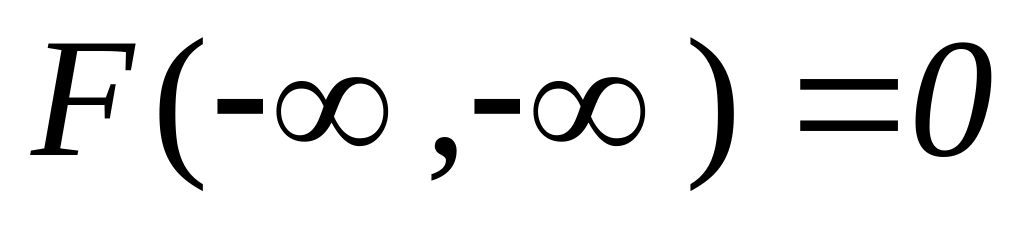3. является неубывающей функцией по аргументам .

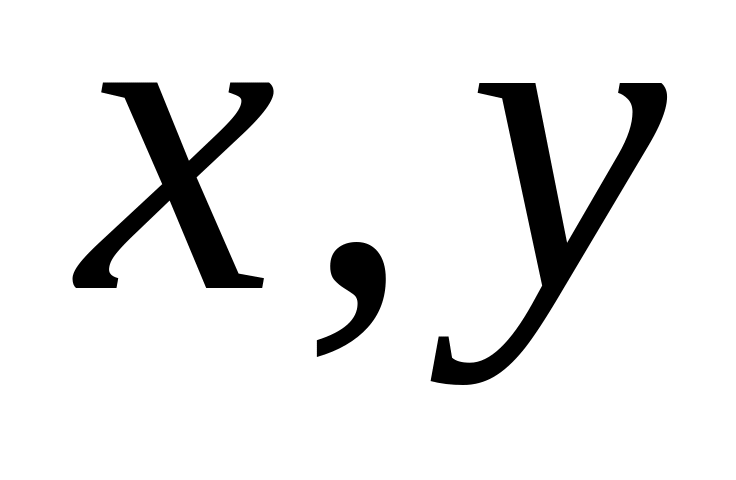4. вероятность попадания случайной точки в прямоугольник

Замечание:

Для непрерывной двумерной CВ вероятность того, что двумерная CВ примет одно конкретное значение

(вероятность попадания в линию равна нулю)

Пример3.2. Система СВ (Х,Y) распределена равномерно внутри квадрата со стороной . Построить .

Решение:

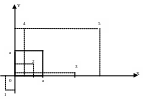
Воспользуемся классическим определением вероятности (геометрической интерпретацией).