Министерство образования и науки Российской Федерации

Пензенский государственный университет

Кафедра «Высшей и прикладной математики»

Отчет по преддипломной практике на тему:

«Особенности параллельных вычислений на видеокартах»

Выполнила: ст. гр. 07ЕП1:

Баулина О.А., Руководитель практики: Бойков И.В.

Дипломный руководитель: Захарова Ю.Ф.

Пенза, 2012

Содержание

Введение…………………………………………………………………………...3 1 Постановка задачи и последовательные ее методы решения………………..5

1.1 Задача Дирихле……………………………………………………………...5

1.2 Метод простых итераций…......………………………………………….....8

1.3 Методы Якоби……………………………………………………………….8

1.4 Методы Зейделя и его модификации………………………………………9

2 Параллельные методы решения задачи Дирихле для систем с общей памятью…………………………………………………………………………..11

2.1 Использование OpenMP для организации параллелизма……………….11

2.2 Проблема синхронизации параллельных вычислений…………………..12

2.3 Возможность неоднозначности вычислений в параллельных программах……………………………………………………………………..14

2.4 Исключение неоднозначности вычислений……………………………...15

2.5 Волновые схемы параллельных вычислений…………………………….17

3 Параллельные вычисления с использованием видеокарты…………………22

3.1 Общие сведения о GPU и NVIDIA CUDA ……………………………….22

3.1.1 Разница между CPU и GPU в параллельных расчётах………………22

3.1.2 Первые попытки применения расчётов на GPU……………………..26

3.1.3 Возможности NVIDIA CUDA…………………………………………29

3.1.4 Области применения параллельных расчётов на GPU………………33

3.2 Аппаратная и программная реализация CUDA………………………….35

3.2.1 Состав NVIDIA CUDA…………………………………………………35

3.2.2 Архитектура GPU………………………………………………………36

3.2.3 Модель программирования CUDA: потоковая модель……………...39

3.2.4 Модель программирования CUDA: модель памяти…………………42

3.3 Расширение языка c……………………………………………………….46

3.3.1 Директива вызова ядра……………………………………………….50

3.3.2 Основы CUDA host API………………………………………………51

3.3.3 Работа с памятью в CUDA…………………………………………...53

3.3.4 Использование событий для синхронизации на CPU……………...54

3.3.5 Получение информации об имеющихся GPU и их возможностях..55

3.3.6 Компиляция…………………………………………………………...57

Заключение……………………………………………………………………….58

Список используемых источников……………………………………………..59

Введение

С тех пор, как на графических процессорах стали доступны неграфические вычисления, многое изменилось. Можно найти не один пример того, как кластер из нескольких машин с мощными видеокартами мог поспорить с бешено дорогими суперкомпьютерами. И по сей день продолжается эволюционирование вычислений от «централизованной обработки данных» на центральном процессоре до «совместной обработки» на CPU (центральный процессор) и GPU (графический процессор). Для реализации новой вычислительной парадигмы компания NVIDIA изобрела архитектуру параллельных вычислений CUDA, на данный момент представленную в графических процессорах GeForce, ION, Quadro и Tesla и обеспечивающую необходимую базу разработчикам программного обеспечения.

CUDA (Compute Unified Device Architecture) – это технология, предназначенная для разработки приложений для массивно-параллельных вычислительных. Основными плюсами CUDA являются ее бесплатность, простота и гибкость.

Цель работы заключается в изучении особенностей параллельных вычислений на видеокартах. Исследовать эту задачу будем на примере решения эллиптического уравнения. Данный выбор обусловлен тем, что среди всех типов уравнений математической физики эллиптические уравнения с точки зрения вычислителей стоят особняком. Для численного решения подобных задач обычно применяется метод конечных разностей (метод сеток). Объем выполняемых при этом вычислений как правило является значительным, а графические процессоры в свою очередь предназначены для вычислений с большим параллелизмом и интенсивной арифметикой и демонстрируют хорошие результаты в том случае, когда с одной и той же последовательностью действий обрабатывает большой объём данных.

1 Постановка задачи и последовательные методы ее решения

В качестве классического представителя уравнений эллиптического типа рассмотрим уравнение Пуассона

(1.1) частным случаем которого является уравнение Лапласа . В общем случае дифференциальный оператор - функция источников.

Как известно, задача Коши для эллиптических уравнений некорректна, и для них может быть поставлена только краевая задача. Ограничиваясь далее двухмерным случаем, в качестве таковой будем рассматривать в некоторой замкнутой области D с границей Г задачу Дирихле

(1.2)

где s – расстояние вдоль Г, когда на границе области задано значение искомой функции.

1.1 Задача Дирихле

В случае двухмерного уравнения Пуассона проблема аппроксимации дифференциальной задачи разностной не является столь очевидной. Если граница Г области определения решения D гладкая и функция в (1.2) тоже гладкая, то второй порядок аппроксимации уравнения гарантирует второй порядок точности решения. Если, однако, либо граница области, либо функции, заданные на границах, оказываются негладкими, то в решении задачи в окрестности особых точек возникают весьма существенные погрешности. Поэтому равномерная сетка и второй порядок аппроксимации по обеим переменным внутри области еще не обеспечивают решения задачи со вторым порядком точности. В таких случаях используют либо сгущение сетки в окрестности особенностей решения, либо предварительно выделяют эти особенности в виде аналитического решения задачи с последующей стыковкой его с численным решением в остальной области. Заметим, однако, что при определенной согласованности граничных условий и правой части уравнения в особых точках границы решение может оказаться гладким, и в этом случае дополнительных проблем с аппроксимацией задачи не возникает. Например, такая ситуация имеет место, если область D прямоугольная, а на Г непрерывная.

Перейдем теперь к задаче Дирихле. Для простоты изложения материала в качестве области задания D функции u(x₁,х₂) далее будет использоваться единичный квадрат с краевыми условиями первого рода на границе расчетной области, и все условия согласования, обеспечивающие гладкость решения, выполнены. Имеем:

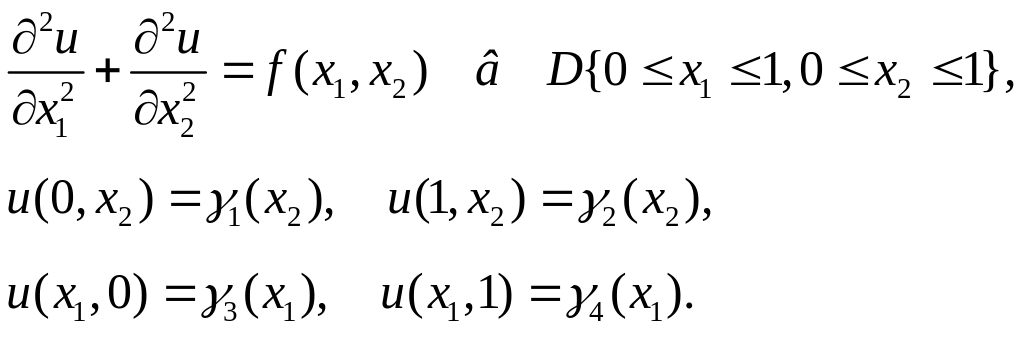
В области D построим прямоугольную сетку с шагами , и где , - целые положительные числа, и введем в узлах этой сетки сеточную функцию .

Рис. 1  Прямоугольная сетка в области D (темные точки представляют внутренние узлы сетки, нумерация узлов в строках слева направо, а в столбцах — сверху вниз)

Выбираем простейший пятиточечный шаблон разностной схемы "крест". Аппроксимируя вторые производные центральными разностями, имеем

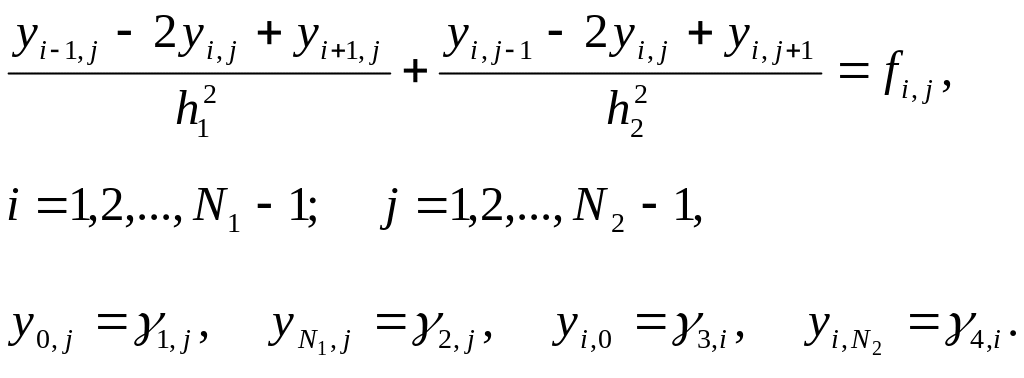(1.1.1)

Или в операторной форме ,

где

Для прямоугольной области полученную систему линейных алгебраических уравнений можно записать в векторно-матричной форме:

(1.1.2)

где

Система (1.1.2) имеет блочно-треугольную матрицу и может быть решена с помощью метода матричной прогонки. Однако он требует много затрат машинного времени и практически не применяется. Поэтому для решения (1.1.2) обычно используют итерационные методы. Рассмотрим некоторые из них.