Определение вероятностей отказа и обслуживания Основные формулы для смо Эрланга

Задаваемые параметры СМО:

n – количество каналов;

λ – интенсивность входящего потока;

μ – интенсивность обслуживания.

Вычисляемые параметры:

ρ – приведенная интенсивность, нагрузка СМО;

трафик:

ρ=λ/μ.

Формулы Эрланга определяют зависимости вероятностей состояний СМО, выраженные через количество каналов n и трафик ρ.

Вероятность того, что все каналы свободны

. (8.2)

Вероятность того, что заняты k каналов

. (8.3)

Вероятность того, что заняты все n каналов

. (8.4)

Вероятность отказа, т. е. вероятность того, что поступившая заявка найдет все каналы занятыми

Р_отк=Р_n . (8.5)

Вероятность обслуживания

Р_обс=1 – Р_отк . (8.6)

Пример расчетов по формулам Эрланга

Пусть многоканальная СМО с отказами имеет следующие параметры:

n=3, λ=20, μ=10

Требуется определить вероятности состояния системы. Система может находиться в четырех состояниях:

S₀ - все каналы свободны;

S₁ - занят один канал;

S₂ - заняты два канала;

S₃ - заняты три канала;

Граф состояний системы имеет вид, представленный на рис.8.2.

Рис. 8.2. Граф системы с четырьмя состояниями

Стрелки слева направо означают переход системы в более высокое состояние, которое вызывается воздействием входящего потока заявок, а справа налево – переход в более низкое состояние, которое вызывается воздействием потока обслуживания.

Вычисляем величину нагрузки системы

ρ=λ/μ=20/10=2 эрл.

В соответствии с формулами Эрланга имеем следующие вероятности.

Вероятность того, что все каналы свободны

.

Вероятность того, что заняты k каналов

.

В соответствии с этой формулой вероятности того, что заняты один, два или три канала равны

;

;

.

Поскольку система обязательно находится в одном из указанных состояний, должно выполняться условие

.

Имеем,

.

Вероятность того, что заняты все n каналов, определяется по формуле

.

Вероятность отказа

Р_отк=Р_n=0,211.

Вероятность обслуживания

Р_обс=1 – Р_отк=1 – 0,211=0,789.

Построение графиков вероятности отказа и обслуживания на основе расчетных данных

Анализируются характер зависимостей Р_отк(n) и Р_отк(ρ), а также Р_обс(n) и Р_обс(ρ).

Опорная точка (точка 1):

n =3, ρ =2.

Имеем:

Р₀₌0,158 Р₁₌0,316 Р₂₌0,316

Р₃₌0,211 Р_отк=0,211 Р_обс=0,789

Расчеты при изменении числа каналов (точка 2):

n =4, ρ=2

Пример расчета:

;

.

Имеем для точки 2 следующие результаты:

Р₀₌0,143 Р₁₌0,286 Р₂₌0,286

Р₃₌0,191 Р₄₌0,095 Р_отк=0,095 Р_обс=0,905

Сопоставление результатов расчетов Р_отк и Р_обс в точках 1 и 2 показывает, что с увеличением числа каналов с n=3 до n=4 вероятность отказа уменьшается с 0,211 до 0,095, а вероятность обслуживания увеличивается с 0,789 до 0,905.

Результаты расчетов при ρ=const и изменении n от 1 до 4 представлены в табл.8.1.

Таблица 8.1.

ρ	n	P0	P1	P2	P3	P4	Pотк	Робс
2	1	0.333	0.666				0,666	0,333
2	2	0.200	0.400	0.400			0,400	0,600
2	3	0.158	0.316	0.316	0.211		0,211	0,789
2	4	0.143	0.286	0.191	0.191	0.095	0,095	0,905

Характер графиков Р_отк и Р_обс показан на рис.8.3.

Рис. 8.3. Зависимость вероятностей отказа и обслуживания при изменении количества каналов с n=1 до n=5

Расчеты Р_отк и Р_обс при изменении приведенной интенсивности.

Пример расчета для точки 3 с n=3 и ρ=4:

;

.

Имеем для точки 3 следующие результаты:

Р₀₌0,042 Р₁₌0,168 Р₂₌0,336

Р₃₌0,451 Р_отк=0,451 Р_обс=0,549.

Сопоставление результатов расчетов Р_отк и Р_обс для точек 1 и 3 показывает, что с увеличением нагрузки системы с ρ=2 до ρ=4 вероятность отказа увеличивается, с 0,211 до 0,451, а вероятность обслуживания уменьшается с 0,789 до 0,549.

Результаты расчетов при n=const и изменении ρ от 1 до 4 представлены в табл.8.2.

Таблица 8.2.

ρ	n	P0	P1	P2	P3	Pотк	Робс
1	3	0,375	0,375	0,188	0,063	0,063	0,937
2	3	0,159	0,318	0,318	0,212	0,212	0,788
3	3	0,077	0,213	0,347	0,347	0,347	0,653
4	3	0,042	0,168	0,336	0,451	0,451	0,549

Характер графиков Р_отк и Р_обс показан на рис.8.4.

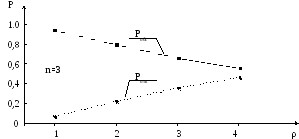
Рис. 8.4. Зависимость вероятностей отказа и обслуживания при изменении нагрузки на систему с ρ=1 до ρ=4