
- •Исчисления децильного коэффициента и коэффициента джини
- •Кривая Лоренца и ее использования для анализа степени имущественного неравенства...
- •В каких случаях кривая производственных возможностей (кпв) имеет вид прямой, а в каких случаях выпуклая?
- •Являются ли три фундаментальные проблемы экономики независимыми или у них одна общая причина?
- •Что производить?
- •Как производить?
- •Для кого производить?
- •Как обосновать производственный характер изокванты от графика производственной функции?
- •Данные по значению коэффициента джини и децильного коэффициента в России, Америке, Германии. Сравнить.
Исчисления децильного коэффициента и коэффициента джини
 Коэффициент
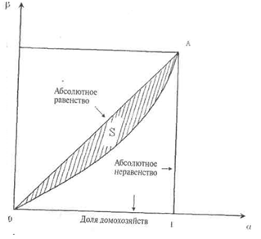
Джини - это измеритель неравенства
доходов, численно равный удвоенной
площади между линией абсолютного
равенства (отрезком ОА) и кривой Лоренца
(удвоенной площади фигуры S на рис.7.1,
а). Из данного определения следует, что
возможные значения коэффициента Джини
лежат в пределах от нуля до единицы.
Данный показатель равен нулю при
абсолютном равенстве доходов и близок
к единице при абсолютном неравенстве
доходов.
Коэффициент
Джини - это измеритель неравенства
доходов, численно равный удвоенной
площади между линией абсолютного
равенства (отрезком ОА) и кривой Лоренца
(удвоенной площади фигуры S на рис.7.1,
а). Из данного определения следует, что
возможные значения коэффициента Джини
лежат в пределах от нуля до единицы.
Данный показатель равен нулю при
абсолютном равенстве доходов и близок
к единице при абсолютном неравенстве
доходов.
Коэффициент концентрации Лоренца или индекс Джини (КL) дает возможность численно оценить степень неравенства. Для равномерного распределения он равен нулю, в условиях абсолютного неравенства он равен единице.
![]() Для
расчета коэффициента концентрации
Лоренца (индекса Джини) используется
следующая формула:
Для
расчета коэффициента концентрации
Лоренца (индекса Джини) используется
следующая формула:
где (Fi-Fi-1) - доля населения, относящаяся к i-ому интервалу,
Si-1, Si - доля суммарного дохода, приходящаяся на начало и конец i-ого интервала 6).
Коэффициент Джини (Gini coefficient) – это количественный показатель, показывающий степень неравенства различных вариантов распределения доходов, разработанный итальянским экономистом, статистиком и демографом Коррадо Джини (1884-1965 г.г.).
![]()
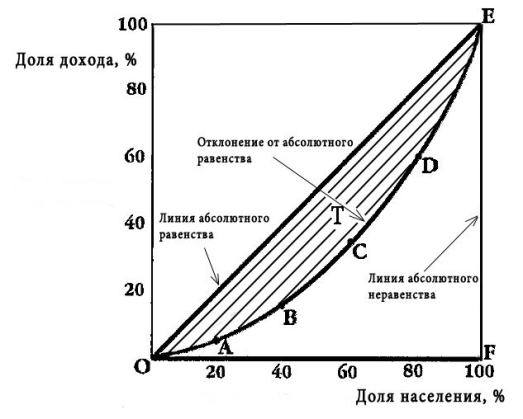
Линия OABCDE показывает фактическое распределение совокупного дохода. Заштрихованная площадь показывает степень неравенства в распределении доходов. Обозначим ее через Т. Разделив Т на площадь треугольника OEF, получим коэффициент Джини, показатель степени неравенства доходов.
Чем выше неравенство в распределении доходов, тем больше коэффициент приближается к единице (абсолютное неравенство). И чем выше равенство в распределении доходов, тем меньше данный коэффициент. При абсолютном равенстве он достигает нуля. Системы прогрессивного налогообложения и трансфертных платежей приближают "кривую Лоренца" к биссектрисе. Опыт развитых стран свидетельствует, что неравенство в распределении доходов со временем сокращается. В нашей стране дифференциация доходов населения представлена в таблице (в сравнении с США).
![]() Децильный
коэффициент дифференциации
(Kd)
рассчитывается как отношение уровней,
ниже и выше которых находятся десятые
доли совокупности в разных концах
распределения по уровню доходов: Kd
= d9/d1
Децильный
коэффициент дифференциации
(Kd)
рассчитывается как отношение уровней,
ниже и выше которых находятся десятые
доли совокупности в разных концах
распределения по уровню доходов: Kd
= d9/d1
где
Ud1,9 - определяется по таблице значений функций нормального распределения для значений 0,1 и 0,9 соответственно,
d1 - значение аргумента (в данном случае дохода), вероятность быть ниже которого равна 0,1 (F1) (т.е. 10% населения имеют доход ниже этого значения),
d9 - значение аргумента, вероятность быть ниже которого равна 0,9 (F9) (т.е. 10% населения имеют доход выше этого значения).
Кривая Лоренца и ее использования для анализа степени имущественного неравенства...
Кривая Лоренца представляет собой кумулятивное распределение численности населения и соответствующих этой численности доходов. В результате она показывает соотношение процентов всех доходов и процентов всех их получателей.
Если бы доходы распределялись равномерно, т.е. 10% получателей имели бы десятую часть доходов, 50% - половину и т.д., то такое распределение имело бы вид линии равномерного распределения (диагонали квадрата со сторонами от 0% до 100%). Неравномерное распределение характеризуется кривой Лоренца (линией фактического распределения), отстоящей от прямой тем дальше, чем больше дифференциация.
Кривая Лоренца - это ломаная, которая состоит из отрезков, соединяющих соседние точки (аi; bi). Число отрезков, составляющих ломаную, равно числу исследуемых домохозяйств. Если число домохозяйств весьма велико (например, когда исследуется дифференциация доходов в стране), кривая Лоренца принимает форму плавной дугообразной линии.
Кривая Лоренца обладает следующими свойствами:
ее концами служат точки О (0; 0) и А (1;1);
она является восходящей кривой, расположенной под биссектрисой первого координатного угла;
при равном распределении доходов она совпадает с отрезком ОА;
при абсолютно неравномерном распределении доходов (когда доход всех домохозяйств, кроме одного, равен нулю) она состоит из двух отрезков, один из которых лежит на оси абсцисс. Чем больше число домохозяйств, тем ближе угол между этими отрезками к прямому углу;
чем больше степень неравенства доходов, тем больше площадь между кривой Лоренца и биссектрисой первого координатного угла ОА. Данное свойство кривой Лоренца позволяет дать геометрическую интерпретацию коэффициента Джини.
