4.7 Аналіз часових рядів і прогнозування

Завданням цього розділу статистичного дослідження є аналіз розвитку соціально-економічних явищ. Перелік статистичних показників, динаміку яких вивчають, вказано в додатку З. Керівник роботи визначає конкретний показник в залежності від теми роботи і вказує його у завданні на курсову роботу.

Розраховуємо аналітичні та середні характеристики ряду динаміки.

Абсолютні прирости:

Ланцюгові	Базисні

Коефіцієнти росту:

Ланцюгові	Базисні

Темпи росту

Ланцюгові	Базисні

Темпи приросту

Ланцюгові	Базисні

Абсолютне значення 1 % приросту

Результати розрахунків слід представити в табл. 4.5

Таблиця 4.5 – Аналітична характеристика динаміки обраного показника

Пе- ріод	Абсо- лютні прирос- ти, млн.грн.		Коефі- цієнти росту		Темпи росту, %		Темпи прирос- ту, %		АЗ, млн.грн.
	ланцюгові	базисні	ланцюгові	базисні	ланцюгові	базисні	ланцюгові	базисні

Середні характеристики ряду динаміки:

Середній рівень динамічного ряду:

- для інтервальних динамічних рядів з рівними інтервалами ;

- для моментних динамічних рядів з рівними інтервалами

.

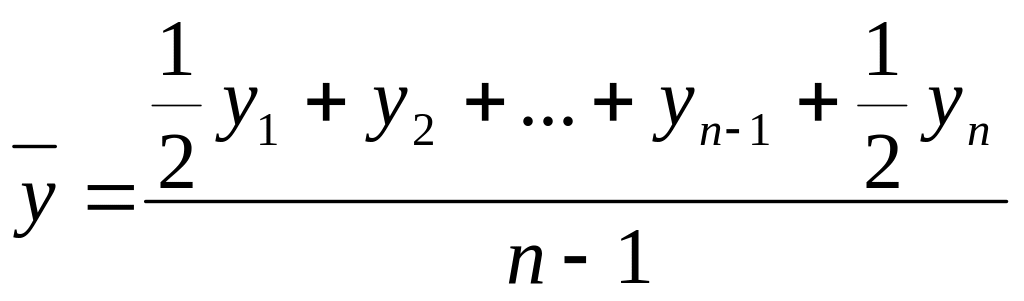Середній абсолютний приріст:

.

Середній коефіцієнт росту:

Середній темп приросту:

Виявляємо основну тенденцію розвитку.

Виявляємо тенденцію середнього рівня та тенденцію дисперсії за видами методом порівняння середніх рівнів ряду.

Для цього розділимо ряд на дві частини: n₁=2, n₂=3. По кожній частині ряду розрахуємо середні і дисперсії .

Перевіримо гіпотезу про рівність дисперсій для рівня значущості :

Нульова гіпотеза Но:

Альтернативна гіпотеза Н₁:

Коли

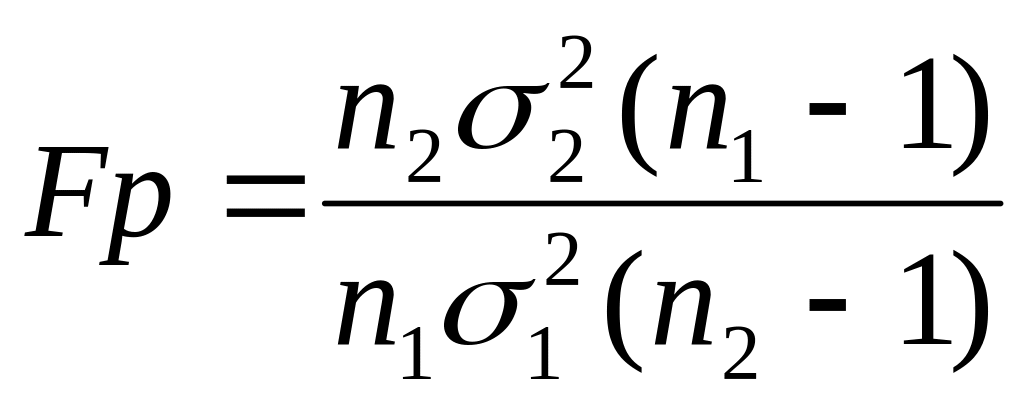
F(0,95; n1-1; n2-1)=F(0,95; 2-1; 3-1)=200.

Якщо розрахункове значення F-критерію Фішера є меншим за критичне, нульва гіпотеза про рівність дисперсій не відкидається, дисперсії відрізняються незначуще, розходження між ними носять випадковий характер, тенденція дисперсії не існує.

Перевірку основної гіпотези про рівність середніх рівнів двох сукупностей n₁ та n₂ здійснимо на основі t-критерію Стьюдента.

Нульова гіпотеза Но:

Альтернативна гіпотеза На:

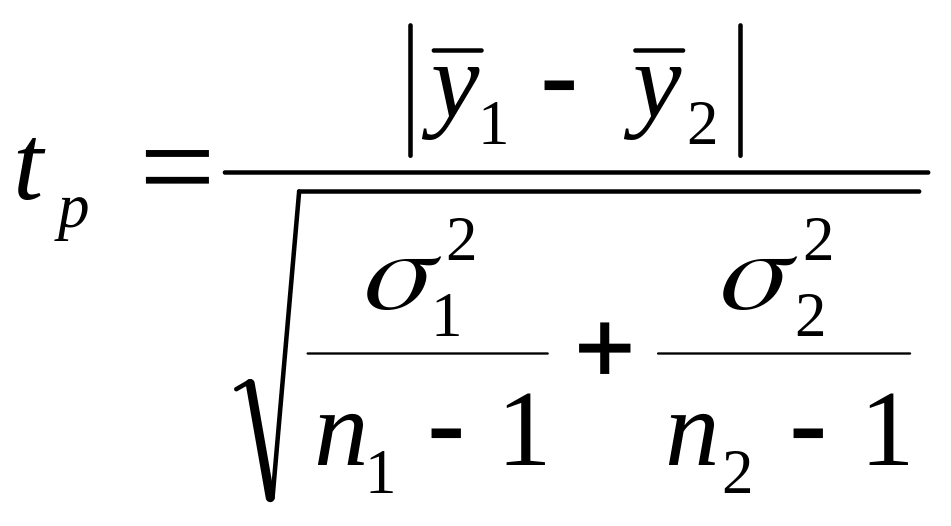
t(0,95; v=n1+n2-2=2+3-2=3)=3,182

Якщо розрахункове значення t-критерію Стьюдента є меншим за критичне, розходження між розрахованими середніми неістотне, отже, тенденції середньої не існує.

Вирішення цього питання може бути здійснене при повторній перевірці результатів методами виявлення тенденції не за її видами, а в цілому в ряді динаміки. З цією метою можна використати фазочастотний критерій знаків різниць Валліса та Мура.

Розрахункове значення фазочастотного критерію різниць визначають за формулою:

,

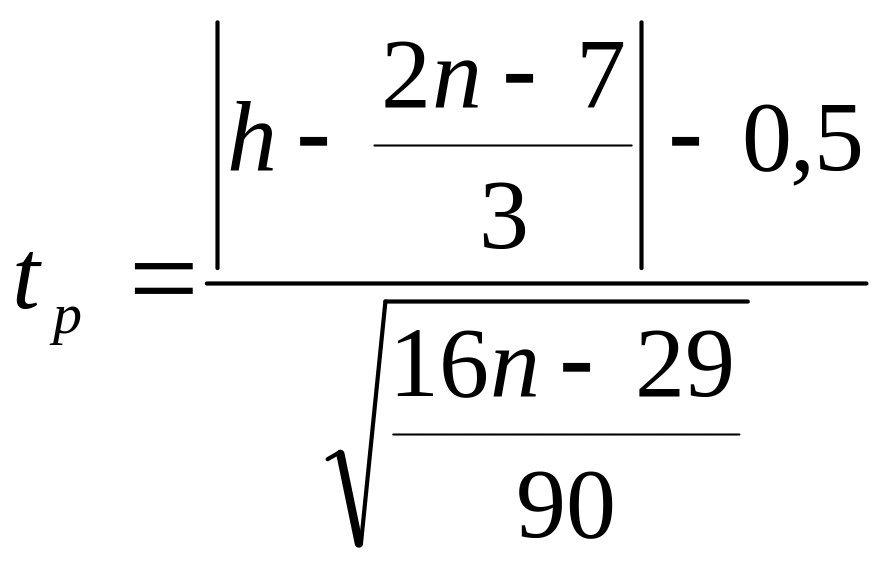де h – число фаз, n – число рівнів.

Якщо розрахункове значення фазочастотного критерію перевищує критичне, то нульова гіпотеза про те, що знаки абсолютних ланцюгових приростів утворюють випадкову послідовність, відкидається, рівні ряду динаміки не утворюють випадкову послідовність, отже, мають тенденцію.

Коли наявність тенденції виявлено, визначаємо основну тенденцію розвитку і її напрямок на основі методу аналітичного вирівнювання.

Вибір функції здійснимо методом перебору ряду функцій та вибору тієї, якій відповідає найменша середня квадратична похибка та середня похибка апроксимації. Для описування тенденції використаємо пряму, параболу другого порядку та показникову функцію.

Рівняння прямої: Y=а₀+а₁t

Параметри лінійного тренду знайдемо з наступної системи нормальних рівнянь:

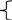
Розрахуємо параметри лінійного тренду спрощеним методом ;

Зобразимо динаміку явища та лінійний тренд графічно.

Рівняння параболи другого порядку: Y=a₀+a₁t+a₂t²

Параметри нелінійного тренду – параболи другого порядку знайдемо з наступної системи нормальних рівнянь:

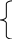
Розрахуємо параметри нелінійного тренду – параболи другого порядку спрощеним методом

Зобразимо динаміку явища та нелінійний тренд – параболу другого порядку графічно.

Рівняння показникової функції Y=a₀a₁^t

Для визначення параметрів нелінійного тренду – показникової функції прологарифмуємо рівні, після чого логарифми показникової функції описуються лінійною функцією: lg Y=lg a₀+t lg a₁

Система нормальних рівнянь має вигляд:

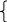
Коли , розв‘язок системи рівнянь спрощується.

Зобразимо динаміку явища та нелінійний тренд – показникову функцію графічно.

Середня квадратична похибка:

Середня похибка апроксимації:

Адекватність кожної функції визначають на основі середньої похибки апроксимації. Після того, як виявлена тенденція і визначений її напрямок, приступають до прогнозування показника на наступні два роки найпростішими методами та методом екстраполяції на основі обраної функції.

Зробимо прогноз найпростішими методами середнього абсолютного приросту та середнього темпу росту

Методом середнього абсолютного приросту модель прогнозу має вигляд:

,

де L- період випередження

Прогнозування методом середнього абсолютного приросту можливе при виконанні умови:

, де ; .

Методом середнього темпу росту модель прогнозу має вигляд:

,

де L- період випередження.

Порівнявши моделі прогнозу за різними методами на основі середньої квадратичної похибки, робимо висновок, прогноз за яким методом є найбільш точним

Якщо варіація часового ряду має сезонний характер, користуються для прогнозування моделями з виділеним трендом і сезонною компонентою. Точність прогнозу визначають на основі середньої квадратичної похибки.

Для спостереження економічного ряду даних і його прогнозування можна працювати в модулі Statistica Time Series / Forecasting (Аналіз часових рядів і прогнозування).