1. Электрофизические свойства полупроводников.

( возникновение свободных носителей заряда в полупроводниках I-,n- и p- типа ).

1.1 Носители заряда — общее название подвижных частиц или квазичастиц, которые несут электрический заряд и способны обеспечивать протекание электрического тока.

Примерами подвижных частиц являются электроны, ионы. Примером квазичастицы-носителя заряда является дырка.

Чаще всего термин «носители заряда» применяется в физике твёрдого тела и физике полупроводников.

В полупроводниках носителями заряда являются электроны и дырки. Отношение их концентраций определяет тип проводимости полупроводника. Те носители, концентрация которых выше, называют основными носителями заряда, а носители другого типа — неосновными.

Если концентрация электронов значительно превосходит концентрацию дырок, то такой полупроводник называют полупроводником n-типа проводимости. В этом случае основными носителями заряда являются электроны, а неосновными носителями — дырки.

Соответственно, если концентрация дырок выше, чем электронов, то полупроводник называют полупроводником p-типа. В нем основными носителями являются дырки, а неосновными носителями — электроны.

Концентрация равновесных носителей заряда в полупроводнике определяется только температурой образца и концентрацией легирующих примесей. Под действием внешних воздействий (инжекция, облучение образца светом, ионизирующими частицами или ионизирующим излучением) в полупроводнике возникают неравновесные носители заряда, и полная концентрация носителей заряда увеличивается.

2. Концентрации свободных носителей заряда.

Образование свободных носителей заряда в полупроводниках связано с переходом электронов из валентной зоны в зону проводимости. Для осуществления такого перехода электрон должен получить энергию, достаточную для преодоления запрещенной зоны. Эту энергию электрон получает от ионов решетки, совершающих тепловые колебания. Концентрация носителей заряда, вызванная термическим возбуждением в состоянии теплового равновесия, называется равновесной.Однако, помимо теплового возбуждения, появление свободных носителей заряда может быть связано с другими причинами, например в результате облучения фотонами или частицами большой энергии, ударной ионизации, введения носителей заряда в полупроводник из другого тела (инжекция) и др. Возникшие таким образом избыточные носители заряда называются неравновесными. Процесс введения неравновесных носителей заряда называют инжекцией. Таким образом, полная концентрация носителей заряда равна:

	(11.1)
	(11.2)

где n₀ и p₀ – равновесная концентрация, а n и p – неравновесные концентрации электронов и дырок. Если возбуждение избыточных электронов производилось из валентной зоны, полупроводник однородный и не содержит объемного заряда, то концентрация избыточных электронов равна концентрации избыточных дырок:

.

(11.3)

2. Энергетические зоны.

Энергетические зоны -квазинепрерывная совокупность одночастичных состояний в энергетич. спектре конденсированной среды (в частности, твёрдого тела). Возникновение зон можно объяснить, рассматривая либо движение частицы в периодич. поле (приближение слабой связи), либо модификацию энергетич. уровней атомов при их сближении (приближение сильной связи, см. Зонная теория). Простейший вариант объяснения состоит в том, что при сближении N одинаковых атомов происходит расщепление каждого уровня на N подуровней вследствие перекрытия электронных оболочек атомов. Если число N очень велико (N ), то расстояния между подуровнями стремятся к 0. Это и означает возникновение Э. з. При введении в кристалл примесных атомов (концентрация к-рых такова, что возможно перекрытие их электронных оболочек) могут возникать новые Э. з. (примесные зоны). В условиях, когда на движение электрона оказывают влияние его границы (плёнки) или внеш. поля, Э. з. расщепляются на ряд подзон (п о д з о н ы Л а н д а у в квантующем магн. поле, м и н и з о н ы в сверх решётках и т. п.). Стационарное состояние электрона в конденсиров. среде характеризуется номером Э. з., в к-рой он находится, и квантовым числом, определяющим положение электрона в этой зоне (напр., в кристалле- квазиимпульсом).

1.4 Распределение Форми-Дирака.

Статистика Фе́рми — Дира́ка в статистической физике — квантовая статистика, применяемая к системам тождественных фермионов (как правило, частиц с полуцелым спином, подчиняющихся принципу запрета Паули, то есть, одно и то же квантовое состояние не может занимать более одной частицы); определяет распределение вероятностей нахождения фермионов на энергетических уровнях системы, находящейся в термодинамическом равновесии; предложена в 1926 году итальянским физиком Энрико Ферми и одновременно английским физиком Полем Дираком, который выяснил её квантово-механический смысл; позволяет найти вероятность, с которой фермион занимает данный энергетический уровень.

Работы по статистике Ферми — Дирака были опубликованы в 1926 году, а в 1927 она была применена Арнольдом Зоммерфельдом к электронам вметалле.

В статистике Ферми — Дирака среднее число частиц в состоянии с энергией   есть

где

 — среднее число частиц в состоянии  ,

 — энергия состояния  ,

 — кратность вырождения состояния   (число состояний с энергией  ),

 — химический потенциал (который равен энергии Ферми   при абсолютном нуле температуры),

 — постоянная Больцмана,

 — абсолютная температура.

(ферми-распре-деление) - ф-ция распределения по уровням энергии тождественных частиц с полуцелым спином при условии, что взаимодействием частиц между собой можно пренебречь. Ф.- Д. р.- ф-ция распределения идеального квантового газа ( ферми-газа),подчиняющегося Ферми-Дирака статистике. Ф.- Д. р. соответствует максимуму статистического веса (или энтропии) с учётом неразличимости тождественных частиц .

5. Ток дрейфа.

1. В полупроводниках свободные электроны и дырки находятся в состоянии хаотического движения. Поэтому, если выбрать произвольное сечение внутри объема полупроводника и подсчитать число носителей заряда, проходящих через это сечение за единицу времени слева направо и справа налево, значения этих чисел окажутся одинаковыми. Это означает, что электрический ток в данном объеме полупроводника отсутствует.

2. При помещении полупроводника в электрическое поле напряженностью Е на хаотическое движение носителей зарядов накладывается составляющая направленного движения. Направленное движение носителей зарядов в электрическом поле обусловливает появление тока, называемого дрейфовым. Из-за столкновения носителей зарядов с атомами кристаллической решетки их движение в направлении действия электрического поля прерывисто и характеризуется подвижностью  . Подвижность равна средней скорости  , приобретаемой носителями заряда в направлении действия электрического поля напряженностью Е = 1 В/м, т. е.

3. . (1.11)

4. Подвижность носителей зарядов зависит от механизма их рассеивания в кристаллической решетке. Исследования показывают, что подвижности электронов  _n и дырок  _p имеют различное значение ( _n >  _p) и определяются температурой и концентрацией примесей. Увеличение температуры приводит к уменьшению подвижности, что зависит от числа столкновений носителей зарядов в единицу времени.

5. Плотность тока в полупроводнике, обусловленного дрейфом свободных электронов под действием внешнего электрического поля со средней скоростью  , определяется выражением  .

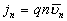6. Перемещение (дрейф) дырок в валентной зоне со средней скоростью   создает в полупроводнике дырочный ток, плотность которого  . Следовательно, полная плотность тока в полупроводнике содержит электронную j_n и дырочную j_р составляющие и равна их сумме (n и p — концентрации соответственно электронов и дырок).

7. Подставляя в выражение для плотности тока соотношение для средней скорости электронов и дырок (1.11), получаем

8. . (1.12)

9. Если сравнить выражение (1.12) с законом Ома j =  Е, то удельная электропроводность полупроводника определяется соотношением

10. .

11. У полупроводника с собственной электропроводностью концентрация электронов равна концентрации дырок (n_i = p_i), и его удельная электропроводность определяется выражением

12. .

13. В полупроводнике n-типа  >   , и его удельная электропроводность с достаточной степенью точности может быть определена выражением

14. .

15. В полупроводнике р-типа  >   , и удельная электропроводность такого полупроводника

16. 

17. В области высоких температур концентрация электронов и дырок значительно возрастает за счет разрыва ковалентных связей и, несмотря на уменьшение их подвижности, электропроводность полупроводника увеличивается по экспоненциальному закону.

1.6 Ток диффузии

ДИФФУЗИОННЫЙ ТОК , электродный ток в условиях, когда скорость электрохим. р-ции определяется скоростью подвода реагирующего в-ва к пов-сти электрода или отвода от этой пов-сти продуктов р-ции. Перенос реагирующих в-в в р-ре электролита может осуществляться по трем механизмам: диффузии, миграции и конвекции. Соотв. поток в-ва от электрода или к нему можно рассматривать как сумму диффузионной, миграционной и конвективной составляющих. Первая обусловлена наличием градиента концентрации в-ва с в направлении х от электрода в т. наз. диффузионном слое, где концентрация изменяется от значения в объеме жидкости до значения на пов-сти электрода за счет расходования из р-ра или образования в-ва в электрохим. р-ции. Вторая связана с миграцией ионов из-за наличия градиента электрич. потенциала дЕ/дх в диффузионном слое. Третья связана с переносом в-ва к электроду или от него потоком жидкости в межэлектродном пространстве. Скорость движения р-ра v уменьшается при приближении к электроду и в простейшем случае становится равной нулю на его пов-сти. Поэтому выражение для Д. т. содержит два слагаемых - диффузионное и миграционное. При этом v оказывает влияние на Д. т., изменяя толщину диффузионного слоя, т. е. градиенты концентрации и потенциала, к-рые увеличиваются при увеличении v. В разб. р-рах электролитов для плотности ij Д. т. частиц j-го сорта (катионов):