Класична механіка. . Глава 8. Релятивістська механіка. .

Рис. 7.5.

Ц

67

е забезпечує більшу відносну швидкість ламінарного руху повітря V₁ над крилом у порівнянні зі швидкістю руху повітря V₂ під крилом, що є наслідком рівняння нерозривності (7.6).

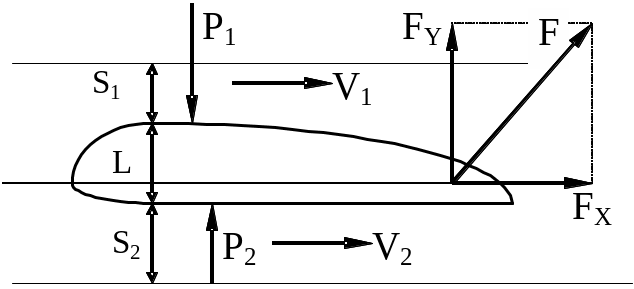
Для нашого випадку рівняння Бернуллі буде мати вигляд:

P₁ + ¹/₂ V₁² = P₂ + ¹/₂ V₂² , (7.16)

рис. 8.1.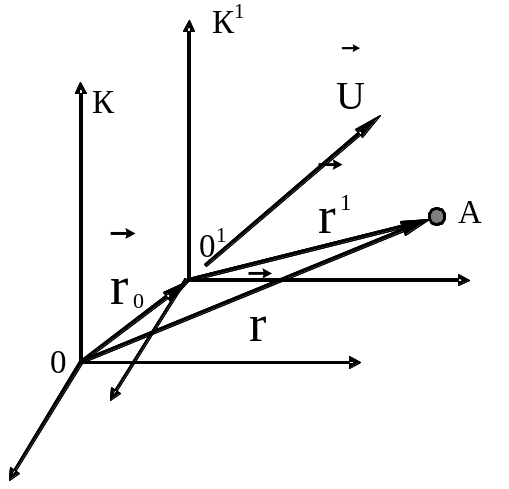

Тоді, врахувавши, що V₁ > V₂, з цього рівняння маємо Р₁ < Р₂. Тобто тиск повітря під крилом літака вищий, ніж над ним. Завдяки цьому і виникає підйомна сила крила, яка чисельно може бути обрахована за наступною формулою:

F_y = ¹/₂ C_y V² L , (7.17)

де С_у - коефіцієнт підйомної сили.

Відношення коефіцієнта С_у до коефіцієнта С_х отримало назву якість крила. Чім більша якість крила, тим краща його конструкція з точки зору аеродинаміки.

7.7. Контрольні завдання і запитання.

1. Сформулюйте закони Паскаля та Архімеда.

2. В яких одиницях в системі СІ вимірюється тиск рідини?

3. Яку течію рідини вважають стаціонарною?

4. Які сили діють на тіло, що рухається у рідині чи газі ?

5. За рахунок чого виникає підйомна сила крила літака?

6. Запишіть рівняння нерозривності нестисливої рідини.

7. Запишіть рівняння Бернуллі та поясніть значення його складових.

8. Які режими течії речовини Ви знаєте?

9. Що визначає число Рейнольдса та від чого воно залежить?

10. Які методи експериментального вимірювання в’язкості рідини Ви знаєте? У чому полягає їх суть?

Г

68

ЛАВА 8.

РелятивістсьКа механіка

8.1. Перетворення Галілея. Механічний принцип відносності.

Розглянемо дві інерціальні системи відліку. Систему K (з координатами x, y, z), котру будемо вважати умовно нерухомою, та систему - K¹ (з координатами x¹, y¹, z¹), що рухається відносно системи К рівномірно та прямолінійно зі швидкістю U = const.

Тоді у довільний момент часу розташування цих систем буде мати вигляд, показаний на рис. 8.1. У цьому випадку положення довільної точки А в системі відліку K¹ визначається радіусом-вектором , а в системі відліку K - радіус-вектором .

Швидкість U має напрямок вздовж лінії 00¹, а значить радіус-вектор, проведений з точки 0 до точи 0¹, дорівнює: .

Використовуючи правило додавання векторів, маємо . Або:

(8.1)

де t, t¹ - час у відповідних системах відліку.

Система рівнянь (8.1) отримала назву перетворення координат за Галілеєм. Друге рівняння у цій системі відображає той факт, що в класичній механіці плин часу не залежить від руху системи відліку.

Візьмемо похідну від першого рівняння у системі (8.1) за часом та урахувавши, що така похідна від радіуса-вектора дорівнює швидкості, отримаємо класичний закон додавання швидкостей:

, (8.2)

де - швидкості точки А у системах відліку К та К¹ .

С

69

піввідношення (8.2) є наслідком не тільки векторного характеру швидкості, а й тих уявлень про час та простір, які лежать в основі класичної механіки.

Враховуючи, що U = const, похідна за часом від рівняння (8.2), буде дорівнювати:

(8.3)

Тобто прискорення точки А однакове у системах відліку K та K¹. Припускаючи, що маса цієї точки однакова у всіх системах відліку, маємо:

(8.4)

Таким чином, ми довели механічний принцип відносності: рівняння динаміки при переході від однієї системи відліку до іншої залишаються незмінними, тобто вони інваріантні відносно перетворень координат за Галілеєм.

Узагальнюючи механічний принцип відносності, можна стверджувати, що усі закони класичної механіки не змінюють свою форму при перетвореннях координат та часу за Галілеєм.

При доказі механічного принципу відносності ми зверталися до двох аксіом: про інваріантність проміжків часу між двома подіями та про інваріантність відстаней між двома точками по відношенню до вибору системи відліку.

З першої аксіоми випливає, що хід часу однаковий у всіх системах відліку, а з другої, - що розміри тіл не залежать від швидкості їх руху.