Класична механіка. . Глава 5. Динаміка обертального руху. .

41

, , (4.31)

де W₁ - кінетична енергія першого тіла до удару.

Аналізуючи вирази (4.31) неважко збагнути, що у випадку коли m₂ >> m₁ (наприклад, кування заліза молотом), маємо А_Д  W₁, тобто уся кінетична енергія молота витрачається на роботу деформування поковки.

А у випадку, коли m₁ >> m₂ (наприклад, забивання цвяхів молотком), маємо А_Д  0, тобто уся кінетична енергія від першого тіла передається другому і витрачається на його переміщення.

4.6. Контрольні завдання і запитання.

1. Як у загальному випадку визначається робота сили?

2. При яких умовах сила, що прикладена до тіла, не виконує роботи?

3. Чи залежить кінетична енергія тіла від вибору системи відліку?

4. Що таке потенціальна енергія?

5. Які сили є консервативними, а які - неконсервативними?

6. Наведіть формулу зв’язку консервативної сили з потенціальною енергією.

7. Чому дорівнює потенціальна енергія пружно деформованого тіла?

8. Що називається повною механічною енергією тіла?

9. Як формулюється закон збереження повної механічної енергії?

10. Сформулюйте визначення коефіцієнта відновлювання.

11. Дайте визначення абсолютно пружного та абсолютно непружного удару.

Г 42 лава 5. Динаміка обертального руху

5.1. Момент сили.

Рис. 5.1.

Моментом сили відносно точки О називається величина, яка дорівнює векторному добутку радіус-вектора , проведеного від точки О до точки прикладання сили , на цю саму силу:

, (5.1)

Вектор моменту сили нормальний до площини, де розташовані вектори та , і визначається за правилом векторного добутку (див рис. 5.1).

Розкриємо векторний добуток (5.1) і отримаємо модуль вектора моменту сили:

М = r F sin = r F sin(-) = F L ,

де L - плече сили F, тобто найкоротша відстань між лінією дії сили і точкою обертання,  - кут між векторами та .

Тіло, що має деяку точку обертання, буде знаходитись в рівновазі за умови, що сума моментів сил відносно цієї точки буде дорівнювати нулю:

, (5.2)

Одиниця виміру моменту сили в системі СІ: [М]=[FL] = [Н м].

5.2. Момент інерції. Теорема Штейнера.

Моментом інерції матеріальної точки відносно осі обертання називається скалярна величина, що дорівнює добутку маси m точки на квадрат її відстані r до осі обертання:

J = m r² , (5.3)

Розглянемо механічну систему, яка обертається з постійною кутовою швидкістю навколо осі Z (див. рис. 5.2).

М

43

оментом інерції J механічної системи відносно осі обертання Z (див. рис. 5.2) називають скалярну величину, що дорівнює сумі добутку мас усіх тіл, які входять в систему, на квадрат їх відстані до осі обертання і визначають з наступного рівняння:

Рис. 5.2.

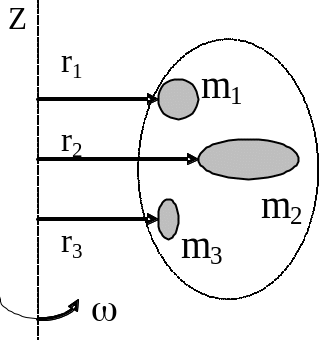
, (5.4)

У випадку неперервного розподілу маси тіла, сума (5.4) перетворюється на інтеграл такого вигляду:

, (5.5)

де V, m - об’єм та маса тіла, ρ – густина речовини, з якої зроблено тіло.

Обчислення інтегралу виду (5.5), як правило, є нелегким завданням, але для ряду геометричних фігур моменти інерції визначені.

Рис. 5.3.

Наведемо отримані результати для деяких з них.

Однорідний циліндр. Вісь Z проходить вздовж осі циліндра:

J_z = ¹/₂ mr² , (5.6)

Тонкий однорідний стрижень. Вісь Z перпендикулярна осі стрижня і проходить через його середину.

J_z = ¹/₁₂ mL² , (5.7)

Однорідна куля. Вісь Z проходить через центр кулі:

J_z = ²/₅ mr² , (5.8)

де m, r, L - маса, радіус та довжина відповідної фігури.

А тепер розглянемо тіло масою m, яке одночасно обертається навколо осі О¹, що проходить через його центр мас, та осі О, яка паралельна першій (див. рис. 5.3).

У

44

цьому випадку момент інерції тіла відносно осі обертання О може бути визначений за допомогою теореми Штейнера: момент інерції тіла J відносно довільній осі обертання дорівнює сумі моменту інерції J_С відносно осі, яка паралельна даній і проходить через центр мас тіла, та добутку маси тіла на квадрат відстані між осями:

, (5.9)

де m - маса тіла, d - відстань між осями.

Момент інерції тіла при обертальному русі - це аналог маси тіла при його прямолінійному русі.

Одиниця виміру моменту інерції в системі СІ така: [J] = [mr²] = [кг м²].