Класична механіка. . Глава 3. Сили в механіці. .

2 21 .6. Центр мас системи та закон його руху.

Центром мас (центром інерції) механічної системи називається уявна точка С, положення якої характеризує розподіл мас цієї системи. Центр мас задається за допомогою радіуса-вектора :

, (2.11)

де m_і - маса i-ої матеріальної точки у системі, - її радіус-вектор, m – загальна маса механічної системи.

Визначимо швидкість руху центру мас:

, (2.13)

Тобто . Підставивши цей вираз у формулу (2.6), одержимо рівняння руху центру мас механічної системи:

, (2.15)

де - вектор прискорення руху центра мас системи.

Таким чином, центр мас механічної системи рухається таким же чином, як і матеріальна точка, в якій зосереджена маса всієї системи і на яку діє сила, що дорівнює рівнодіючій усіх прикладених до системи сил.

2.7. Контрольні завдання і запитання.

1. В яких системах відліку виконуються закони Ньютона?

2. Сформулюйте усі три закони Ньютона.

3. Які сили називають внутрішніми, а які зовнішніми ?

4. Що називають імпульсом матеріальної точки?

5. Сформулюйте закон збереження імпульсу.

6. Сформулюйте принцип незалежності дії сил.

7. Наведіть рівняння руху центра мас системи матеріальних точок.

Г

22

ЛАВА 3.

СИЛИ В МЕХАНІЦІ

3.1 Деформування твердих тіл. Сила пружності.

Вище було дано поняття абсолютно твердого тіла, але у природі таких тіл не буває. Усі реальні тіла під дією сил змінюють свою форму та розміри, тобто деформуються. Якщо після закінчення дії сили тіло набуває початкових розмірів та форми, то таке тіло називають пружним, а таку деформацію пружною. Деформації які зберігаються у тілі після закінчення дії зовнішніх сил отримали, назву пластичних.

Усі види пружних деформацій можуть бути зведені до трьох видів: розтягнення, стискання та зсув (див. рис. 3.1).

Сила, діюча на одиницю площі поперечного перерізу S, отримала назву механічної напруги :

, (3.1)

Якщо сила спрямована по нормалі до поверхні, то напруга називається нормальною, а якщо по дотичній - тангенціальною.

Кількісною мірою, яка характеризує рівень деформації тіла, є його поперечні d та поздовжні L абсолютні деформації.

Відношення абсолютної деформації до початкового розміру зразка отримало назву: відносна поперечна _ та відносна повздовжня _ деформації, які визначаються з виразу (3.2).

Розтягнення Стискання Зсув

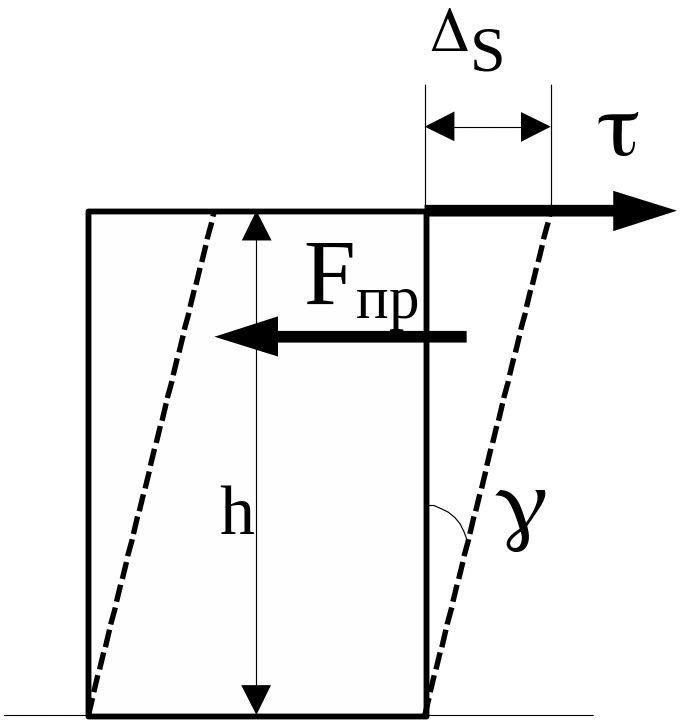
Рис. 3.1.



23

_ = L / L , _ = d / d , (3.2)

Відношення поперечної _ деформації до поздовжньої _ називається коефіцієнтом Пуасона :

Рис. 3.2.

 = - _ / _ , (3.3)

Теоретичні значення коефіцієнта Пуасона, за винятком гуми, знаходяться у межах: 0 <  < 0,5. Знак "-" у формулі (3.3) означає, що поперечна та поздовжня деформації завжди мають протилежний напрямок (див. рис. 3.1).

Згідно з законом Гука відносна деформація тіла прямо пропорційна прикладеній до нього механічній напрузі:

, (3.4)

де Е - модуль пружності (модуль Юнга).

З виразу (3.4) видно, що модуль Юнга за фізичним змістом є такою механічною напругою, яку необхідно прикласти до тіла, аби його відносна деформація стала рівною одиниці.

Внутрішні сили, що чинять опір зовнішнім силам при деформуванні твердих тіл, отримали назву пружних сил.

Відповідно до третього закону Ньютона пружна сила F_пр завжди рівна за модулем та протилежна за напрямком значенню зовнішньої сили F_зов:

F_пр = - F_зов , (3.5)

Сили пружності виникають в усьому об'ємі тіла, що деформується, і не залежать від його розмірів.

Використовуючи вирази 3.1, 3.2 та 3.4, визначимо значення пружної сили F_пр :

,

Тоді з урахуванням (3.5) отримаємо:

Рис. 3.3.

, (3.6)

де k = ES/L - коефіцієнт пружності твердого тіла , Н/м.

Коефіцієнт пружності суттєво залежить від геометричних розмірів тіла. Так, якщо довжину тіла зменшити у два рази, то його коефіцієнт пружності, згідно з виразом (3.6), збільшиться вдвічі.

Р

24

озглянемо більш детально деформацію зсуву (див. рис 3.1). Під дією тангенціальної напруги , прикладеної вздовж верхньої грані, тіло деформується на деякий кут зсуву .

Згідно з законом Гука кут зсуву прямо пропорційний тангенціальній напрузі, що викликала цей зсув:

, (3.7)

де G - модуль зсуву, Па.

З виразу (3.7) видно, що модуль зсуву за фізичним змістом являє собою таку тангенціальну напругу, при якій кут зсуву дорівнював одному радіану.

Чисельні значення параметрів Е і G визначаються експериментально. Деформації пружних тіл підпорядковуються закону Гука тільки до деякого значення, яке отримало назву межа міцності _мм. При механічній напрузі, що дорівнює межі міцності, наступає руйнування матеріалу (див. рис. 3.2).

У системі СІ механічна напруга, модулі пружності та зсуву вимірюються в паскалях: [, , Е, G] = [Н/м²] = [Па], кут зсуву - в радіанах [] = [рад.], абсолютна деформація - в метрах [L, d ] = [м], відносна деформація  це параметр без розміру.