6.1 Метод отсекающих плоскостей: постановка и общая схема решения, ме­тод Гомори для полностью целочисленных задач лп.

Метод отсекающих плоскостей (метод целочисленных форм)

Наиболее часто используемым методом для решения полностью целочисленных задач является метод Гомори.

Решение в данном методе сводится к решению последовательности специально построенных задач, каждая из которых получается из исходной путём добавления к её условиям дополнительного линейного ограничения (отсечения). При этом, k-м сечением будет линейное ограничение, которое вводится в задачу и отвечает следующим условиям:

- Любое целочисленное решение исходной задачи ему удовлетворяет

- Любое нецелочисленное решение исходной задачи ему не удовлетворяет

При этом, решение задачи на первом этапе, т.е. получение решения ослабленной задачи, это решение задачи ЛП.

Пусть задача ЛП решена обычным СМ и её решение не удовлетворяет условиям целочисленности, тогда составляется дополнительное ограничение, которое записывается в виде:

или эквивалентно : , где фигурные скобки означают дробную часть числа.

Для получения данных неравенств используется стандартная форма записи симплексной таблицы, которая предложена Таккером. Если её записать, то получим:

, где - целочисленная переменная, а все - текущие небазисные переменные, которые подчинены требованиям неотрицательности и целочисленности, а - соответствующие коэффициенты симплекс-таблицы.

Тогда уравнение отсекающей гиперплоскости, которое получается из предыдущего уравнения, имеет вид:

, где

S – это неотрицательная целочисленная переменная,

f_i – положительная дробная часть константы b_i,

f_ij – положительная дробная часть константы y_ij.

Т.е. можно записать:

, где - целая часть числа (это наибольшее целое число, не превосходящее ).

Поскольку на переменные не наложено условие неотрицательности, уравнение отсекающей гиперплоскости может быть выведено из любого уравнения, полученного в виде некоторой линейной комбинации уравнений симплекс-таблицы.

Границы сечения обычно устанавливаются из уравнения, в котором b_i не является целым числом, т.е. там, где f_i0, что обуславливает появление лишь одной порождённой задачи (метод Гомори всегда порождает только одну задачу). Для каждой последующей порождённой задачи, выбранной на шаге 2 (см. алгоритм), решение ослабленной задачи ЛП на шаге 3 путём «дооптимизации» её с использованием двойственного СМ.

Д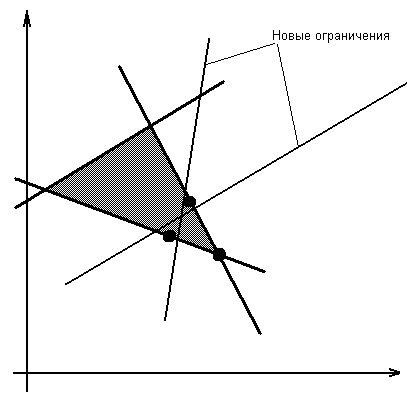 ля задач ЛП, включающих m ограничений и n переменных всегда существует оптимальное решение, содержащее не более m положительных переменных. Для задач ЦП такой же размерности может оказаться необходимым, чтобы все переменные были строго положительны. В силу этого требования, размерность исходной задачи может практически неограниченно увеличиваться, и возможность получения целочисленного решения недоказуема до самой последней итерации.

Сущность алгоритмов, основанных на методах отсечения, легко объяснить, если обратиться к геометрической интерпретации. В качестве выпуклой оболочки множества допустимых целочисленных решений представляется множество всех решений задачи, отвечающих требованиям целочисленности. При этом оптимальным решением является одна из экстремальных точек этого множества. Если найденная в результате решения экстремальная точка не удовлетворяет условию целочисленности, формируемым ограничением она отсекается, однако, соответствующая новому ограничению гиперплоскость не должна отсекать ни одного целочисленного решения.