§4. Касательная кривой. Теорема о касательной.
Пусть
– кривая,
– точка на ней и
– прямая, проходящая через точку
.
Возьмём на кривой точку
и обозначим её расстояние от точки
и прямой
через
и
соответственно.
Определение.
Прямая
называется касательной к
кривой
в точке
,
если
,
когда
.
Е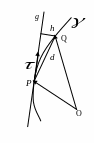
сли
кривая
в точке
имеет касательную, то прямая
при
сходится к этой касательной. Обратно,
если прямая
при
сходится к некоторой прямой
,
то эта прямая является касательной.
Для доказательства этого утверждения
достаточно заметить, что отношение
есть синус угла между прямыми
и
,
а он для достаточно малых углов может
быть заменён этим углом. Следовательно,
если при
отношение
,
то угол между прямыми
и
также стремится к нулю, то есть
сходится к касательной.
Теорема. Гладкая кривая без особых точек имеет в каждой точке касательную и притом единственную.
Если
векторное уравнение
кривой, то касательная в точке
,
соответствующей значению параметра
,
параллельна вектору
.
Доказательство. Пусть – гладкая параметризация кривой в окрестности точки , соответствующей значению параметра .
Доказательство теоремы проведем в два этапа:
1. Предполагая, что касательная в точке существует, докажем, что она параллельна вектору .
2. Докажем, что всякая прямая, проходящая через точку параллельно вектору , является касательной.
Итак,
допустим, что кривая
в точке
имеет касательную
и пусть
– единичный направляющий вектор
касательной
.
Расстояние
d
точки
,
соответствующей значению параметра
,
от точки
равно
.
Найдем
.
Это высота параллелограмма построенного
на векторах
и
,
проведенная к основанию
.
Следовательно,
равно площади S
параллелограмма, деленной на длину
основания
:
,
так как
.
По определению касательной
,
при
.
Но
,
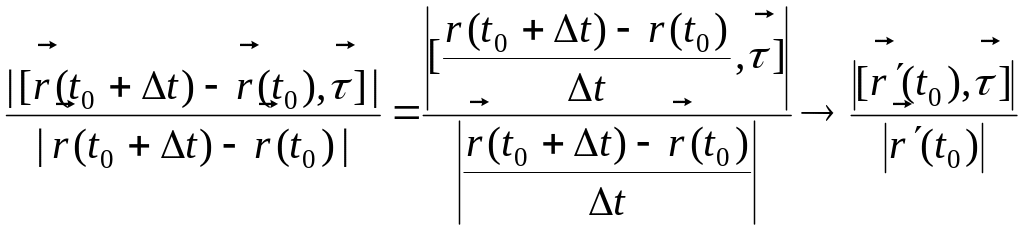при
.
Таким
образом, так как
,
то
.
А это возможно только тогда, когда вектор
имеет направление вектора
.
Следовательно, если касательная
существует, она параллельна вектору
и, так как он ненулевой, то единственна.
Докажем обратное. Пусть – произвольная прямая, проходящая через точку с направляющим вектором . Как показывают предыдущие выкладки, для прямой
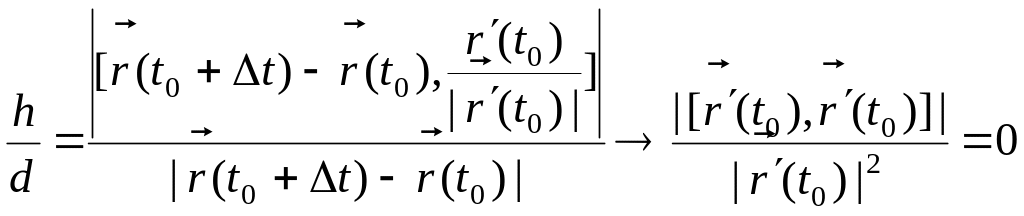при
.
Следовательно, прямая – касательная к кривой .
Теорема доказана полностью.
Зная направляющий вектор касательной, нетрудно составить её уравнение. Действительно, если кривая задана векторным уравнением , то векторное уравнение касательной можно записать так:
,
где
–
параметр.
Выведем уравнение касательной для различных случаев аналитического задания кривой .
1.
Пространственная кривая задана
параметрическими уравнениями
и точка
.
Тогда уравнения касательной к кривой
в точке P
имеют вид:
или
.
Если кривая плоская, уравнение ее касательной запишется так:
.
2.
Кривая
задана уравнениями
.
Тогда уравнения касательной примет вид
,
где
– координаты точки P.
В частности, если кривая плоская и задана
уравнением
,
то уравнение касательной к ней будет
.
3.
Составим уравнение касательной к кривой
,
заданной неявными уравнениями
в
точке
.
Пусть
– какая-нибудь регулярная параметризация
кривой в окрестности точки P.
Тогда имеем тождества
.
Дифференцируя
эти тождества по t,
получим систему двух однородных линейных
уравнений относительно трех неизвестных
,
:
,
.
Следовательно,
векторы
и
коллинеарные; здесь
={
},
{
},
{
}.
Отсюда
и уравнение касательной примет вид
,
где все производные вычислены в точке касания .
Если кривая плоская и задана уравнением , то уравнение касательной будет
.
Определение. Нормальной плоскостью кривой в точке P называется плоскость, проходящая через точку P перпендикулярно касательной в этой точке.
Составить уравнение этой плоскости после того, как известно уравнение касательной для любого случая аналитического задания кривой, не составляет особого труда и предлагается в качестве легкого упражнения.