1.2 Механические характеристики рабочих машин

Для понимания уравнения движения электропривода необходимо знать механическую характеристику двигателя ω = f (М) и зависимость момента рабочей машины от скорости.

Различают четыре вида механических характеристик рабочих машин, рис. 1:

1) Не зависящие от скорости механические характеристики (1)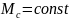 . Характерны для подъемных машин, поршневых компрессоров, механизмов передвижения. Мощность таких машин растет со скоростью.

2) Линейно - возрастающие характеристики 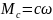(2). Такую характеристику имеет генератор постоянного тока. Здесь мощность пропорциональна квадрату скорости.

3) Нелинейно – возрастающие (параболические) механические характеристики (3). Такую характеристику имеют машины, преодолевающие сопротивление воздуха или жидкости (вентиляторы, насосы, центрифуги). Их мощность примерно пропорциональна кубу скорости.

4) Нелинейно – спадающие характеристики (4). Такие характеристики характерны для металлорежущих станков токарной группы, стругов, скребковых конвейеров. Мощность, потребляемая такими машинами, постоянна.

1.3 Приведение моментов сопротивления и инерции

Наиболее распространенной конструктивной формой большинства рабочих машин является сочленение с электродвигателем посредством редуктора. В этом случае скорости движения вала рабочей машины и вала двигателя различны и при использовании уравнения движения электропривода все моменты должны быть приведены к единой скорости или к единому валу – валу электродвигателя. При приведении необходимо учитывать потери в редукторе. Рассмотрим кинематическую схему, приведенную на рис.2. Двигатель сочленен с рабочей машиной через редуктор с передаточным отношением i. Требуемая мощность на валу рабочей машины равна:

.

Мощность на валу электродвигателя, учитывая потери в редукторе, составит:

.

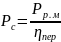Заменив мощность через момент 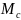и угловую скорость двигателя ω, получим: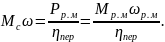

Решив уравнение относительно , получим:

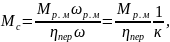
где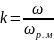 - передаточное число редуктора.

При работе электродвигателя в тормозном режиме КПД передачи следует записывать в числителе, так как поток энергии имеет обратное направление, т.е.: .

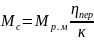Приведение моментов инерции, как правило, к валу электродвигателя основано на том, что величина суммарного запаса кинетической энергии, отнесенная к валу двигателя, постоянна. Кинетическая энергия:

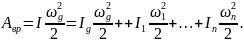
После преобразования этого уравнения получим момент, приведенный к валу двигателя :

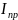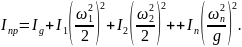
В механизмах имеющих вращательно и линейно – движущиеся части (носовые лебедки драг) для получения суммарного момента на валу электродвигателя нужно инерционные силы поступательного движения и силы сопротивления поступательному движению привести к вращательному движению, рис.3.

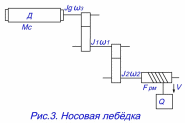
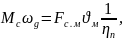
где 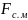- сила сопротивления механизма поступательному движению, отсюда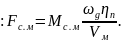

Приведение поступательно движущихся масс осуществляется на основе равенства закона кинетической энергии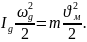

Отсюда 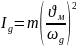при обратном приведении .

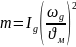1.4 Понятие о кинематике электропривода.

Основные кинематические величины, характеризующие поступательное движение: скорость - , путь – x, ускорение – α, связанные между собой уравнениями: , .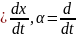

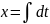Для вращательного движения основные величины: ω – скорость,  – путь,  – ускорение, .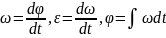

Для машин с частыми пусками большую роль играет ускорение. Чем ε больше, тем выше Q, но с ростом ε возрастают нагрузки на элементы машины, канаты, редукторы, что повышает требования к их прочности. Ускорение подъемных машин ограничивается физиологическими способностями людей.

Представление о законе движения электропривода дает диаграмма скорости.