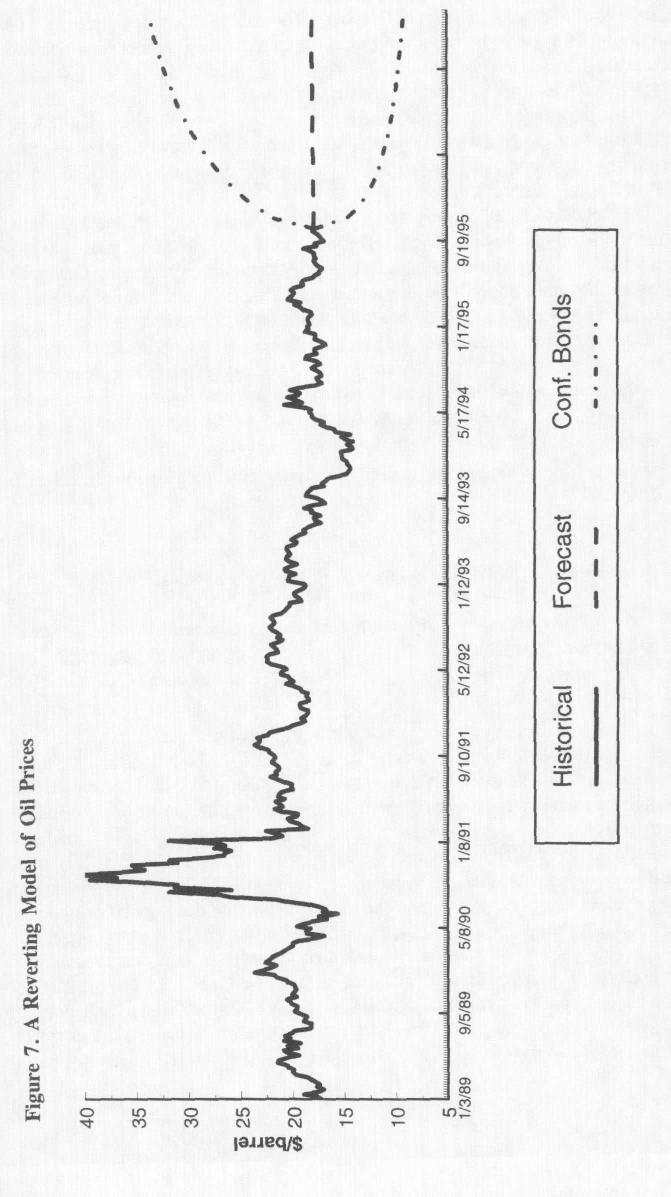
Оценка параметров модели на основе фактических ценовых данных

В работе Schwartz (1997) один из вариантов данной модели был использован для оценки параметров динамики цен на золото, нефть и медь. Обнаружено, что параметры модели невозможно подогнать под фактическую динамику цен на золото, имевшую место в период с 1985 по 1995 гг, что свидетельствует об отсутствии в ней тенденции возврата к среднему. Среди биржевых товаров золото больше всех остальных похоже на чистый финансовый актив, для которого должна выполняться модель случайного блуждания и для которого теоретические предпосылки наличия тенденции возврата к среднему наиболее слабы. Так что полученный результат не должен вызывать удивления. Исполь­зуя фактические данные цен на нефть за период с января 1985 г. по февраль 1995 г. и задав  = 0, Шварц (Schwartz, 1997) получил оценки коэффициента возврата к среднему  в интервале от  = 0,3 до 0,7, а волатильности – от  = 26% до 33%. На основе данных о ценах на медь за период с июля 1988 г. по февраль 1995 г. и заданного значения параметра сдвига  = 0 автор получил оценку коэффициента возврата к среднему  = 0,4 и волатильности  = 23%

Интерпретация фактических ценовых данных на основе альтернативных моделей ценовой динамики

Именно выбор аналитиком модели стохастической ценовой динамики определяет его интерпретацию фактических данных о движении цены на товар в прошлом. Например, в описанном выше случае цен на нефтяь безусловная оценка параметра сдвига, полученная для модели случайного блуждания, равнялась , а для модели возврата к сред­нему – уже . Различие в оценках вытекает из того простого факта, что различ­ные модели подразумевают неодинаковые гипотезы о любом отдельно взятом изменении цены. Не углубляясь в теоретические детали, просто напомним, что модель случайного блуждания разлагает каждое приращение цены на две компоненты, в то время как модель возврата к среднему разлагает то же самое изменение цены уже на три составляющие. Оценки параметров сдвига и волатильности, полученные для этих двух моделей, просто не могут быть одинаковыми, хотя обе компоненты присутствуют и в той, и в другой модели. Конечно, это наше рассуждение является сильным упрощением и в серьёзном анализе может рассматриваться лишь как отправная точка. Объяснить, как и почему различаются оценки параметров, полученные для двух моделей ценовой неопреде­лённости, поможет природа двух вариантов разложения ценовых изменений на компоненты.

В модели случайного блуждания предполагается, что, например, суточные изменения цены, наблюдаемые в течение двух последовательных дней, имеют идентичную струк­туру, состоящую частью из общего тренда, описываемого параметром сдвига, а частью – из случайного элемента. Следовательно, изменение цены в любой день рассматривается как одинаково чистое наблюдение общего тренда. Если в один из дней наблюдается масштабное падение цены, а в другой – её скромный подъём, то аналитик, применяющий модель случайного блуждания, оценит среднее изменение цены небольшой отрицательной величиной. С другой стороны, однофакторная модель возврата к среднему предполагает, что некоторая доля ежедневных изменений цены объясняется тенденцией возврата к долгосрочному тренду. Прежде чем оценивать параметр сдвига, применяющий данную модель аналитик должен избавиться от этой доли ежедневных ценовых изменений. Если подъём цены на второй день частично рассматривать как возврат к долгосрочному тренду, а почти всё падение в течение первого дня относить к долгосрочной стационарной тенденции, то аналитик, пользующийся моделью возврата к среднему, может в итоге оценить параметр сдвига весьма значительной отрицательной величиной.

То же самое различие в интерпретации исходных данных влияет и на оценку ценовой волатильности. Аналитик, использующий модель случайного блуждания, считает некото­рую долю ежедневного изменения цены результатом действия параметра сдвига, а остаток – независимым наблюдением среднего ежедневного отклонения цены или средней вола­тильности. Аналитик, использующий модель возврата к среднему, также объясняет часть ежедневного изменения цены действием параметра сдвига, но оценивает он этот параметр иной величиной. Другую часть ежедневного изменения цен аналитик объясняет тенден­цией возврата к долгосрочному равновесному значению. Только после исключения влия­ния этих двух факторов аналитик переходит к оценке величины суточной волатильности, исходя из остаточной «необъяснённой» доли при­ращения цены в рассматриваемый день. Две модели дают две различные численные оценки параметра суточной волатильности, во-первых, потому, что не совпадают оценки параметра сдвига, а, во-вторых, потому, что в одной из моделей предполагается наличие тенденции возврата к долгосрочной стационарной траектории.

Тенденция возврата к среднему также может служить вероятным объяснением того отмеченного выше факта, что оценка параметра волатильности в модели случайного блуждания чувствительна к длительности интервала времени, за который измеряется изменение цены. Если тенденция возврата к среднему действительно имеет место, то вариация цены при её ежемесячном измерении должна в общем случае быть меньше вариации цены при ежедневном учёте изменений, так как некоторая доля суточного приращения цены взаимопогашается в течение месяца из-за стремления цены вернуться на долгосрочную стабильную траекторию. Численная оценка параметров модели возврата к среднему представляет собой более сложную задачу, чем оценка параметров модели случайного блуждания. Подробное обсуждение данного вопроса можно найти в работах Lo and Wang (1995) и Campbell, Lo and MacKinley (1997).

Figure 7.