Однофакторная модель возврата к среднему при описании товарных цен.

Модель, заданная уравнением (4), – это вариант модели экспоненциального угасания, представленной в статье Laughton and Jacoby (1993). В сопутствующих статьях Salahor (1998) и Bradley (1998) эта же модель называется «моделью возврата цены к среднему». В работе Laughton and Jacoby (1993) показана эквивалентность этих двух интерпретаций модели, в первой из которых используются прогнозные значения цены (см. Salahor (1998) и Bradley (1998)), а в другой – сама цена (как у нас). Разновидность данной модели применена в работах Ross (1995) и Schwartz (1997)⁶. Поскольку в уравнении (4) имеется лишь одна случайная переменная, dz, постольку данная модель возврата к среднему называется однофакторной.

На Рис.6 показаны две сымитированные траектории данного однофакторного процесса возврата к среднему при значениях параметров  = 3% и = 20% (как в приведённых выше имитациях случайного блуждания), а также  = 2 и . Тонкой пунктирной линией намечена равновесная траектория роста долгосрочной цены с темпом 3% в год, заданная уравнением . Эта тот стабильный тренд, к которому стремится вернуться цена. В случае первой имитации («образец А») цена в конце двухлетнего периода принимает значение Р₂ = 104, что немного ниже долгосрочного равновесного значения , и потому следует ожидать, что далее цена некоторое время будет расти с темпом, превышающим 3% годовых, пока не вернётся на долгосрочную равновесную траекторию. Этот предсказанный путь цены показан тонкой сплошной линией, исходящей из точки с координатой t = 2. Сверху и снизу данной прогнозной траектории двумя пунктирными кривыми намечены границы прогнозного доверительного интервала. В противоположность процессу случайного блуждания, ширина доверитель­ного интервала быстро достигает некоторого предела, оставаясь затем приблизительно постоянной.

В случае второй имитации («образец В») цена в конце двухлетнего периода принимает значение Р₂ = 123, что значительно превышает долгосрочного равновесного значения . Поэтому далее ожидается, что вначале цена будет падать, пока не приблизится к долгосрочной равновесной траектории и не возобновит рост с темпом 3% годовых. Обратите внимание на то, что прогнозное значение цены, следующей процессу возврата к среднему, всегда расположено неподалёку от долгосрочной траектории, вне зависимости от изменений цены в прошлом, в то время как при случайном блуждании прогноз цены постоянно сдвигается вверх и вниз, следуя за происходящими в действи­тельности ценовыми скачками. Именно поэтому случайное блуждание является нестаци­онарным процессом, а однофакторная модель возврата к среднему – стационарным.

Имитация траекторий стохастической ценовой динамики

На рис.7 показана фактическая динамика цен на нефть, уже изображённая на Рис.1, но теперь на неё наложен прогноз цен, основанный на модели возврата к среднему. Оценка параметра сдвига, вытекающая из этой модели, равна . Однако, ради того, чтобы прогнозные значения и прочие детали анализа оставались сравнимыми с построен­ными выше для модели случайного блуждания (см. Рис.1), мы задали значение параметра сдвига равным , как в модели случайного блуждания. В этом случае оценка волатильности получилась равной , а оценка долгосрочной равновесной цены – равной . Сплошной линией на графике показана траектория прогнозной дина­мики цены, начинающаяся со значения 17,84 долл/барр в октябре 1995 г. и затем немного возрастающая до равновесного значения 18,86 долл/барр. Это не похоже на модель случайного блуждания, где прогнозная траектория цены остаётся горизонтальной на уровне цены октября 1995 г., равной 17,84 долл/барр. Несмотря на тот факт, что в обоих случаях использовалось одно и то же значение параметра сдвига, предсказанные траекто­рии движения цены различны. Следует также заметить, что доверительные границы будущих значений цены для модели возврата к среднему гораздо уже, хотя оценённое значение параметра волатильности практически идентично тому, что использовалось в модели случайного блуждания.

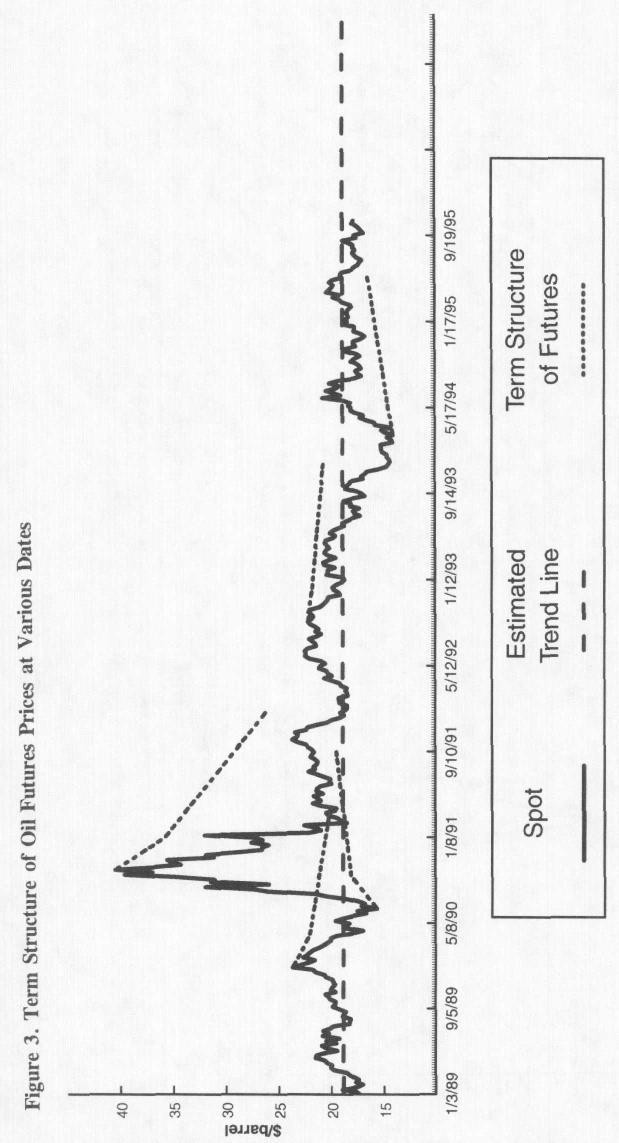
Рисунок 3. Структура цен на нефтяные фьючерсные контракты по срокам их исполнения на различные исходные моменты времени.

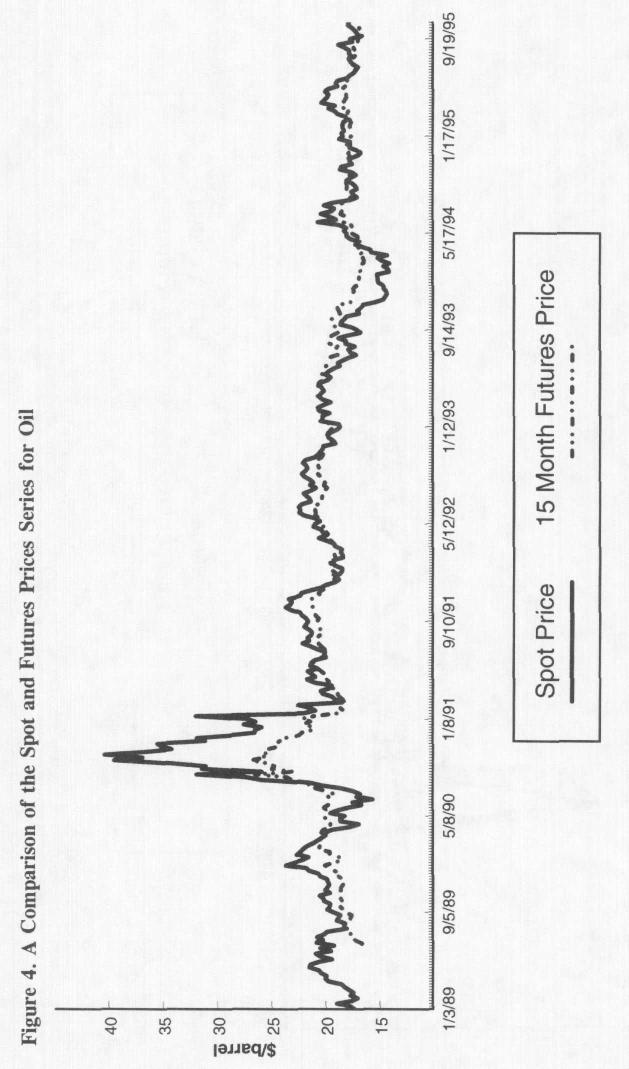
Рисунок 4. Сравнение временных рядов фьючерсных и спотовых цен на нефть.

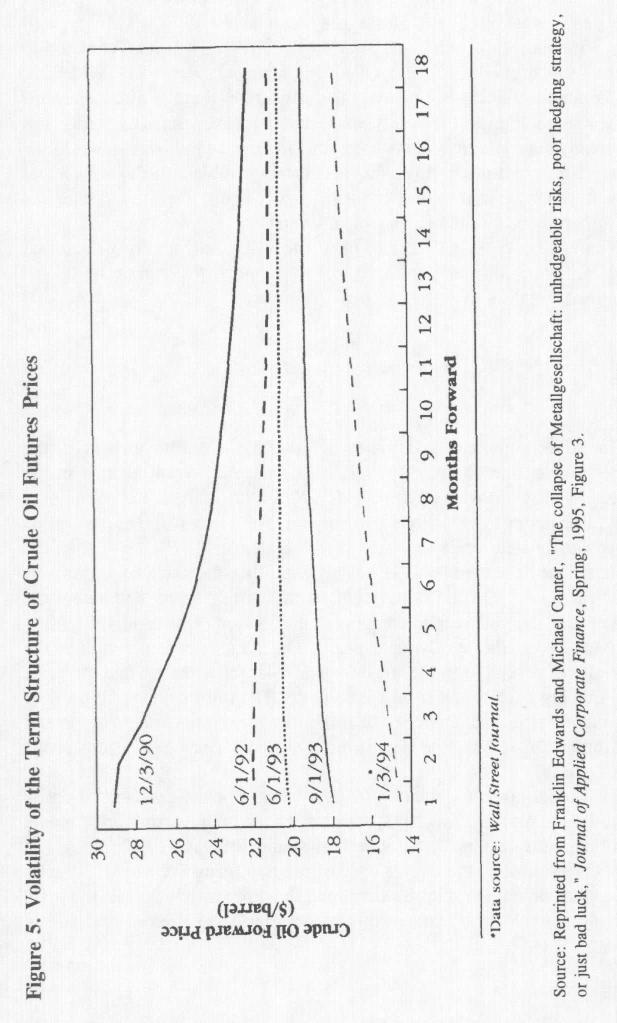
Рисунок 5. Волатильность структуры цен на фьючерсные контракты на сырую нефть в зависимости от сроков их исполнения.

Рис. 6. Модель возврата к среднему. Случайная реализация ценовой траектории, линия прогноза и доверительные интервалы. Тёмной сплошной линией показана фактическая динамика цены на товар в течение 2 лет. Тонкая пунктирная линия слева задаёт долгосрочную равновесную траекторию значений цены, исходящую из начального значения в $100 и растущую с темпом 3% годовых. Более жирная пунктирная линия справа представляет собой траекторию прогнозных значений цены на момент времени t = 2. Она берёт своё начало из фактического значения цены в этот момент, а затем приближается к долгосрочной равновесной траектории. Сложным пунктиром показаны границы 66%-го доверительного интервала для прогнозных значений цены на момент времени t = 2. Обратите внимание, что ширина доверительного интервала ограничена и с течением времени стремится к постоянной величине. Также обратите внимание на то, что лишь краткосрочный прогноз цены всё время пересматривается вслед за сдвигами значений текущей цены. В долгосрочной перспективе прогноз всегда приближается к долгосрочному равновесному значению цены.

Тёмной сплошной линией показана фактическая динамика цены на товар в течение 2 лет. Тонкая пунктирная линия слева задаёт долгосрочную равновесную траекторию значений цены, исходящую из начального значения в $100 и растущую с темпом 3% годовых. Более жирная пунктирная линия справа представляет собой траекторию прогнозных значений цены на момент времени t = 2. Она берёт своё начало из фактического на этот момент значения цены, а затем приближается к долгосрочной равновесной траектории. Сложным пунктиром показаны границы 66%-го доверительного интервала для прогнозных значений цены на момент времени t = 2. Обратите внимание, что ширина доверительного интервала ограничена и с течением времени стремится к постоянной величине. Также обратите внимание на то, что сдвиги значений текущей цены влияют лишь на краткосрочный прогноз цены. В долгосрочной перспективе прогноз всегда приближается к долгосрочной равновесной траектории цены.