Цены на фьючерсы и двухфакторная модель возврата к среднему

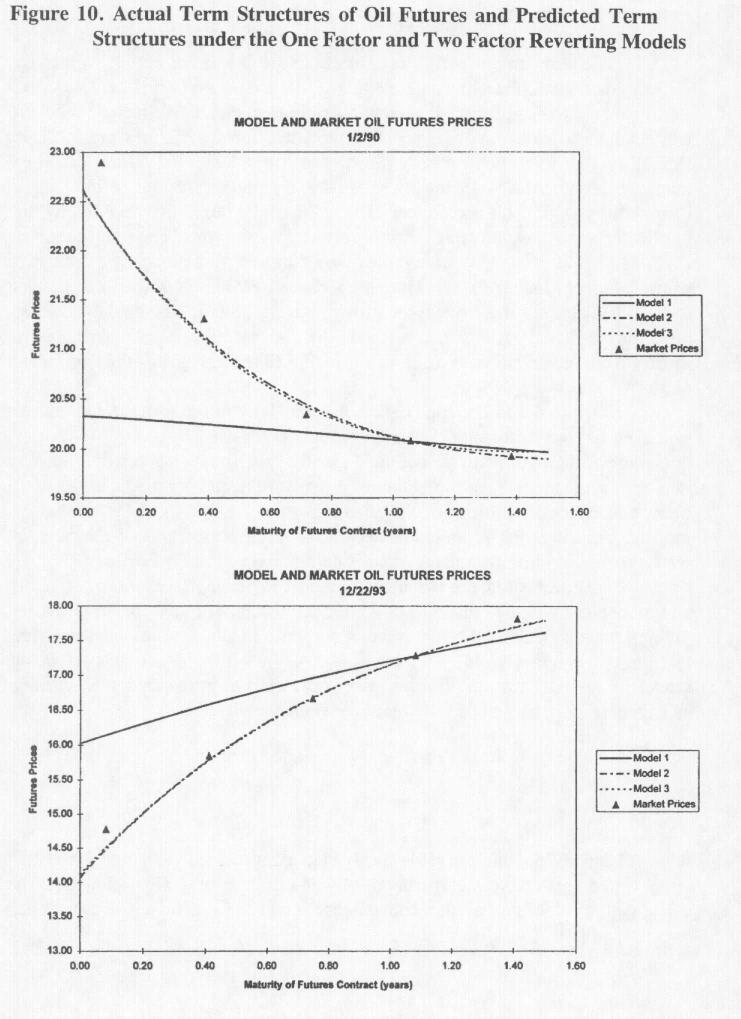
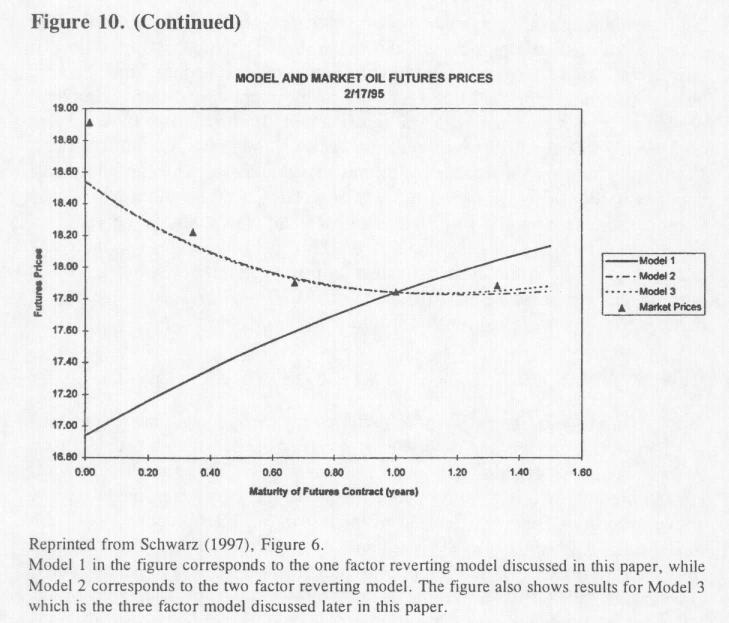
Срочная структура цен на фьючерсы в случае двухфакторной модели задаётся гораздо более сложным выражением, чем уравнение (10), оно приведено в Приложении. Поскольку двухфакторная модель гибче любой из однофакторных моделей, постольку и выбор возможных разновидностей срочной структуры фьючерсных цен, которые она способна сгенерировать, гораздо шире. По всей видимости, без этой гибкости невозможно добиться соответствия модели фактическим временным рядам ценовых данных о фьючерсных контрактах на многие товары. В работе Schwartz (1997) приводятся результаты для трёх товаров – золота, нефти и меди. Ценность гибкости, обеспечиваемой двухфакторной моделью, проиллюстрирована результатами, полученными для нефти, которые воспроизведены на Рис.10. Параметры как одно- , так и двухфакторной моделей возврата к среднему оценены на основе данных запериод с января 1990 по февраль 1995 г. Один из трёх графиков показывает действительную срочную структуру цен на фьючерсы, преобладающие на соответствующую дату, а другие – структуру, предсказанную каждой из двух моделей. Численные результаты наглядно иллюстрируют неполноценность однофакторной модели в сравнении с двухфакторной.

Несмотря на устрашающе сложный вид формулы цен на фьючерсы из двухфакторной модели, в её основе лежит базовый принцип. Точно так же, как динамика спотовой цены в двухфакторной модели представляет собой смесь динамик спотовой цены двух однофакторных моделей, срочная структура фьючерсных цен в двухфакторной модели является простой комбинацией срочных структур фьючерсных цен обеих однофакторных моделей. Процесс возврата к среднему является определяющим в краткосрочной перспективе, а процесс случайного блуждания, задающий стационарную траекторию, – в долгосрочной:

.

(11)

Здесь ^* обозначает ненаблюдаемый стационарный выигрыш от удобства обладания товаром, а равенство является приблизительным по причине наложения на процесс случайного блуждания процесса возврата к среднему. Операционно величина ^* рассчитывается, путём рассмотрения выигрыша от удобства обладания товаром в отдалённом временном горизонте, т.е. в пределе

lim_T→∞ (T),

где

(T) = (1/dt) ln [F_t(T + dt)/F_t(T)]

Это означает, что имеется возможность построить на основе долгосрочных фьючерсных контрактов оценочный ряд стационарных цен. Применяя равенство из уравнения (10) и подставляя в него полученную оценку стационарного выигрыша от удобства владения, получаем: . Поскольку стационарная цена сама представляет собой простой процесс случайного блуждания, этот ряд затем может быть использован напрямую для оценки параметра _P*. В работе Gibson and Schwartz (1991) эта процедура была применена по отношению к данным, покрывающим период с ноября 1986 г. по ноябрь 1988 г., и было определено, что волатильность стационарной цены на нефть, _P*, равна лишь 26%, в то время как значение волатильности спотовой цены на нефть, _P, лежит между 30% и 33%. Этот метод оценивания не полностью использует информацию, которая может быть выведена из всей срочной структуры фьючерсных цен, но он относительно прост, и в этом его преимущество. И хотя эта методика и не даёт нам оценок остальных ключевых параметров двухфакторной модели, мы можем извлечь большую пользу хотя бы из полученных оценок, так как денежная ценность долговременных активов в нефтяной отрасли часто больше зависит от долгосрочной динамики цены на нефть, чем от краткосрочной.

Это означает, что динамика стационарного процесса проявляется всё лучше и лучше в динамике цен на фьючерсные контракты при переходе к контрактам со всё более длительным сроком исполнения. В модели случайного блуждания цена фьючерса является простой функцией текущей цены и выигрыша от удобства владения. Аналогичная зависимость сохраняется и в двухфакторной модели. В долгосрочной перспективе цена фьючерса определяется прежде всего текущим значением стационарной цены и стационарным значением выигрыша от удобства владения товаром.

Хотя цены фьючерсов действительно снабжают нас важной информацией о динамике цен на товар и о стоимостной оценке связанных с этим товаром капитальных вложений, следует сделать одно предостережение. Публикуемые данные о ценах на фьючерсы редко можно найти для временных горизонтов, превышающих один год, и с долгосрочной стоимостной оценкой связано множество важных проблем. Динамика цен на фьючерсы с короткими сроками исполнения может существенно отличаться от динамики цен долгосрочных фьючерсных контрактов. Когда исследователь использует данные о краткосрочных фьючерсах для стоимостной оценки долгосрочных активов, вероятность ошибки становится весьма существенной. Упомянутая выше работа Gibson and Schwartz (1990) содержит великолепный разбор конкретного случая стоимостной оценки долго­срочных активов, имеющих отношение к нефти, с использованием данных рынка кратко­срочных фьючерсных контрактов, причём внимание уделено и вопросу о предполагаемых оценочных ошибках. В работе Schwartz (1997) также приводится информация о некоторых трудностях оценки долгосрочных активов с использованием значений параметров, оценённых на основе ценовых данных краткосрочного рынка фьючерсов.

Рисунок 10. Фактическая срочная структура цен на нефтяные фьючерсы и структурыа, предсказанные на основе одно- и двухфакторной моделей возврата к среднему.

Рисунок 10. (Продолжение).