4.4. Анализ методом динамического программирования

В соответствии с общей методологией динамического программирования, мы начинаем анализ с момента времени, которым заканчивается горизонт принятия решений, а затем движемся в направлении, противоположном потоку времени.

Если геологоразведочные работы завершаются успехом, то каждый проект перехо­дит к своей последней стадии – разработке, – которая начинается вместе с началом разработки участка недр и заканчивается ликвидационными работами. При анализе этой стадии мы должны определить политику завершения проекта, а также дать денежную оценку объекта разработки в каждом узле графа на момент начала разра­ботки. Оказывается, что все интересующие нас варианты стратегии прекращения добычи и начала ликвидационных работ можно параметризовать с помощью своего собственного ряда граничных условий для каждого размера запасов, где каждый ряд содержит граничное условие для каждого момента времени после начала разработки месторождения. Заданная таким образом стратегия состоит в том, что в каждый отдельно взятый момент времени, при условии, что действительная цена на нефть превышает соответствующее граничное значение, менеджеру следует продолжать добычу (если она уже не прекращена). В противном случае добычу следует прекратить и начать ликвидационные работы.

Следующая стадия проекта, которую необходимо рассмотреть – это стадия, предваряющая разработку, когда менеджер обладает гибкостью в принятии решения по поводу начала разработки. Стратегии поведения менеджера здесь можно параметризовать единственным пороговым значением цены для каждого размера запасов. При ценах, не превышающих этого порога, менеджеру следует отложить разработку на будущее. Если же цена превышает данное пороговое значение, то следует немедленно приступать к разработке.

Управленческие решения по поводу оконтуривания и геологоразведки также харак­теризуются каждое отдельным пороговым значением цены, разделяющим область низких цен, где наилучшей альтернативой является ожидание, и область высоких цен, где следует сразу же начинать работы (по оконтуриванию либо по геолого­разведке, в зависимости от ситуации).

Ниже приведено длинное и подробное структурное описание приёмов динамиче­ского программирования, использованных для воплощения в жизнь этого аналити­ческого плана. Некоторым читателям будет лучше пропустить этот материал во время первого чтения статьи и сразу перейти к Разделу 4.5, где описываются и обсуждаются полученные в итоге стоимостные оценки проекта и оптимальные пороговые значения цены на нефть.

4.4.1. Стадия разработки

Прежде чем начать, необходимо сделать три замечания. Во-первых, анализ стадии разработки будет зависеть от величины запасов, выявленной на стадии оконтури­вания участка недр. Однако, в течение стадии разработки начальная величина запасов не меняется, так что мы способны вести параллельные расчёты на этой стадии для каждого из интересующих нас размера запасов. Поскольку вероят­ностное распределение размера запасов является дискретным, постольку число параллельных расчётов, которые нам предстоит выполнить, конечное (четыре, если неопределённость запасов имеет место, и один – если нет). В последующей дискуссии мы будем рассматривать лишь один из подобных параллельных расчётов, так что размер запасов больше не нужно принимать во внимание.

Во-вторых, для стадии разработки мы сделаем упрощающее предположение, будто бы все управленческие решения принимаются, а денежные затраты и поступления совершаются в течение интервалов фиксированной длительности в один год. Это вполне соответствует практике проектного анализа, принятой сегодня в отрасли. Если кому-то такая аппроксимация кажется недостаточно тонкой, он может выбрать интервалы покороче.

В-третьих, несмотря на то, что, в принципе, добыча может продолжаться бесконеч­но, приемлемым приближением будет задать срок обязательного прекращения проекта (если оно ещё не произошло до этого), отнеся его далеко в будущее на стадии разработки проекта. Такое приближение не сильно разойдётся с действитель­ностью по причине дисконтирования времени, а также, что более важно, по причине высоких и растущих издержек добычи в отдалённом будущем, как показано на Рис.2. Из-за дисконтирования добыча в отдалённом будущем почти не отражается на общей стоимостной оценке проекта, а ввиду высоких издержек вероятность добычи в отдалённом будущем невелика.

Таким образом, мы начинаем наш анализ с некоторого отнесённого в далёкое будущее момента времени после начала разработки участка недр (ради того, чтобы получился конкретный пример, примем этот срок равным 50 годам). Будем считать, что в этот момент времени в любом случае придётся прекратить добычу и ликвидировать проект (если это ещё не было сделано). В нашем примере денежная оценка месторождения в этом состоянии отражает ликвидационные расходы и равна –36 млн долл.

Так как мы перешли к дискретному описанию времени, сделаем шаг в обратном направлении от года t = 50 к году t = 49. В каждом состоянии, соответствующем этому году, менеджер проекта обязан выбрать между прекращением и продолже­нием добычи. Если добыча прекращается, менеджер получает –36 млн долл. Если добыча продолжается, менеджер получает денежный поток, соответствующий до­быче, а также ценность будущих денежных потоков по проекту.

В году t = 49 стоимость будущих потоков денежных средств по проекту можно определить, рассчитав стоимость прав на ту ценность, которую будет иметь проект в году t = 50. В году t = 50 ценность проекта составит безрисковую отрицательную величину, равную –36 млн долл., так что стоимость прав на эту ценность в любом узле графа, относящемся к году t = 49, равна этой самой величине в –36 млн долл., дисконтированной на один год по безрисковой ставке в 3% годовых.

Чистый денежный поток года t = 49 будет зависить от объёма добычи, от значения цены на нефть и от издержек добычи. Объём добычи и величина издержек, в свою очередь, зависят от начального размера запасов нефти в месторождении. Мы уже задали размер запасов, так что каждый рассматриваемый узел графа нам следует обозначить каким-либо значением цены в году t = 49. Затем мы сможем получить денежную оценку месторождения, на котором ведётся добыча, зависящую от выб­ранного значения цены.

Цена на нефть представляет собой непрерывную неотрицательную переменную с неопределённой верхней границей. Однако, мы вынуждены работать с конечной сеткой ценовых значений, так как способны выполнить лишь конечное число вычислений. Очень высоким значениям цены соответствуют очень низкие значения вероятности их реализации. Благодаря этому условию вклад тех сценариев, в кото­рые вовлечены слишком высокие значения цен, в наш анализ невелик, и это позво­ляет нам заменить неопределённо высокую верхнюю границу очень высоким, но всё же конечным пороговым значением. Мы рассматриваем некоторое дискрет­ное число состояний, помеченных возможными значениями цен в соответствии с сеткой значений внутри заданного конечного разброса цен.

В каждом из этих состояний мы сравниваем два альтернативных решения – прекращение добычи либо продолжение добычи. Мы выбираем то из них, которое имеет более высокую ценность, и задаём денежную оценку проекта в заданном узле графа равной ценности этой альтернативы.

Далее, мы делаем ещё один шаг назад и оказываемся в году t = 48, где перед мене­джером опять стоит тот же выбор – прекратить осуществление проекта или про­должить добычу. В каждом из возможных в году t = 48 состояний (т.е. узлов графа) мы повторяем тот же самый анализ. Однако, теперь расчёт ценности будущих денежных потоков несколько усложняется. Вспомним, что ценность проекта в году t = 49 зависит от значения цены в году t = 49. Рассматриваемая из года t = 48 цена на нефть в году t = 49 представляет собой случайную величину. Поэтому в каждом состоянии в году t = 48 мы осуществляем однолетнюю оценку проектной ценности года t = 49, используя метод «цен состояний». Структура «цен состояний» в году t = 48 одинакова для всех состояний, характеризующихся одним и тем же значением цены на нефть. Следовательно, для каждого значения цены в году t = 48 мы можем рассчитать условное скорректированное на риск математическое ожидание стои­мости проекта в году t = 49, а затем дисконтировать его на один год.

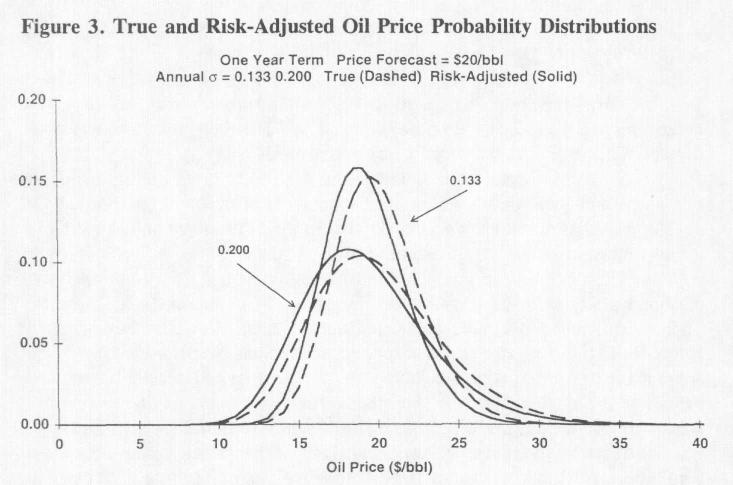
Для расчёта этого ожидаемого значения необходимо знать условное скорректиро­ванное на риск вероятностное распределение цены в году t = 49. В случае использу­емой нами модели ценовой неопределённости это распределение имеет логнормаль­ный вид. В Приложении В к первой статье детально описываются формулы, необ­ходимые для расчёта условных ожидаемых значений цен на нефть и ассоцииро­ванной дисперсии скорректированного на риск вероятностного распределения. На Рис. 3 показаны графики плотности вероятности действительных и скорректирован­ных на риск однолетних вероятностных распределений цены на нефть для рассмат­риваемых нами двух моделей ценовой неопределённости при заданном действитель­ном ожидаемом через один год значении цены, равном 20 долл/барр. Заметим ещё раз, что дисконтирование на риск означает левосторонний сдвиг скорректирован­ного на риск вероятностного распределения цены по сравнению с её действитель­ным распределением.

Располагая скорректированным на риск вероятностным распределением и сеткой значений стоимостной оценки проекта для года t = 49, мы можем применить метод численного суммирования (иначе называемого численным интегрированием) и найти соответствующее скорректированное на риск ожидаемое значение. Сущест­вует множество методов численного интегрирования. В данном случае мы приме­нили численное решение эквивалента известного дифференциального уравнения Блэка-Шоулза-Мертона, составленного для стоимостной оценки проекта в терминах времени и цены на нефть, а в качестве граничного условия использовали ценность проекта в году t = 49. Этот метод прямо подразумевает репликационный процесс в непрерывном времени. Важными чертами этого подхода являются его относитель­ная простота и скорость. Эти преимущества никак не зависят от того, как соотно­сятся данный математический метод и подразумеваемые экономические процессы. Детали (включая и другие граничные условия) приведены в Приложении А.

Эту расчётную процедуру следует повторять, отступая раз за разом на один год, вплоть до момента начала разработки. В результате мы получим денежную оценку проекта на этот момент времени как функцию от текущего значения цены на нефть (и величины запасов). Назовём эту оценку «ценностью проекта на момент начала разработки» – development value). Описанный процесс итеративных вычислений также задаёт, для каждого момента времени на стадии разработки, множество значений цены, при которых следует прекратить осуществление проекта (если к этому моменту проект ещё не был прекращён). Можно показать, что каждое из этих множеств формирует для соответствующего момента времени интервал ниже критического значения цены, называемый «границей оставления проекта» (abandonment boundary). Если реализованное в действительности значение цены оказывается ниже «границы оставления проекта», то менеджеру, претендующему на оптимальное исполнение своей роли с точки зрения гибкого принятия решений, следует закончить разработку и приступить к ликвидационным работам (если проект не был прекращен до этого). Если реализованное в действительности значение цены превышает «границу оставления проекта», то разработку месторож­дения или добычу следует продолжить.