Тема 6. Термодинамический цикл Ренкина

Реферативное изложение темы

Обратимый цикл Ренкина, как некое приближение цикла Карно к реальному воплощению. Сравнение термического КПД циклов Карно и Ренкина в идеальном и реальном вариантах. Объяснение интересного вывода: КПД реального цикла Ренкина выше КПД «реального» цикла Карно. Распространенность цикла Ренкина в реальных ТЭУ, в том числе и в ядерных (ЯЭУ).

Перечисленные выше недостатки, присущие паросиловой (паротурбинной) установке, в которой попытались бы осуществить цикл Карно на влажном паре, могут быть частично устранены, если отвод тепла от влажного пара в конденсаторе производить до тех пор, пока весь пар полностью не сконденсируется. В этом случае сжатию от давления Р₂ до давления Р₁ подлежит не влажный пар малой плотности, а вода (жидкость в общем случае какого-то другого рабочего тела). По сравнению с удельным объемом влажного пара в точке «d», удельный объем воды в точке « » весьма мал рис. 6.1, а ее сжимаемость пренебрежимо мала по сравнению со сжимаемостью влажного пара. Для сжатия воды (жидкости) и перемещения ее из конденсатора в нагреватель (котел, парогенератор, реактор) применяются не компрессоры, а насосы (5 на рисунке 5.5), компактные и более простые по устройству, потребляющие весьма мало энергии для своего привода.

Такой цикл предложен в 50-х годах XIX века почти одновременно шотландским инженером и физиком Ренкиным и немецким физиком Клаузиусом; обычно его называют циклом Ренкина. На рисунке 6.1 изображен обратимый цикл Ренкина в Т-S диаграмме . Схема теплосиловой установки с циклом Ренкина аналогична схеме установки, изображенной на рисунке 5.5, с той лишь разницей, что в случае цикла Ренкина на этой схеме элемент 5 не компрессор, а насос.

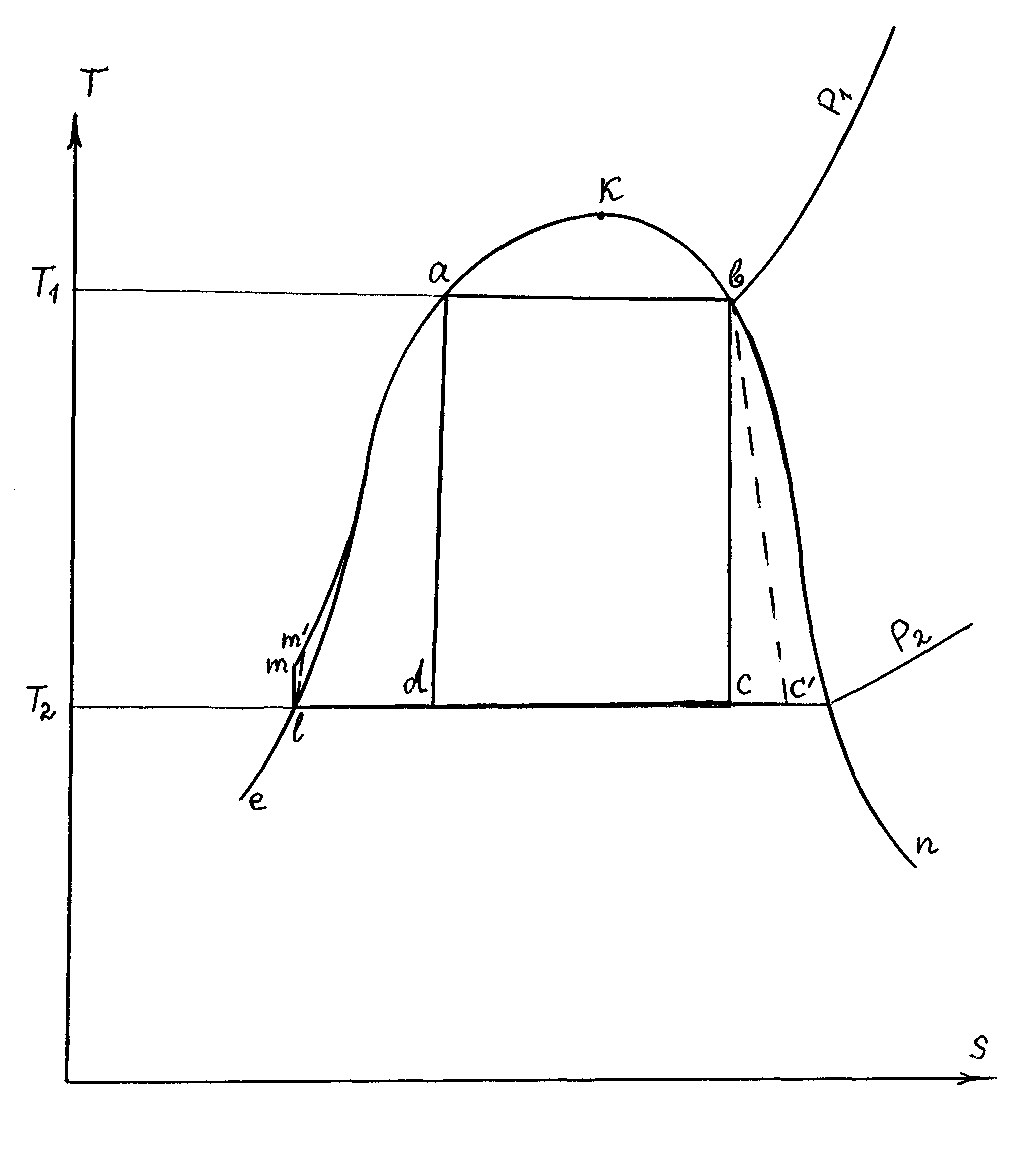
Рисунок 6.1 – Циклы Ренкина и Карно на влажном паре в Т-S диаграмме

Вода сжимается насосом от давления Р₂ до давления Р₁ по адиабате (изоэнтропе) . Длина изоэнтропы в цикле Ренкина весьма мала по сравнению с длиной изоэнтропы в цикле Карно. В области жидкости изобары в Т-S диаграмме (а также и в i-S диаграмме) проходят очень близко друг от друга, поэтому зачастую при изображении цикла Ренкина в этих диаграммах изобары в области жидкости сливаются с левой пограничной кривой .

Посчитаем обратимый пароводяной цикл Ренкина для тех же исходных данных, с которыми мы считали обратимый цикл Карно, т.е. Т₁ = 350 и Т₂ = 25 . Сначала находим энтальпию воды в конце конденсации (в начале сжатия в насосе), в точке « » . Работу сжатия в насосе находим по формуле

, (6.1)

здесь ΔР_нас = Р₁ – Р₂ = 16,54 – 0,003 ≈ 16,54 МПа; ν = 0,001 м³/кг; КПД насоса для обратимого цикла и тогда Δi_нас ≈ 16,5 кДж/кг. Энтальпия воды после сжатия, в точке «m» . Температура на выходе из насоса t_m = f · (P₁, i_m) ≈ 25,4 .

Подводимое в цикле тепло q₁ = i_b – i_m = 2566,1 – 121,2 = 2444,9 кДж/кг. Отводимое в цикле тепло . Энтальпию влажного пара i_c найти затруднительно, поэтому рассчитаем тепло q₂ через энтропии S_c = S_b = 5,2149 кДж/(кг·град); = 0,367 кДж/(кг·град); = 298,15 · (5,2149 – 0,367) = 1445,4 кДж/кг. Термический КПД обратимого цикла Ренкина (вспомним, что ), т.е. термический КПД обратимого цикла Ренкина меньше термического КПД обратимого цикла Карно.

А как необратимость процессов в турбине и насосе скажется на величину КПД цикла Карно.

Разъяснение. С учетом необратимостей процессов в турбине и в насосе (или в компрессоре) КПД цикла снижается и его уже не следует называть термическим КПД. Об этом подробнее будем говорить в другой лекции.

Необратимый цикл Ренкина изображен на рис. 6.1 точками . Пусть внутренний относительный КПД насоса равен и тогда по формуле 6.1 находим работу насоса . Энтальпия воды на выходе из насоса в реальном процессе . Подводимое в цикле тепло . Берем энтропию пара после расширения в турбине, как и для «реального» цикла Карно . Отводимое в цикле тепло . КПД реального цикла Ренкина будет равен . Снижение КПД цикла Ренкина от необратимости не столь резкое, как мы это видели для цикла Карно.

Итак, получен интересный вывод: КПД реального цикла Ренкина выше КПД необратимого цикла Карно (в нашем примере ). И другие потери энергии в реальной установке не повлияют на этот вывод. Забегая вперед, скажем, что наиболее распространенным циклом в реальных ТЭУ (и на органическом и на ядерном топливе) является цикл Ренкина, усложненный различными способами с целью повышения и КПД установки и экономического критерия эффективности.