Список использованных источников

1. Кириллин, В.А. Техническая термодинамика / В.А. Кириллин, В.В. Сычев, А.Е. Шейндлин. – М.: «Энергия», 1974. – 448 с.

2. Белинский, С.Я. Энергетические установки электростанций / С.Я. Белинский, Ю.М. Липов. – М.: «Энергия», 1974. – 304 с.

3. Детская энциклопедия: в 12 т / редколлегия: А. Маркушевич (гл. ред.) и др. – М.: «Педагогика», 1973. – Т.З: Вещество и энергия / И. Петрянов (научн. ред.) – 1973. – 544 с.

4. Андрющенко, А.И. Основы термодинамики циклов теплоэнергетических установок / А.И. Андрющенко. – М.: «Высшая школа», 1985. – 319 с.

Тема 4. Термодинамические процессы в тэу

Реферативное изложение темы

Три начала термодинамики. Круговые процессы (термодинамические циклы). Принцип Карно. Понятия энтальпии, теплоемкости, энтропии. Необратимость реальных процессов. Наиболее вероятное (равновесное) состояние системы. Энтропия, как мерило необратимости. Невозможность вечных двигателей.

Изменение объема тела при нагревании (или при охлаждении) связано с работой, которую производят возникающие в этом процессе силы, проявляющиеся в форме давления на поверхность тела. Работа этих сил в процессе подвода тепла Q называется внешней работой L.

Итак, результатом подвода (или отвода) тепла Q является изменение внутренней энергии и совершение внешней работы.

Q = ΔU + L (4.1)

Эту формулу называют аналитическим выражением первого начала (первого закона) термодинамики. Это выражение устанавливает, что в данном термодинамическом процессе тепло расходуется в двух направлениях: на изменение внутренней энергии и на совершение внешней работы.

Отступление. Открытие этого закона покончило с мечтой некоторых изобретателей: создать вечный двигатель, способный работать без затраты энергии (а из формулы 4.1 прямо видно, что при совершении работы L изменяется и внутренняя энергия ΔU). Первое начало термодинамики часто так и формулируют: вечный двигатель I рода невозможен.

Непрерывность действия тепловой машины обеспечивается тем, что рабочее тело (теплоноситель) с параметрами Р₁, ν₁, Т₁, пройдя последовательно ряд процессов на пути 1-а-2 (в Р-ν диаграмме это процессы с увеличением удельного объема, поэтому их можно назвать процессами расширения; рисунок 4.1) и затем ряд процессов сжатия 2-b-1 с изменением Р, ν и Т, вновь возвращается в точку 1 (исходное состояние), где Р = Р₁, ν = ν₁ и Т = Т₁. Таким образом, рабочее тело (теплоноситель) совершает круговой процесс (1-а-2-b-1), или термодинамический цикл, описывающий изменение термодинамических параметров рабочего тела (теплоносителя) и преобразование тепла в работу в теплоэнергетических установках.

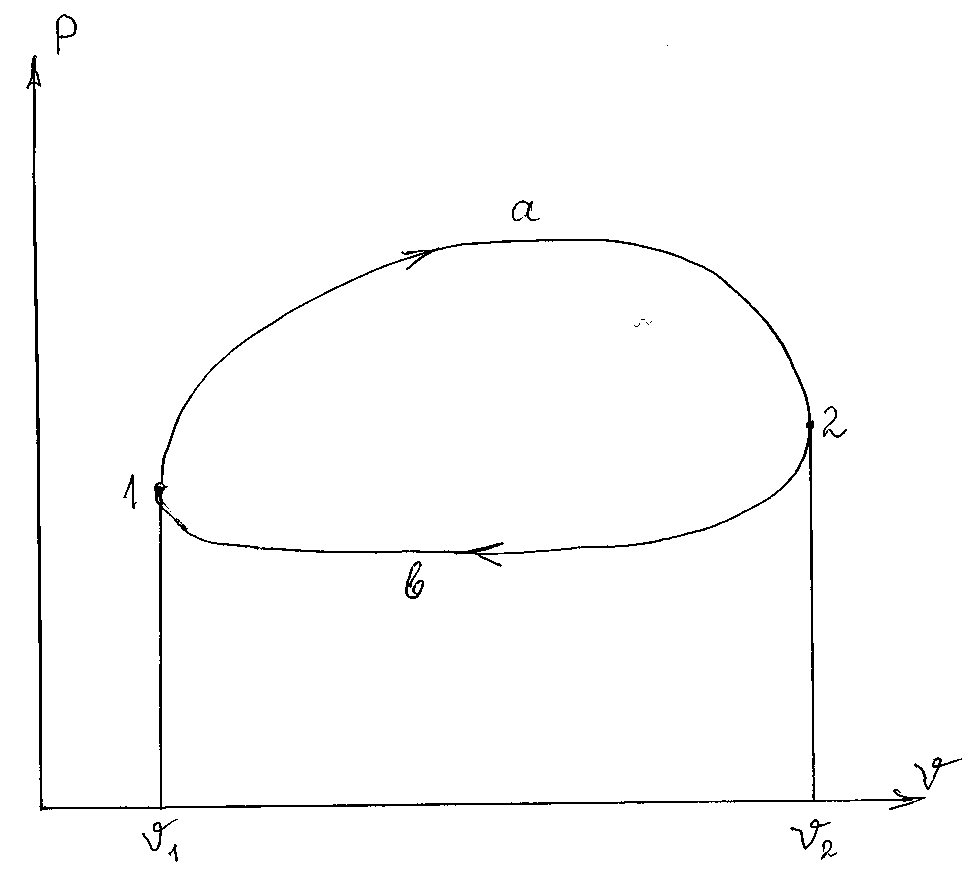
Рисунок 4 – Круговой процесс (термодинамический цикл) в Р-ν диаграмме

На всех диаграммах состояния (P-ν, T-s, i-s) циклы изображают замкнутыми линиями, т.о. суммарное изменение любого термодинамического параметра теплоносителя – рабочего тела в цикле равно нулю. На каждом участке цикла эти параметры изменяются по своим законам, возрастая или понижаясь. Чтобы теплоноситель – рабочее тело в цикле могло вернуться в свое исходное состояние, каждый параметр в цикле должен иметь и положительное и отрицательное приращение. Также обязательными являются процессы, где тепло подводится и отводится.

В Р-ν диаграмме площадь ν₁-1-а-2-ν₂ (рис. 4.1) представляет величину работы расширения, а площадь ν₂-2-b-1-ν₁ – работа сжатия.

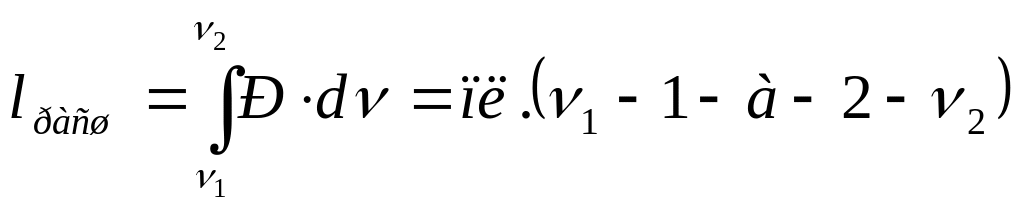(4.2)

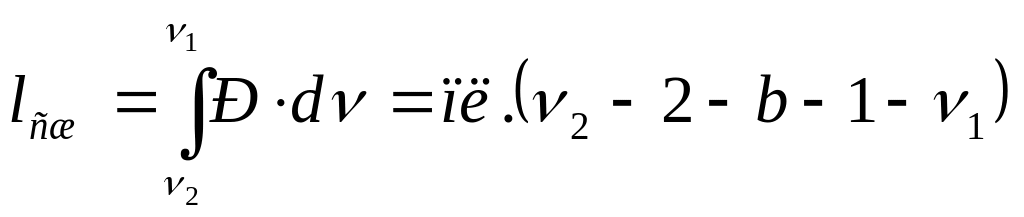(4.3)

В итоге совершения замкнутого кругового процесса (цикла) рабочее тело имеет возможность совершить работу , которая на рисунке 4.1 изображается площадью внутри контура цикла 1-а-2-b-1.

Согласно I закону термодинамики

q_расш = ΔU_расш + _расш (4.4)

Соответственно, для осуществления процессов сжатия отводится тепло

q_сж = ΔU_сж + _сж (4.5)

Поскольку внутренняя энергия есть функция состояния, т.е. величина, не зависящая от пути процесса, то для любого кругового процесса (цикла) ΔU_расш = ΔU_сж, и тогда

_расш – _сж = _ц (4.6)

(=q_подв – q_отв из Т-s диаграммы; об этом будет говориться ниже).

Итак, для осуществления любого кругового процесса (цикла) необходимо наличие не только источника тепла (теплоотдатчика) q_подв, но и холодильника (теплоприемника) q_отв, без которого невозможен возврат рабочего тела – теплоносителя в исходное состояние. Это условие составляет содержание II закона (начала) термодинамики, который может быть сформулирован следующим образом: теплота горячего источника в круговом процессе (цикле) не может быть полностью превращена в работу, так как часть подведенного тепла должна быть передана более холодному источнику (холодильнику). Этот закон можно сформулировать и по-другому: для совершения любого кругового процесса (цикла) необходимо иметь как минимум два источника тепла – горячий и холодный и, следовательно, для этой цели в термодинамической системе необходимо наличие разности температур. Из этих формулировок следует вывод: невозможно создать так называемый вечный двигатель II рода.

В цикле, показанном на рис. 4.1, линии процессов расширения расположены выше линий процессов сжатия (процессы идут по часовой стрелке), вследствие чего _расш  _сж и _ц = _расш – _сж. Такие циклы называют прямыми термодинамическими циклами или циклами теплоэнергетических установок.

Замечание. Обратные термодинамические циклы (циклы холодильных установок и тепловых насосов) нами не рассматриваются.

Открытие второго закона (второго начала) термодинамики связано с французским инженером, физиком С. Карно. Молодой инженер Карно рассчитывал и строил водяные двигатели. Но в это же время во Франции начали широко применять паровые машины, и важнейшей научно-технической задачей стала разработка теории тепловых машин. Хорошо знакомый с расчетом водяных двигателей, Карно уподобил теплоту воде. Чтобы водяная мельница могла молоть зерно (работать), необходимо одно условие: вода должна падать с высокого уровня на низкий. Карно предположил: чтобы теплота могла совершать работу, она тоже должна переходить с высокого уровня на низкий; т.е. по аналогии с разностью высот в водяном двигателе, в тепловой машине должна быть разность температур. Это утверждение называется принципом Карно (высказал он его в 1824 году).

Ниже, в другой теме, будем говорить о коэффициентах полезного действия (КПД) циклов ТЭУ и, в частности, о КПД атомной электростанции, а здесь, забегая вперед, приведем формулу для термического КПД цикла Карно (математическое выражение второго начала термодинамики)

, (4.7)

где Т_Н – температура «верхнего» источника тепла (нагревателя), Т_Х – температура «нижнего» источника (холодильника) в градусах Кельвина. Формула (4.7) наглядно показывает наличие двух источников тепла с различными температурами для привода в действие тепловой машины. Из этого уравнения следует:

1. что для повышения КПД тепловой машины следует уменьшать температуру холодильника Т_х и увеличивать температуру нагревателя Т_н;

2. что термический КПД тепловой машины всегда меньше 1.

Замечание. Цикл Карно обладает еще одним важным свойством, которое позволяет использовать его как эталонный цикл: обратимый цикл Карно имеет наивысший (для данных температур Т_н и Т_х) термический КПД.

Важную роль в самых разнообразных термодинамических расчетах играет величина суммы внутренней энергии системы и произведения давления системы на величину удельного объема системы. Эту сумму называют энтальпией (ее еще называли также теплосодержанием). В удельном массовом виде это

i = U + P · ν, кДж/кг (4.8)

Поскольку новый показатель – энтальпия скомбинирована из величин, являющихся параметрами состояния, то, следовательно, энтальпия также является параметром (функцией) состояния.

Опыт показывает, что количество тепла, подведенное к телу или отведенное от него при данных условиях пропорционально изменению температуры тела по шкале Кельвина (за исключением областей фазовых переходов). Это дает возможность ввести понятие теплоемкости тел. Теплоемкостью называют количество тепла, необходимое для нагревания тела на 1 градус. Теплоемкость единицы количества вещества (массы, объема и т.п.) называют удельной теплоемкостью. Например, для 1 кг газа

dq = c · dT, (4.9)

где с – удельная массовая теплоемкость, имеющая в системе СИ единицу измерения кДж/(кг·град). С математической точки зрения теплоемкость в (4.9) играет роль коэффициента пропорциональности между dq и dT.

Величина удельной теплоемкости зависит от характера процесса и поэтому не является параметром состояния. Таким образом, величины q и c в (4.9) должны быть снабжены индексом, характеризующим вид процесса

C_x = dq_x/dT, (4.10)

где через х обозначен тот параметр, который сохраняется постоянным в данном процессе. Наиболее часто на практике используются теплоемкости изобарного (x = p = const) и изохорного (x = ν = const) процессов; эти теплоемкости называются изобарной и изохорной теплоемкостями. Они обозначаются соответственно С_р и С_ν. В области насыщения и других фазовых переходов (где с изменением dq, Т не изменяется, т.е. dT = 0 значение теплоемкости уходит в бесконечность.

В 1865 г. Клаузиус (немецкий физик) предложил для установления связи между количеством тепла и температурой особую функцию, называемую энтропией (s),

ds = dq/T (4.11)

Энтропия, как и теплоемкость, измеряется в кДж/(кг·град), однако в отличие от теплоемкости обладает свойствами параметров состояния. Подставляя (4.9) в (4.11), получаем связь между энтропией и теплоемкостью

(4.12)

Все реальные процессы, протекающие в действительности (и термодинамические, в частности) необратимы. Их нельзя по желанию провести в прямом и обратном направлении, не оставив никакого следа в окружающем мире (среде). У всех изменений в природе (да и в обществе) есть определенное направление. Общая энтропия всех участников реального процесса может только возрастать, и, таким образом энтропия является мерилом необратимости (внутренней неупорядочности) какого-либо процесса.

Движения молекул беспорядочны (хаотичны), они не могут двигаться в одном направлении, собраться в одном месте, это не вероятно. Наиболее вероятное распределение молекул газа – это равномерное распределение по объему. Наиболее вероятное распределение скоростей молекул – это тоже совершенно определенное равномерное распределение в разных частях системы. Если в системе появляются отклонения (обычно искусственные, принудительные) в концентрации, температуре или давлении, то возникнут самостоятельно идущие процессы выравнивания, и они снова приведут систему в состояние равновесия (упорядоченности) – в наиболее вероятное состояние. Надутый мяч – это искусственно поднятое давление воздуха в данном замкнутом объеме. Надувая мяч, мы «наследили», мы повысили энтропию системы «мяч плюс окружающая среда». Если теперь проткнуть мяч, мы снова «наследим», повысим энтропию; а давление системы выравнится. Самостоятельно мяч не надуется, поскольку система находится в равновесии (более вероятном) состоянии. Любая система стремится перейти из менее вероятного состояния в более вероятное. Вероятностная (статистическая) природа энтропии – это предмет самостоятельного раздела науки – статистической термодинамики, на которую опирается тоже самостоятельная наука – «химическая термодинамика». Для последней большое значение имеет третий закон термодинамики, высказанный немецким физико-химиком Нернстом: по мере приближения температуры любого тела к абсолютному нулю изменение его энтропии при изменении его любого свойства тоже стремится к нулю (s₂ – s₁ → 0). Этот закон позволяет определять абсолютные (отсчитанные от нуля Кельвина) значения энтропии веществ.