Список использованных источников

1. Кириллин, В.А. Техническая термодинамика / В.А. Кириллин, В.В. Сычев, А.Е. Шейндлин. – М.: «Энергия», 1974. – 448 с.

2. Андрющенко, А.И. Основы термодинамики циклов теплоэнергетических установок / А.И. Андрющенко. – М.: «Высшая школа», 1985. – 319 с.

3. Исследование условий конкурентоспособности теплонасосных установок: Отчет о НИР / Институт проблем энергетики НАН Беларуси; научн. рук. А.П. Якушев; отв. исп. Бунин Е.Н. – Минск. – 2001. – № 492. – 36 с.

4. Бунин, Е.Н. Методика сравнения эффективности совместного и раздельного способов производства тепловой и электрической энергии // Весцi НАН Беларусi. Сер. фiз-тэхн. навук. – 2002. – № 1. – С. 115-119.

5. Сравнение водородных энергоустановок с традиционными: Отчет о НИР / ОИЭЯИ-Сосны НАН Беларуси; научн. рук. А.П. Якушев; отв. исп. Бунин Е.Н. – Минск. – 2005. – № 248. – 38 с.

6. Маргулова, Т.Х. Атомные электрические станции / Т.Х. Маргулова. – М.: «Высшая школа», 1978. – 360 с.

7. Ривкин, С.Л. Термодинамические свойства воды и водяного пара. Справочник / С.Л. Ривкин, А.А. Александров. – М.: «Энергоатомиздат», 1984. – 80 с.

Тема 11 Энтропийный и эксергетический методы анализа термодинамических циклов

Реферативное изложение темы

Вывод уравнения Гюи-Стодолы для определения потери работоспособности системы вследствие необратимости процессов, протекающих в ней. T-S диаграмма с источником работы и окружающей средой. Эксергетический КПД отдельных элементов и установки в целом.

Анализируя термодинамические циклы, мы обязаны помнить, что они являются основой функционирования конкретных ТЭУ, состоящих из определенных элементов, в соответствии с процессами, изображаемыми в цикле. Каждый термодинамический процесс, воплощаемый в реальной конструкции, привносит необратимые потери. Постепенный учет этих необратимостей через внутренние КПД элементов оборудования ТЭУ приводит к снижению величины КПД цикла от термического КПД обратимого цикла η_т к внутреннему абсолютному КПД цикла установки и, наконец, к эффективному КПД цикла установки . В принципе учитывает все необратимые потери в цикле данной установки. Однако, для исследователей, желающих оценить вклад отдельных элементов в общую необратимость этого не достаточно, для своей цели они желают воспользоваться тем постулатом, что любая необратимость ведет к увеличению энтропии.

Попытаемся получить уравнение Гюи-Стодолы, на основании которого иногда применяют энтропийный метод расчета потерь работоспособности в необратимых циклах. Изолированная система может произвести работу только в случае, когда она находится в неравновесном состоянии. Если исключить из рассмотрения химические процессы, то для того, чтобы изолированная система могла произвести работу, необходимо, чтобы давления или температуры различных тел, входящих в эту систему, не были абсолютно одинаковыми. В системе, имеющей тела с различными давлениями, отсутствует механическое равновесие. Если в системе есть тела с различными температурами, в ней отсутствует термическое (тепловое) равновесие. Только неравновесная система способна производить работу. По мере производства работы изолированная система будет приближаться к равновесному состоянию.

Представим себе, что в нашем распоряжении имеется изолированная система, состоящая из окружающей среды и некоторого тела или совокупности тел, имеющих отличные от среды давление Р и температуру Т (или один из этих параметров). Такое тело или группу тел будем именовать источниками работы.

Будем предполагать далее, что температура Т₀ и давление Р₀ среды неизменны. Поскольку в общем случае Р  Р₀ и Т  Т₀, то рассматриваемая изолированная система является неравновесной и, следовательно, способна произвести работу. Попытаемся определить максимальную полезную работу системы, или ее работоспособность. Под полезной работой понимается та часть произведенной работы, которая может быть использована по нашему усмотрению. Введем с этой целью следующие обозначения. Обозначим через U₁ и V₁ соответственно внутреннюю энергию и объем источника работы в начальном, неравновесном состоянии, а через U₂ и V₂ – внутреннюю энергию и объем источника работы в конечном равновесном в отношении среды состоянии. Начальное давление и температуру источника работы обозначим через Р и Т, а конечные (равные таковым для среды) – через Р₀ и Т₀.

При совершении работы L внутренняя энергия источника работы изменяется на величину (U₁ – U₂). Часть этой работы теряется в виде тепла Q = T ∙ ΔS и в виде работы сжатия среды Р(V₂ – V₁). Т.о., уравнение для работы можно записать так:

L = (U₁ – U₂) – T ∙ ΔS – Р(V₂ – V₁). (11.1)

Далее в [11.1] изменение энтропии расписывается как уменьшение энтропии для источника работы ΔS = S₁ – S₂ и возрастание энтропии среды на ту же величину ΔS = S₀₂ – S₀₁. Это все верно, а вот дальше «тепло, переданное от источника работы к окружающей среде, равно, очевидно, произведению неизменной температуры среды Т₀ на приращение энтропии среды (S₀₂ – S₀₁)». А еще, через L₀ = P₀(V₂ – V₁) выразим «работу, совершенную источником работы над средой, т.к. давление среды Р₀ по условию неизменно». [11.1; с. 88].

Присваивание величин параметров среды (Т₀, Р₀) и среде и источнику работы нам представляется не «очевидным». Скорее всего, это надо расценивать, как упрощение, которое не всегда может быть оправданным.

С учетом Т₀, Р₀ уравнение (11.1) представляется в двух видах – для случая, когда в системе протекают необратимые процессы (L_полезн) и для случая, когда в системе протекают только обратимые процессы ( ).

L_полезн = (U₁ – U₂) – Т₀ ∙ (S₀₂ – S₀₁) – Р₀ ∙ (V₂ – V₁) (11.2)

= (U₁ – U₂) – Т₀ ∙ (S₁ – S₂) – Р₀ ∙ (V₂ – V₁) (11.3)

Здесь – это максимально возможная полезная работа, которую может произвести данная изолированная система, если процессы, ведущие к установлению равновесия в этой системе, будут протекать обратимо (работоспособность системы), а L_полезн – это величина работы, которую производит та же система в случае необратимости протекающих в ней процессов. Разность этих величин представляет собой потерю работоспособности системы вследствие необратимости процессов, протекающих в этой системе (иногда ее называют энергетической потерей).

– L_полезн = Т₀ ∙ [(S₀₂ – S₀₁) – (S₁ – S₂)] = Т₀ ∙ ΔS_сист,

а, обозначая потерю работоспособности через ΔL, можно написать так:

ΔL = Т₀ ∙ ΔS_сист. (11.4)

ΔS_сист – увеличение энтропии системы в результате протекающих в ней необратимых процессов. Чем больше степень необратимости этих процессов, т.е. больше величина ΔS_сист, тем больше величина потери работоспособности системы; ΔS_сист – суммарное изменение энтропии всех (n) тел, участвующих в процессах. ΔS_сист = , ΔL_сист = .

Уравнение (11.4) называют уравнением Гюи-Стодолы по имени французского физика М. Гюи, который впервые вывел это уравнение в 1889 г., и словацкого теплотехника А. Стодолы, впервые применившего это уравнение для решения технических задач. Определение ΔS_сист – задача не всегда простая, она должна решаться отдельно для каждого реального процесса.

В [11.1; с. 270] вводится понятие коэффициента потери работоспособности

, (11.5)

этот коэффициент показывает, какая доля работоспособности теряется в результате необратимости процессов в ТЭУ.

Если представить себе обратимый цикл Карно, осуществляемый в интервале температур Т и Т₀, тогда величина термического КПД обратимого цикла Карно

или так

(11.6)

Здесь = Т ∙ ΔS – максимально возможное подведенное тепло по изотерме Т = const. q_отв = Т₀ ∙ ΔS – тепло отведенное по изотерме Т₀ = const.

Уравнение (11.6) то же, что и в [11.1; с. 265]. Далее в [11.1] приводится уравнение (9.28) L_полезн = , с которым нельзя согласиться, потому что под q₁ понимается . Поскольку под L_полезн в уравнении (9.28) понимается «полезная работа реального необратимого цикла», то эту работу следует определять не по максимальной температуре подвода тепла Т, а по средней . Т.е. q₁ в уравнении (9.28) лучше обозначить через q_под и определять так

(11.7)

И теперь под относительным коэффициентом работоспособности установки следует понимать

(11.8)

(в [11.1] сомножителя / нет; это ошибка).

С выводом η_ор (его еще иногда называют коэффициентом использования энергии или степенью термодинамического совершенства установки) получили связь эффективного КПД ТЭУ с термическим КПД обратимого цикла Карно, осуществляемого в интервале температур Т и Т₀ (а в общем случае в интервале температур горячего и холодного источников Т_гор и Т_хол).

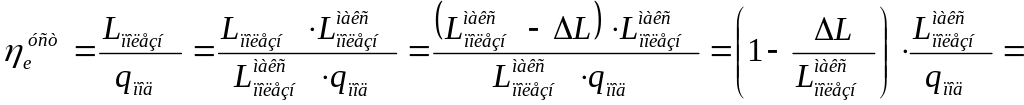
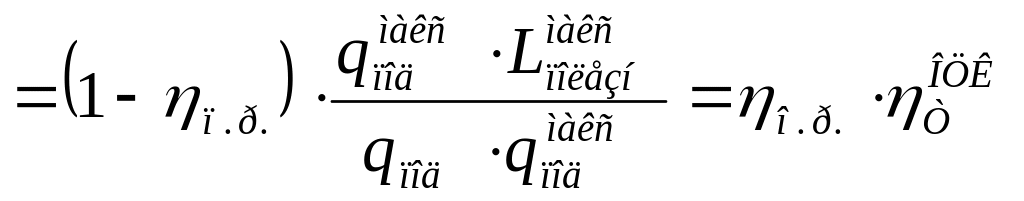(11.9)

В изложенном здесь энтропийном методе расчета потерь работоспособности ТЭУ рассматривалась как изолированная система. При этом сначала вычислялась работоспособность всей установки в целом, а затем подсчитывались величины потерь этой работоспособности в отдельных элементах установки как частях изолированной системы; в этом случае степень термодинамического совершенства того или иного элемента установки оценивается путем сравнения величины потерь работоспособности в этом элементе с величиной работоспособности всей системы в целом.

Возможен иной подход к анализу эффективности работы ТЭУ. Каждый элемент установки можно рассматривать как самостоятельную термодинамическую систему (разумеется, не изолированную, поскольку через этот элемент протекает рабочее тело (теплоноситель), и он обменивается с другими частями установки и теплом, и работой). Эффективность работы элемента можно оценивать путем сравнения работоспособности, которой обладает рабочее тело (или тепло) на входе в этот элемент, с величиной потери работоспособности в результате необратимых процессов, происходящих в элементе; разумеется, работоспособность по-прежнему оценивается по отношению к окружающей среде с параметрами Р₀ и Т₀.

Мы уже знаем, что максимальная полезная работа производится системой, в которой отсутствует равновесие, в том случае, если процессы, ведущие к установлению равновесия, осуществляются обратимо. Если источник работы имеет температуру Т₁ и давление Р₁, а среда Т₀ и Р₀ (см. T-S диаграмму на рисунке 11.1), то этот источник работы может быть обратимо переведен в состояние равновесия с окружающей средой из точки «1» в точку «0», например, следующим путем. Вначале осуществляется обратимый адиабатный процесс, в результате которого температура источника работы снижается от Т₁ до Т₀, а давление при этом снижается от Р₁ до Р_а; затем осуществляется изотермический процесс, в котором за счет теплообмена со средой источник работы достигает давления параметров в точке 0 (этот изотермический процесс обратим благодаря тому, что процесс теплообмена происходит при бесконечно малой разности температур, т.е. при Δt_мин = 0).

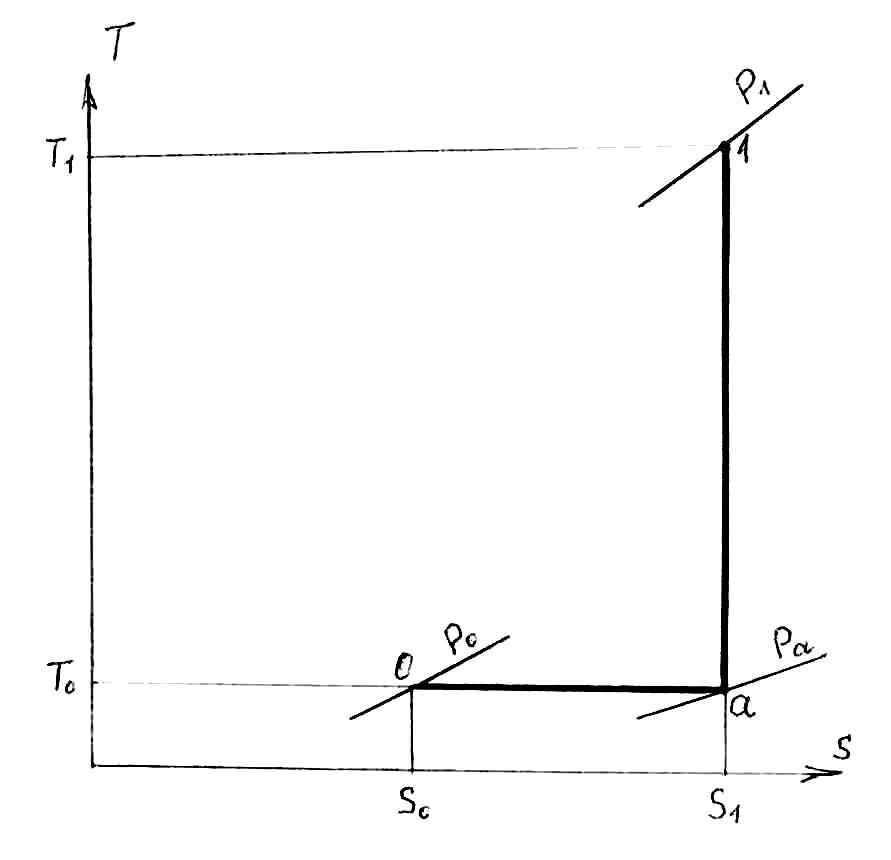
Рисунок 11.1 – T-S диаграмма с источником работы (его параметры

Р₁ и Т₁) и окружающей средой (ее параметры Р₀ и Т₀)

Работа, совершаемая потоком в обратимом адиабатном процессе 1-а, равна:

, (11.10)

здесь i₁ и i_а – энтальпии источника работы (потока) в соответствующих точках. Работа, совершаемая потоком в обратимом изотермическом процессе а-0, определяется следующим соотношением:

(11.11)

Суммарная работа потока в двух обратимых процессах при переходе из состояния 1 в состояние 0, равна

(11.12)

Поскольку работа обратимого изменения состояния источника работы представляет собой максимальную полезную работу (работоспособность) потока, то можно записать

(11.13)

Величину удельной работоспособности потока называют его эксергией, ее обозначают буквой Е

Е = (i – i₀) + T₀ ∙ (S₀ – S) (11.14)

Из этого уравнения следует, что эксергия потока однозначно определена, если заданы параметры этого потока (Р и Т) и параметры среды (Р₀ и Т₀). Термин «эксергия» был предложен в 1956 г., а ранее для обозначения этой величины использовались термины «техническая работоспособность», «максимальная техническая работа» и др. Эксергию можно рассматривать как своеобразную функцию состояния неравновесной системы, состоящей из среды и источника работы в виде потока (а в принципе эксергию можно рассматривать не только для потока, но и для замкнутого объема).

Для количественной оценки степени термодинамического совершенства того или иного аппарата используется понятие так называемого эксергетического КПД, определяемого как

, (11.15)

здесь под Е_вх подразумевается сумма эксергий потока рабочего тела и потока тепла на входе а аппарат; Е_вых – эксергия потока рабочего тела на выходе из аппарата.

Знаменатель в (11.15) иногда называют полной эксергией Е_п = Е_вх – Е_вых, а числитель L_полезн = Е_п – ∑ΔL_i и тогда эксергетический КПД запишется так:

(11.16)

Формулы (11.15) и (11.16) универсально применимы как для отдельного аппарата, так и для установки в целом (для ТЭУ, в частности). Для тепловой машины (например, турбины) эксергетический КПД равен внутреннему относительному КПД машины , а для теплоэнергетической установки эффективному КПД установки .

Следует заметить, что надежды «эксергетиков» на широкое применение эксергетического КПД при анализе термодинамических циклов не оправдались. А попытка использовать принципы эксергетического анализа при условном распределении топлива на комплексных установках по производству тепла и электроэнергии (ТЭЦ) привела вообще к казусу – выходу КПД по производству тепла за 100%. Об этом мы поговорим ниже.