Список использованных источников

7.1 Андрющенко, А.И. Основы термодинамики циклов теплоэнергетических установок / А.И. Андрющенко. – М.: «Высшая школа», 1985. – 319 с.

2. Кириллин, В.А. Техническая термодинамика / В.А. Кириллин, В.В. Сычев, А.Е. Шейндлин. – М.: «Энергия», 1974. – 448 с.

3. Белинский, С.Я. Энергетические установки электростанций / С.Я. Белинский, Ю.М. Липов. – М.: «Энергия», 1974. – 304 с.

4. Варгафтик, Н.Б. Справочник по теплофизическим свойствам газов и жидкостей / Н.Б. Варгафтик. – М.: «Наука», 1972. – 720 с.

5. Ривкин, С.Л. Термодинамические свойства воды и водяного пара. Справочник / С.Л. Ривкин, А.А. Александров. – М.: «Энергоатомиздат», 1984. – 80 с.

Тема 8. Энтальпийно-энтропийная (I-s) и другие расчетные и демонстрационные диаграммы состояния вещества

Реферативное изложение темы

Удобство расчета и наглядность термодинамических процессов на диаграммах. Разные формы линий насыщения в i-s диаграмме. Пограничные кривые двухфазных областей состояний вещества. Критическая и тройная точки. t-i диаграмма. Вид трехмерного термодинамического пространства.

Наряду с таблицами термодинамических свойств, приводимых в [8.1, 8.2] и других справочниках, для выполнения расчетов различных термодинамических процессов (в том числе и термодинамических циклов) оказывается удобным применять диаграммы состояния исследуемых веществ. Важное преимущество диаграмм перед таблицами заключается в наглядности диаграмм, позволяющего широко использовать их для качественного анализа процессов. Еще одно преимущество диаграмм – непрерывность кривых, отображающих плавное изменение термодинамических свойств, тогда как в таблицах свойства приведены дискретно в узловых точках, а между этими точками свойства приходится находить интерполяцией, что чревато снижением точности расчетов.

Наглядность теплот подвода и отвода тепла, работы цикла мы уже наблюдали при изображении циклов в T-S диаграмме (рис. 5.1, 5.2, 5.3, 5.6, 6.1). Обычно рассматриваются лишь области жидкого и газообразного состояния вещества, поскольку диаграммы состояния веществ именно в этих областях чаще всего необходимы для технических расчетов. Для того, чтобы дать представление о том, как изображаются области всех агрегатных состояний вещества (твердая, жидкая и газообразная фазы; двухфазные области, фазовые переходы; линия плавления – затвердевания, испарения – конденсации, линия сублимации, критическая и тройная точки) обратим внимание на две T-S диаграммы. Тройная – точка, в которой сосуществуют твердая, жидкая и газовые фазы. (Некоторые вещества в твердом состоянии могут иметь не одну, а несколько фаз. У таких веществ может быть несколько тройных точек [8.3]). Понятия «фаза» и «агрегатное состояние» различаются; об этом подробнее сказано в [8.3]. Ту тройную точку, в которой вещество сосуществует в трех агрегатных состояниях, иногда называют главной тройной точкой.

На рисунке 5.4 изображен изобарный процесс нагревания (или охлаждения) какого-либо вещества от абсолютного нуля и до какой-то температуры газообразного состояния. Фазовые переходы происходят при постоянной температуре (изотермически). Мы уже упоминали о левой и правой пограничных кривых линии насыщения, ограничивающей область насыщения (область влажного пара). А также есть левые и правые пограничные кривые двухфазных областей: «твердое тело – жидкость» и «твердая фаза – пар». Это схематично показано на рис. 8.1 в T-S диаграмме.

Kc и Kd – левая и правая пограничные кривые двухфазной области «жидкость – пар». При нагревании Кс – линия начала испарения, а Kd – линия окончания испарения; при охлаждении Kd – линия начала конденсации, а Кс – линия окончания конденсации. mb и nc – левая и правая пограничные кривые двухфазной области «твердое тело – жидкость» (линия плавления – затвердевания); ba и de – левая и правая пограничные кривые двухфазной области «твердая фаза – пар» (линия сублимации).

Слева от линии mba расположена область твердой фазы; между линиями nc и Kc – область жидкого состояния; а справа от линии Kde – область газообразного состояния вещества. К – критическая точка.

Рисунок 8.1 – Пограничные кривые, ограничивающие двухфазные области всех трех агрегатных состояний вещества

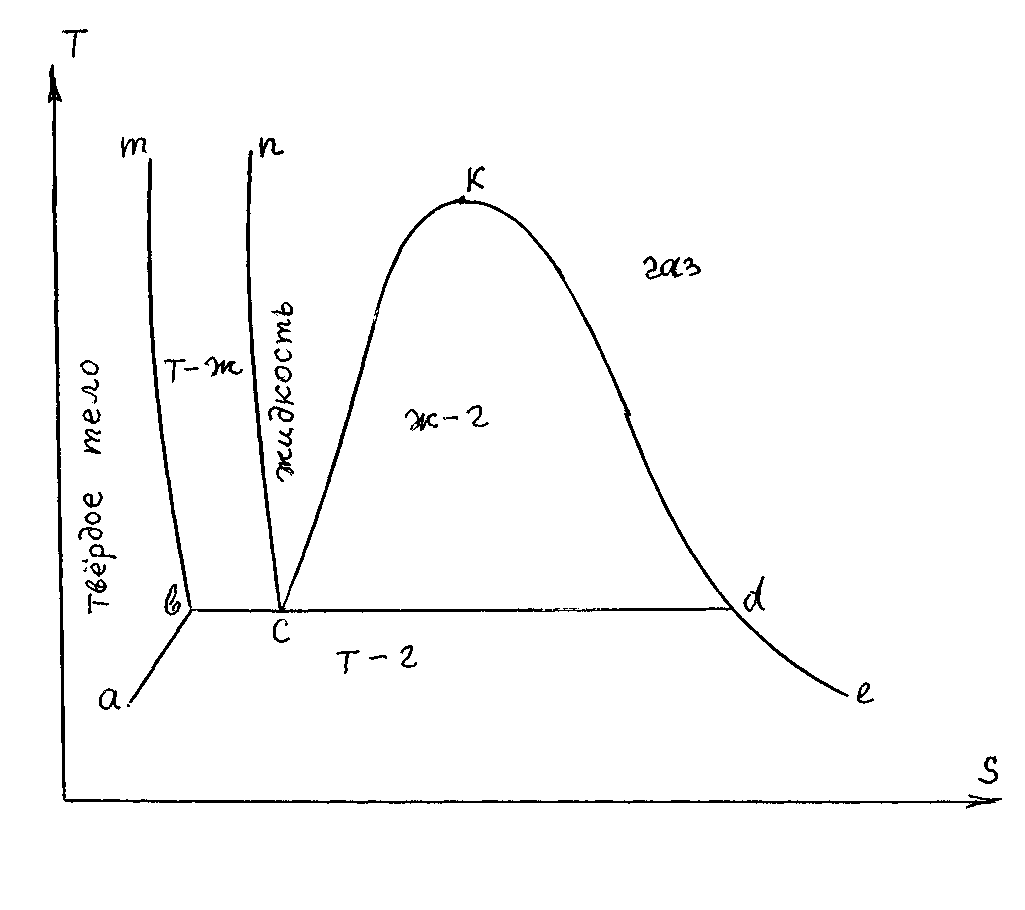
Несмотря на присутствие на рисунке 8.1 всех трех фаз состояния вещества, показать тройную точку затруднительно (она разворачивается в линию bcd). В Р-Т диаграмме тройная точка и все три агрегатных состояния вещества показаны на рисунке 8.2 для четырехокиси азота. Для Н₂О тройная точка соответствует Т = 273,16 К и Р = 0,6108 кПа.

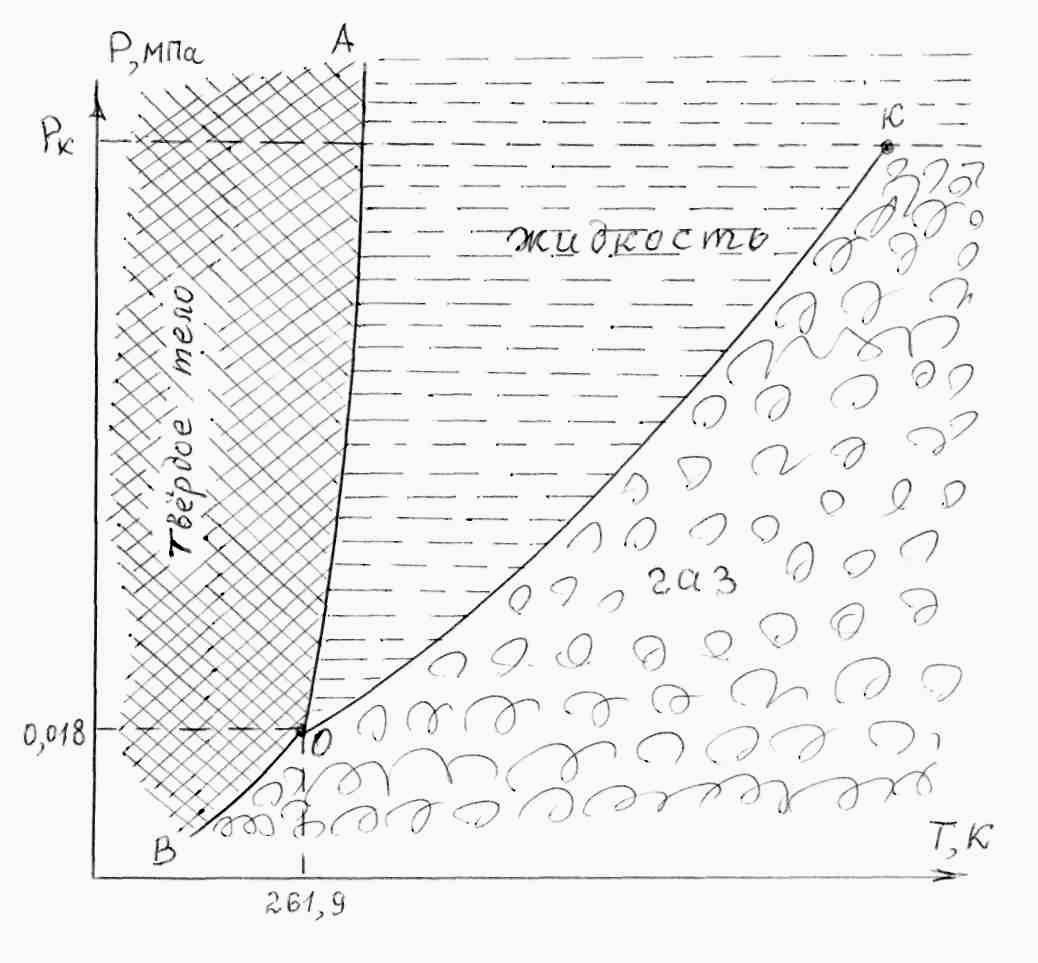
Рисунок 8.2 – Тройная точка (О) и кривые раздела фаз для N₂O₄

в Р-Т диаграмме

От тройной точки расходятся три линии. ОК – кривая кипения (конденсации); ее еще называют кривой (или линией) насыщения; она оканчивается в точке К, называемой критической точкой. При давлении выше Р_к вещество находится в сверхкритическом (условно в жидком) состоянии. ОА – кривая плавления (затвердевания); она уходит вверх и не оканчивается даже при сверхвысоких давлениях (порядка десятков тысяч мегапаскалей). Кривая сублимации ОВ продолжается вниз в сторону низких температур, (вероятно вплоть до абсолютного нуля).

Понятно, что Р-Т диаграммы разных веществ различны. Из рисунка 8.2 видно, что линия насыщения и линия сублимации имеют положительный наклон, т.е. с ростом давления температура фазового перехода (сублимация и кипение – при нагревании, или сублимация и конденсация – при охлаждении) повышается. Такая закономерность справедлива для всех известных чистых веществ [8.3]. А вот линия плавления для различных веществ может иметь как положительный, так и отрицательный наклон. Например, для N₂O₄ наклон линии плавления положительный (рис. 8.2), для Н₂О (льда – воды) наклон этой линии слегка отрицательный; а для СО₂ практически вертикальная в Р-Т диаграмме [8.3].

Следует иметь в виду, что плоские диаграммы являются проекциями трехмерной термодинамической поверхности состояния на одну из трех координатных плоскостей. В качестве примера на рисунке 8.3 изображена термодинамическая поверхность состояния в системе координат Р, ν, Т (следует заметить, что возможны и другие координаты в трехмерном термодинамическом пространстве).

Рисунок 8.3 – Трехмерное термодинамическое пространство

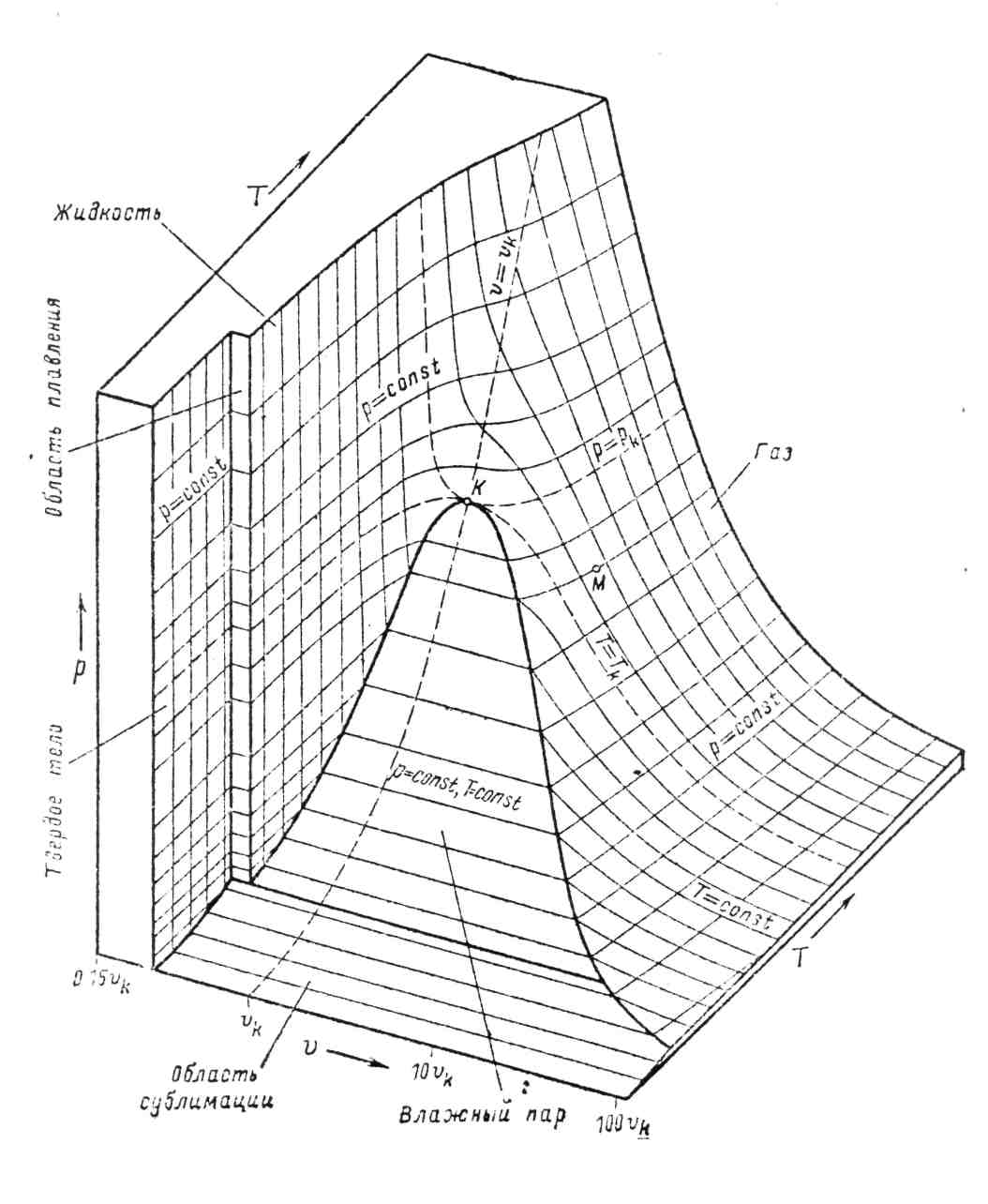
в Р, ν, Т координатах

В теплотехнических расчетах (в первую очередь в расчетах теплосиловых и холодильных установок) широкое применение находит энтальпийно-энтропийная (i-s) диаграмма. Эта диаграмма была впервые предложена в 1904 году немецким теплотехником Р. Молье. В i-s диаграмме на рисунке 8.4 показаны лишь области газообразного и жидкого состояний вещества, представляющие наибольший интерес для теплотехнических расчетов. Рассмотрим основные особенности этой диаграммы.

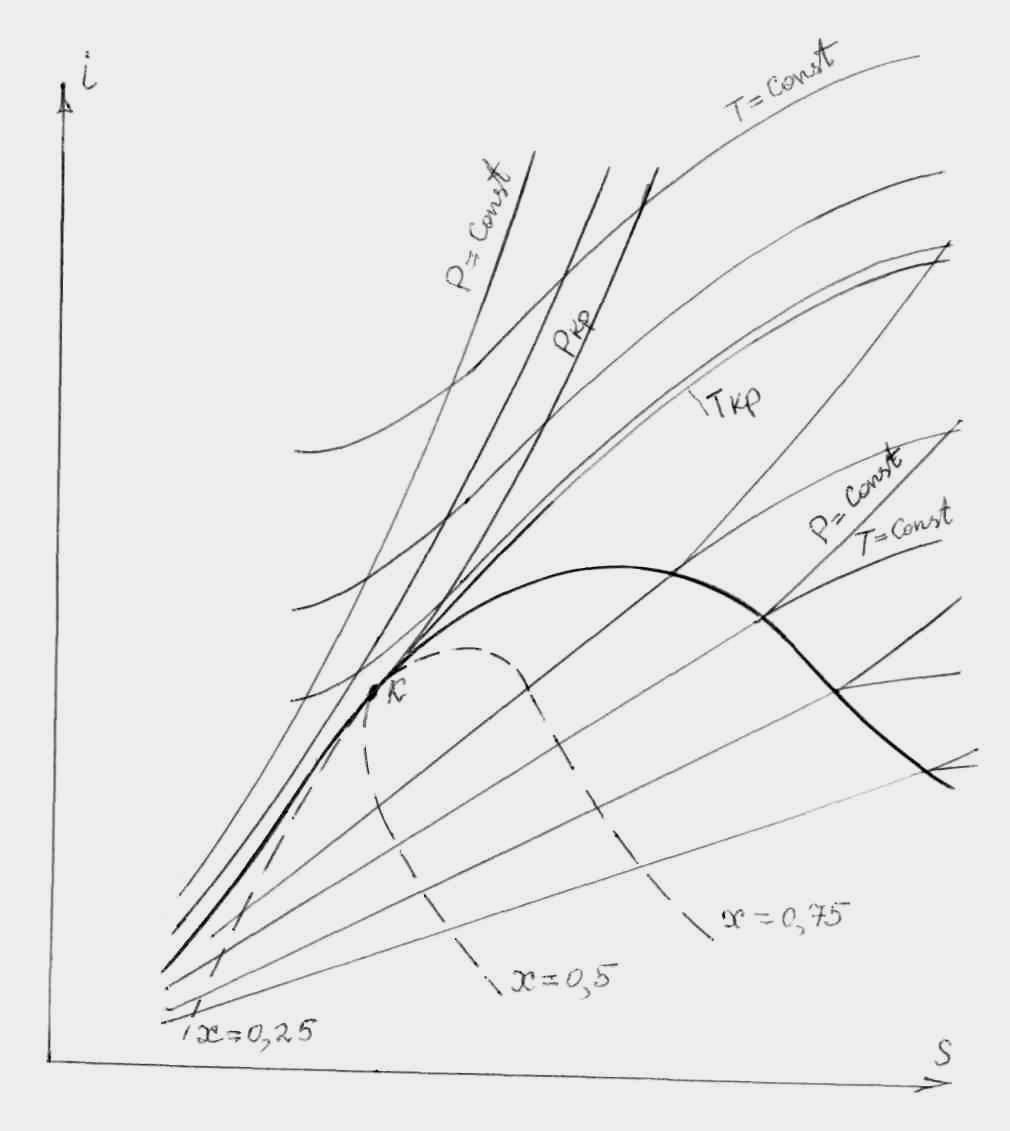
Рисунок 8.4 – i-s диаграмма для вещества типа Н₂О

Как видно из рисунка 8.4, в i-s диаграмме критическая точка К расположена значительно левее максимума энтальпии на линии насыщения. Тангенс угла наклона касательной к пограничной кривой (линии насыщения) в i-s диаграмме в критической точке равен величине Т_Кр, т.е. _Кр = Т_Кр. В общем случае _р = Т, что означает положительный наклон изобар, т.е. с ростом энтропии на изобаре энтальпия всегда возрастает.

В двухфазной области изобара совпадает с изотермой, причем Т = const. Следовательно, внутри двухфазной области в i-s диаграмме изобары прямолинейны. Чем выше давление насыщения (и, следовательно, чем выше температура), тем круче идет изобара (прямая в области насыщения). В области газообразного состояния изобары искривляются, сохраняя веерность (т.е. постепенное расхождение), но без излома пересекают пограничные кривые. Изотермы пересекают пограничные кривые в i-s диаграмме с изломом, и по мере удаления от верхней (правой) пограничной кривой изотермы асимптотически приближаются к горизонтали i = const.

В i-s диаграмме всегда наносятся линии постоянной сухости (x = const) в двухфазной области, а иногда также изохоры. Кривые степени сухости несут практическую нагрузку, они дают наглядное представление о целесообразности расширения рабочего – тела, ниже некоторой величины давления на выхлопе турбины, т.е. являются ограничивающими факторами.

Для расчета различных термодинамических процессов представляют интерес не абсолютные значения энтропии и энтальпии, а их изменение в этих процессах. Поэтому обычно пользуются значениями этих показателей, отсчитанными от произвольно выбранной точки начала отсчета. Как правило, значение энтропии, энтальпии и внутренней энергии принимают (условно) равными нулю (s = 0, i = 0, u = 0) в каком-то одном состоянии вещества. Так для воды и водяного пара за начало отсчета принята тройная точка (Р = 0,006108 бар, t = 0,01 ).

Следует обратить внимание, что для многих веществ (в том числе и для Н₂О) левая и правая пограничные кривые в T-S диаграмме примерно симметричны (см. рис. 8.1), тогда как в i-s диаграмме (рис. 8.4) правая ветвь линии насыщения (начиная с максимального значения энтальпии) ведет себя гораздо положе левой ветви. А для некоторых веществ правая ветвь линии насыщения в энтропийных диаграммах (T-S, i-s) имеет обратный наклон (см. рис. 8.5). Такой наклон правой ветви в i-s диаграмме предрасполагает к благоприятному ходу изоэнтропы расширения газа, начиная от точки 1, поскольку в процессе расширения происходит удаление от линии насыщения, что благоприятно для лопаток турбины.

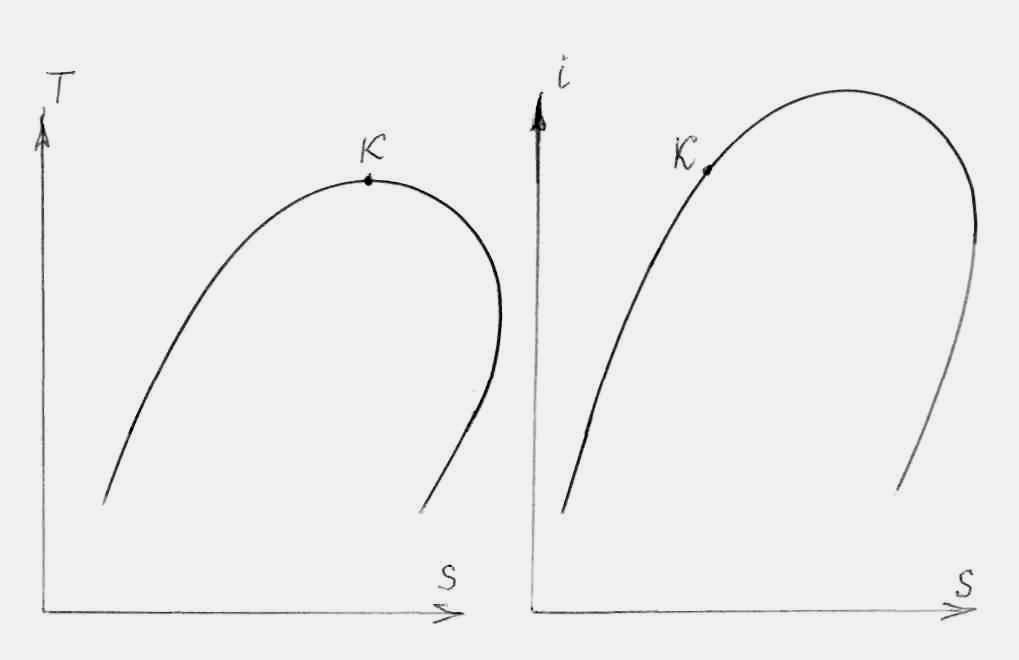
Рисунок 8.5 – Линии насыщения в T-S и i-s диаграммах для некоторых веществ (например, для N₂O₄)

Сложная форма изобар при передаче тепла в теплообменниках приводит к тому, что минимальный температурный напор может быть и на конце и где-то внутри теплообменника. Для наглядности и облегчения поиска сечения теплообменника, где изобары сближаются, хороша t-i диаграмма.

Рисунок 8.6 – t-i диаграмма для вещества типа N₂O₄ и демонстрация сдвига изобары греющего газа (a-b-c) до сближения (Δt_мин) с изобарой обогреваемого газа ( -m-n) в регенеративном теплообменнике с равными расходами теплоносителя по обеим сторонам теплообменника

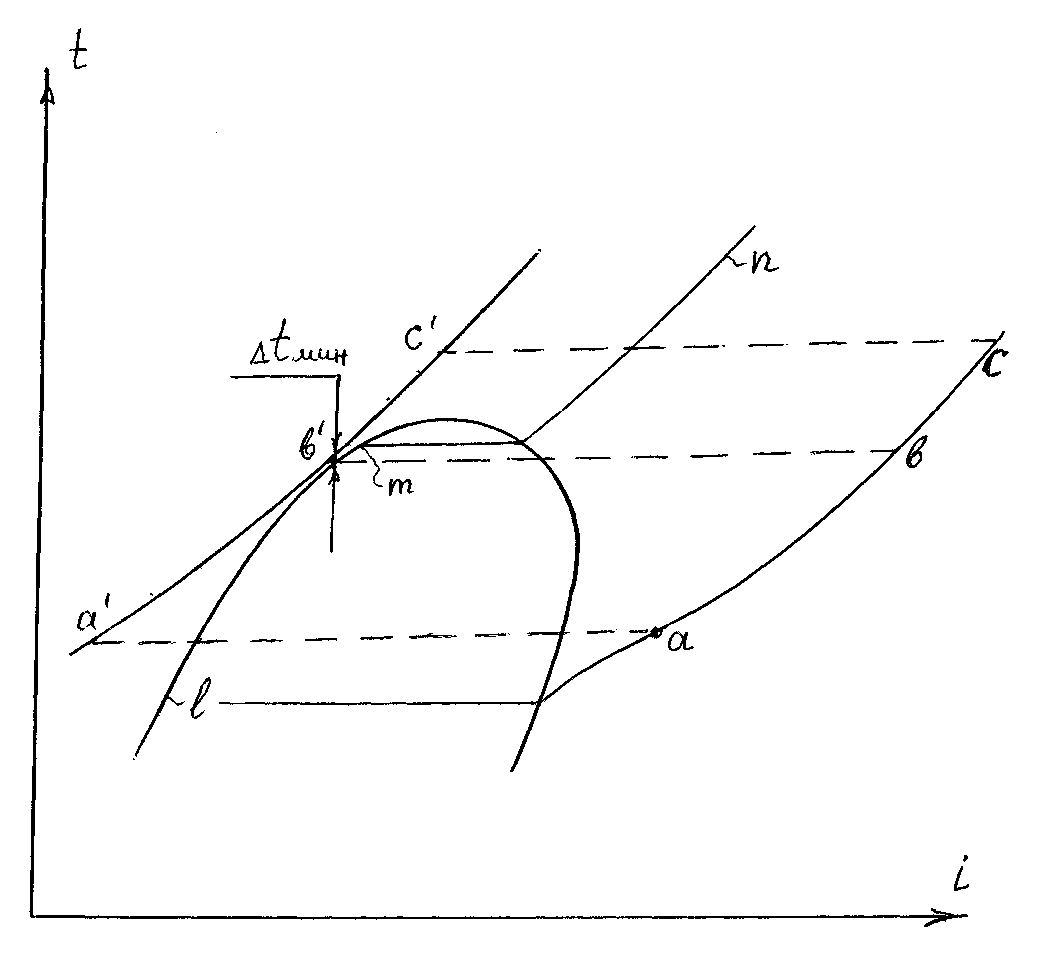
На рисунке 8.6 изображена t-i диаграмма с изобарами полной внутренней (регенеративной) передачей тепла в цикле. Такой регенеративный цикл характерен для одноконтурной АЭС на N₂O₄ (об этом будет идти речь в отдельной теме).

Баланс мощностей в любом теплообменнике предполагает равенство мощностей по обеим сторонам теплообменника, т.е.

N_г = N_об, (8.1)

где «г» – греющая, а «об» – обогреваемая сторона теплообменника. Раскрывая равенство (8.1) через расходы теплоносителей и передаваемое тепло, получаем

G_г · Δi_г = G_об · Δi_об (8.2)

(подобный баланс мы прослеживали и раскрывали при исследовании бинарного цикла в предыдущей теме и там же показывали t-N диаграмму (рис.7.4)). Разделив обе части равенства 8.2 на G_об, получаем

· Δi_г = Δi_об или, обозначая кратность циркуляции m = G_г/G_об,

m · Δi_г = Δi_об (8.3)

В случае G_г = G_об, как это было в регенераторе АЭС на N₂O₄ m = 1 и Δi_г = Δi_об, т.о. t-N диаграмма имеет тот же вид, что и t-i диаграмма. Поэтому сдвигом изобары a-b-c до нового положения a^′-b′-c′, мы находим сечение, где температурный напор (разность температур между греющем и обогреваемом теплоносителями равен задаваемой величине Δt_мин). Чаще всего G_г  G_об и в этом случае сдвигом изобар сечение минимума не найти. Сечение с Δt_мин находится приближениями по формуле 8.3 (расчетно сдвигаясь на i_об и соответственно на m · i_г, в большую и в меньшую сторону).

Ниже, в другой теме, мы будем рассматривать реальные регенеративные циклы, в частности пароводяной цикл ПТУ. Там система регенерации состоит из нескольких регенеративных подогревателей, в которых питательная вода подогревается паром, отбираемым из турбины. Расход пара в этих отборах гораздо меньше расхода питательной воды, что приводит к кратностям циркуляции много меньше единицы. По этой причине изобара греющего теплоносителя идет круто и, поэтому сечение минимума (где Δt_мин) может быть не в точке перегиба (т.е. не в точке перехода воды в пароводяную смесь), а несколько ниже. Это всегда в расчетах следует проверять.