3.4. Расчет показателей экономической эффективности

Проведем расчет следующих показателей:

1. Чистая текущая (дисконтированная) стоимость NPV.

Определим NPV, используя данные таблицы 3.8.

Таблица 3.9

Расчет чистой текущей стоимости инвестиционных проектов

Год	Потоки платежей, характеризующие проект, т.р.		Множитель дисконтирования при r = 10 %	Потоки платежей с дисконтированием, т.р.
	А	Б		А	Б
0	-8000	-10000	1	-8000	-10000
1	2846,4	2820,8	0,909	2587,4	2564,1
2	2952,8	2714,4	0,826	2439	2242,1
3	3348	3216	0,751	2514,3	2415,2
4	3895,2	3558	0,683	2660,4	2430,1
5	5576	5830	0,621	3462,7	3620,4
Итого NPV				5663,8	3271,9

2. Рентабельность инвестиций.

PI = PV / I₀.

PV₁ = 5663,8 + 8000 = 13663,8 т.р. PV₂ = 3271,9 + 10000 = 13271,9 т.р.

PI₁ = 13663,8 / 8000 = 1,708. PI₂ = 13271,9 / 10000 = 1,327.

Оба полученных результата соответствуют нормативному значению PI>1, поэтому рассматриваемые проекты можно принять.

3. Внутренняя норма рентабельности IRR.

Чтобы определить значение IRR с помощью таблиц, выбирают два значения коэффициента дисконтирования r₁<r₂ таким образом, чтобы в интервале (r₁, r₂) функция NPV = f (r), меняла свое значение с плюса на минус или с минуса на плюс. Далее применяют формулу:

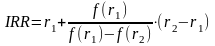, где r₁ – значение табулированного коэффициента дисконтирования, при котором значение f (r₁) > 0 (f (r₁) < 0);

r₂ – значение табулированного коэффициента дисконтирования, при котором значение f (r₂) < 0 (f (r₁) > 0).

Возьмем два произвольных значения коэффициента дисконтирования: r₁ = 15 %, r₂ = 35 %. Соответствующие расчеты приведены в таблице 3.10.

Таблица 3.10

Исходные данные для расчета показателя IRR для первого проекта

Год	Потоки платежей, т.р.	Расчет 1		Расчет 2
		r1 = 15 %	NPV		r2 = 35 %	NPV
0	-8000	1	-8000		1	-8000
1	2846,4	0,87	2476,4		0,741	2108,4
2	2952,8	0,756	2232,3		0,549	1620,2
3	3348	0,658	2203		0,406	1360,8
4	3895,2	0,572	2228,1		0,301	1172,7
5	5576	0,497	2771,3		0,223	1243,5
			3911,1			-494,4

Значение IRR рассчитывается следующим образом.

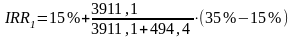= 32,76 %.

Таблица 3.11

Исходные данные для расчета показателя IRR для второго проекта

Год	Потоки платежей, т.р.	Расчет 1		Расчет 2
		r1 = 15 %	NPV		r2 = 25 %	NPV
0	-10000	1	-10000		1	-10000
1	2820,8	0,87	2454,1		0,8	2256,6
2	2714,4	0,756	2052,1		0,64	1737,2
3	3216	0,658	2116,1		0,51	1646,6
4	3558	0,572	2035,2		0,41	1457,4
5	5830	0,497	2897,5		0,33	1910,4
			1555			-991,8

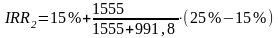= 21,11 %.

4. Срок окупаемости инвестиций.

Он определяется как период времени, в течение которого инвестиции будут возвращены за счет чистых дисконтированных доходов, полученных от реализации инвестиционного проекта.

DPP = n, при котором .

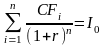Величина DPP определяется путем последовательного суммирования дисконтированных доходов до тех пор, пока не будет получена сумма, равная объему инвестиций или превышающая ее. Из таблицы 3.9 имеем:

Проект 1. При n = 4 имеем сумму 10201,1 т.р. > 8000 т.р. Значит, DPP = 4.

Проект 2. При n = 5 имеем сумму 13271,9 т.р. > 10000 т.р. DPP = 5.

Таким образом, дисконтированный срок окупаемости проектов DPP соответственно равен 4 и 5 лет.

Недисконтированный срок окупаемости PP также найдем из таблицы 3.9:

Проект 1. При n = 3 имеем сумму CF_i = 9147,2 т.р. > 8000 т.р. PP = 3.

Проект 2. При n = 4 имеем сумму 12309,2 т.р. > 10000 т.р. PP = 4