25.3. Теоретические сведения и методические указания

Теоретические положения метода эквивалентных синусоид изложены ра­нее в 24.3.

Вольт-амперная характеристика нелинейной катушки U_L=f(I) может быть рассчитана по заданной вебе­р-амперной характеристикой i()=a·sh(b·) в пред­по­ложении, что напряжение на ее зажимах изменяется по синусоидаль­ному за­кону u_L(t) = U_m ·sin(t+90^о). По закону электромагнитной индукции u_L=е =d/dt, от­куда следует (t) = u_L·dt = _m·sint, где амплитуда потокосцеп­ле­ния равна _m= = 0,045·U. Ток в катушке находится по уравнению вебер-ам­пер­ной ха­рактеристики, после разложения в гармонический ряд получим гармо­ни­ческий состав этой функции: i(t) = a·sh(b·_m·sint) = I_1m·sint + I_3m·sint + I_5m·sint+... Действующее значение несинусоидального тока опреде­ляется через его гармоники по формуле: . В иссле­дуемой цепи форма на­пряжения на катушке будет существенно отличаться от синусоидаль­ной, по­этому результаты измерений могут не совпадать с анало­гичными дан­ными, по­лученными по методу эквивалентных синусоид.

В графических методах расчета используется графическая форма задания вольт-амперных характеристик нелинейных элементов. Для этой цели вольтам­перные характеристики всех элементов схемы строятся в од­ной системе коор­динат в одном в одном и том же масштабе. Производится сложение отдельных характеристик в соответствии с упрощением (сверткой) схемы.

Для исследуемой схемы графическое сложение вольт-амперных характе­ристик отдельных элементов про­изводится согласно уравнению 2-го закона Кирхгофа в век­торной форме в следующей после­довательности:

1. вольт-амперные характеристики активных элементов U_R=f(I) и U_Ro=f(I) складываются последовательно (по оси U): U_а = U_R + U_Ro;

2. вольт-амперные характеристики реактивных элементов U_L=f(I) и U_C=f(I) вычитаются последовательно (по оси U): U_р = U_L  U_С;

3. полученные в п. 1) и 2) суммарные вольт-амперные характеристики для активных и реактивных элементов складываются последователь­но в квадра­туре, в результате сложения получается входная вольтамперная характери­стика: . Точка решения n на графической диаграмме E=f(I), соот­ветствующая резонансу напряжений, определяется из условия U_LU_С = 0.

В аналитических методах расчета используется математическая форма за­дания вольт-амперных характеристик нелинейных элементов. Составляется сис­тема уравнений Кирхгофа в комплексной форме для расчетной схемы. Сис­тема уравнений Кирхгофа дополняется нелинейными уравнениями аппрокси­мации вольт-амперных характеристик элементов U(I) или I(U). Решение сис­темы нели­нейных алгебраических уравнений может быть вы­полнено методом последова­тельных приближений (вручную или на ЭВМ). Для исследуемой схемы система комплексных уравнений Кирхгофа со­вместно с уравнениями аппроксимации имеет вид:

I = c·U_L + d·U_L⁵ (1)

U_R = I ·R (2)

U_Ro = I·R₀ (3)

U_С = I·( jX_С) (4)

U_К = U_Ro +U_L (5)

E = U_R + U_Ro + U_L  U_С (6)

Один из вариантов решения полученной системы уравнений методом по­следовательных приближений представлен ниже.

1. Задаются в первом приближении комплексным значением напряжения на нелинейной катушке, например: U_L=Uе ^j0.

2. Модуль комплексного тока I’ определяется аналитически из уравне­ния (1) или графически по диаграмме функции U_L(I). Аргумент комплексного тока принимают равным 90^о (ток в катушке отстает от напряжения на 90^о). Та­ким образом I = I е ^-j90.

3. По закону Ома определяются напряжения на линейных элементах (ре­зисторах и конденса­торе): U_R = I ·R; U_Ro= I ·R₀.; U_C = I ·(jX_C).

4. Из уравнения (6) находится расчетное значение ЭДС: E = U_R + U_Ro + U_L+ U_C =E·e^j.

5. Сравнивают модуль найденной в первом приближении ЭДС Е с за­дан­ным значением ЭДС Е и с учетом вида полученного неравенства Е Е за­да­ются новым значением напряжения U_L во втором приближении и повто­ряют расчет по тому же алгоритму. Циклы расчета (итерации) повторяют до дости­жения желаемой точности. В результатах последнего цикла корректи­руют аргу­менты комплексных величин путем добавления к ним значения .

Физические процессы в нелинейной цепи переменного тока можно опи­сать системой нелинейных дифференциальных уравнений, составленных для схемы цепи по законам Ома и Кирхгофа и дополненной нелинейными алгеб­раи­ческими уравнениями аппроксимации физических характеристик нелиней­ных элементов. Для исследуемой схемы эта система имеет вид:

u_R + u_Ro + u_L + u_С =e; (1)

u_R = i ·R; (2)

u_Ro = i·R₀; (3)

u_L = ; (4)

i = C· ; (5)

i = a·+b·⁷ . (6)

Решение этой системы уравнений может быть выполнено методами чис­ленного интегрирования на ЭВМ (методы Эйлера, Рунге-Кутта). Суть метода чис­ленного интегрирования состоит в том, что период переменного тока Т раз­бивается на большое число шагов интегрирования, например N=1000, диффе­ренциалы переменных заме­няются конечными приращениями (d  , du  u, di  i, dt  t), а произ­водные переменных  отношением приращений (d/dt  /t, du/dt  u/t). На каждом шаге производится решение сис­темы уравнений и определяются значения переменных величин (токов, напря­жений) и их производных, причем в качестве исходных данных принимают зна­чения некоторых переменных на предыдущем шаге. В качестве таких функций принимают u_С(t), i_L(t), которые определяют запасы энергии в электрическом и магнитном поле, вследствие чего они не могут изменяться скачкообразно. Не­посредственным результатом расчета будут являться массивы значений пере­менных величин (токов, напря­жений) и их производных в заданном интервале времени (например, в течение периода Т). В результате последующей обра­ботки массивов данных могут быть определены действующие, средние, макси­мальные значения переменных, их гармонический состав и другие параметры.

Метод численного интегрирования (численный метод) обладает высокой точностью, так как в нем непосредственно используются физические характе­ристики нелинейных элементов. С появлением ЭВМ и расширением области их применения данный метод является основным при расчете нелинейных цепей как в установившемся, так и в переходном режиме.

Один из вариантов решения полученной системы уравнений методом чис­ленного интегрирования представлен ниже.

Исходные данные:

1) параметры элементов схемы (E_m , , R, R₀, C, a, b);

2) начальные условия [u_С(0)=0, (0)=0];

3) Nчисло шагов интегрирования за период тока; Т- период тока; =2f=2 /T  угловая частота; h=t=T/N  шаг интегрирования.

Алгоритм решения системы уравнений для произвольного к-го шага:

t_к = h·к;

из (6)  i_к = c·sh(b·_(к-1));

из (2)  u_{R к} = i_к ·R;

из (3)  u_{Rо к} = i_к ·R_o;

из (1)  u_Lк = E_m·sin(t_к)  u_Rк  u_Rок u_С(к-1);

из (4)  (d/dt) _к = u_Lк;

из (5)  (du_С/dt) _к = i_к / C;

_к= _(к-1) + h · (d/dt)_к;

u_Ск = u_С(к-1) + h · (du_С/dt)_к.

Конец к-го цикла интегрирования.

Действующие значения токов и напряжений определяются через мас­сивы значений соответствующих функций по формулам

, .

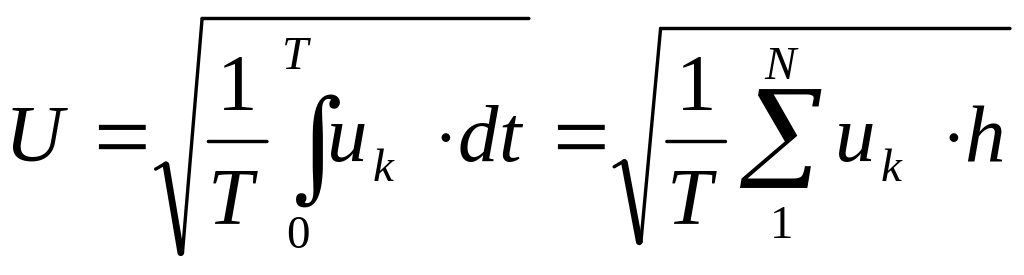Найденные методом численного интегрирования действующие значения токов и напряжений могут существенно отличаться (на 10-20%) от аналогич­ных значений, определенных методом эквивалентных синусоид.

При выполнении экспериментальных измерений можно с достаточной степенью точности считать U_К = U_L , так как активная составляющая этого на­пряжения относительно мала.