Операции с цветом

После выделения некоторого множества возможна его окраска. В командном окне прописывается оператор «color». После него пишется обозначение цвета, которое может задаваться различными способами:

- словесное обозначение цвета (red, green, orange, white, black)

- численное значение цвета в системе RGB ([80,80,255])

- слово «cpk», обозначающее раскраску по типу атомов

- слова «chain», «structure», «temperature»

Палитра и область применения цветовых схем была рассмотрена выше. Таким образом, цветовые схемы, включённые в текстовое меню графического окна могут быть прописаны операторами в командном окне.

Для установки цвета фона используется оператор Background (синтаксис: background <цвет>). Цвет задается вышеописанными способами. При вводе команды «help color» будет предоставлен список предопределенных названий цветов, используемых в RasMol.

Другие операторы и команды

Визуализация дисульфидных мостиков – SSBonds.

Команда используется для представления дисульфидных мостиков белка пунктирными линиями или цилиндрами, между остатками цистеина. Сначала программа распознает структуру белка, затем ищет остатки цистеина.

Синтаксис: ssbonds.

Визуализация водородных связей – HBond.

RasMol показывает только водородные связи остовной цепи (углеродного скелета). Он не способен отображать водородные связи между частями цепи, цепями, лигандами и их сайтами связывания.

Синтаксис:

Mеню Edit -> Select All

Mеню Display -> Backbone

Mеню Colour -> Structure

restrict helix

backbone 0

hbonds 0.5

color hbonds <цвет>

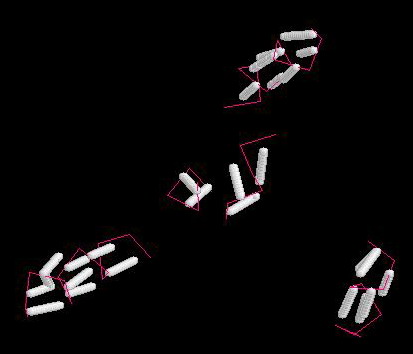
Выделение гирофорных аминокислот.

Синтаксис:

select hydrophobic

color magenta

wireframe 0.4

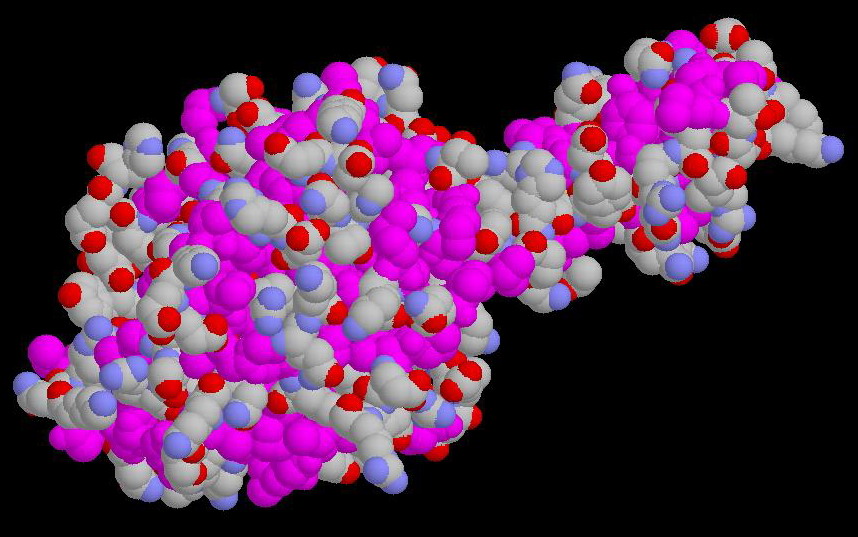
Гидрофобные аминокислоты окрашены в пурпурный цвет, остальная часть молекулы окрашена по CPK.

Показать атомы металлов (атомы кадмия размером в 2,6 Амстронг).

Синтаксис:

Mеню Edit -> Select All

Mеню Display -> Backbone

Mеню Colours -> Chain

select cd

Mеню Display -> Spacefill

Mеню Colours -> CPK

select within(2.6,cd)

Mеню Display -> Spacefill

Mеню Colours -> Cpk

Увеличить масштаб – Zoom.

Позволяет увеличить открытое в данный момент изображение. Так же можно восстановить предний размер. Целочисленный параметр задает увеличение в процентах масштаба «по умолчанию». Минимальное значение параметра – 10, максимальное значение зависит от размера молекулы. Для средних белков это примерно 500.

Синтаксис: zoom 200, zoom off.

Цель работы: ознакомление с работой программы RasMol/

Методика выполнения работы

1) Запустить программу RasMol.

2) В порядке, описанном в методических указаниях, изучить основные компоненты программы.

3) Выполнить задания, приведенные в методических указаниях.

Форма отчета по лабораторной работе №4

1. Название лабораторной работы.

2. Цель работы.

3. Результаты работы при выполнении задания

4. Выводы по проделанной работе.

Лабораторная работа №5. Компьютерное моделирование теплообменной аппаратуры

Методические указания

Процесс передачи тепла через стенку весьма распространен в биотехнологии и значительно влияет на протекание биохимических реакции во всех типах реакторов. Процесс передачи тепла в теплообменной аппаратуре является основным и служит для сообщения технологическому потоку нужной температуры.

Выбирая различные способы оформления реакторов, можно влиять на интенсивность теплообмена между основным (реакционным) потоком и потоком хладоагента или окружающей средой. При полном отсутствии теплообмена через стенку получают адиабатический реактор. Реакторы, имеющие теплообмен с внешней средой, относятся к политропическим.

При рассмотрении процесса передачи тепла от одного теплоносителя к другому через стенку можно выделить несколько элементарных этапов:

- переход тепла от горячего теплоносителя к более холодной стенке,

- поглощение тепла материалом стенки и ее нагрев,

- распределение тепла но объему стенки,

- переход тепла от стенки к холодному теплоносителю.

Если процесс теплообмена протекает стационарно, то температура в каждой точке материала (теплоносителей и стенки) не изменяется во времени. Применение модели с сосредоточенными параметрами (т.е. когда пространственные координаты не входят в математическое описание) приводит к алгебраическим соотношениям между температурами в системе.

Если, наоборот, температуры меняются во времени, математическое описание получается в виде системы обыкновенных дифференциальных уравнений (аргументом является время).

Зависимость температур от геометрических координат обуславливает математическое описание статики в виде обыкновенных дифференциальных уравнений (если пространственная координата одна) или дифференциальных уравнений в частных производных. Независимыми переменными при этом являются пространственные координаты. Динамическая модель при наличии пространственно-распределенных эффектов описывается уравнениями в частных производных, причем одной из независимых переменных является время.

Интенсивность перехода тепла от одного теплоносителя (например, горячего потока жидкости или газа) к другому (стенке) зависит от разности температур между ними, а также от теплового сопротивления. В расчетные уравнения, однако, обычно включают не сопротивление, а обратную ветчину – коэффициент теплоотдачи α – тепловой поток (ккал·ч или Вт) через поверхность площадью 1 м² при разности температур (температурном напоре) 1 градус.

Полный тепловой поток q определяется произведением коэффициента теплоотдачи α на поверхность F и на температурный напор ΔT:

. (5.1)

Уравнение (5.1) применимо как к нагреванию стенки от горячей жидкости, так и, наоборот, к нагреванию холодной жидкости горячей стенкой; при этом ΔT будет иметь разные знаки.

Если пренебречь распространением тепла в стенке, то теплопередачу от горячего потока жидкости к холодному, находящемуся по другую сторону стенки, можно представить как процесс преодоления тепловым потоком двух последовательных сопротивлений теплоотдачи – от горячего потока к стенке и от нагревшейся стенки к холодному потоку.

Используя вместо сопротивлений коэффициенты теплоотдачи (α₁ и α₂), получаем выражение, определяющее коэффициент теплопередачи (К):

. (5.2)

В практических расчетах часто используют коэффициент теплопередачи как характеристику интенсивности теплообмена между потоками:

. (5.3)

В тех случаях, когда коэффициенты теплоотдачи учитываются порознь, принимают усредненную температуру стенки, разделяющей потоки. Иными словами, считают, что теплопроводность материала стенки настолько велика, что перепад температуры отсутствует.

Коэффициенты теплоотдачи зависят от многих параметров, но наиболее сильно – от скорости потока, характера набегания жидкости на стенку, плотности и теплопроводности жидкости. При выполнении точных расчетов зависимость коэффициента теплоотдачи от параметров потока следует учитывать. Однако для большинства инженерных расчетов теплообменной аппаратуры и реакторов достаточны упрошенные представления.

Для вывода уравнений математического описания процесса теплообмена через стенку следует рассмотреть тепловой баланс каждой среды, имеющей запас тепла. Он складывается из прихода и расхода тепла, которые определяют накопление тепла в объеме; накопление является временным процессом:

накопление = приход – расход.

В статике ввиду равенства прихода и расхода тепла накопление равно нулю.

Накопление связано с изменением температуры:

или для элементарного объема:

,

где ρ – плотность;

с_р – удельная теплоемкость;

V – объем;

S – сечение потока;

dl – элементарный участок потока.

Приход и расход тепла может определяться теплоотдачей (теплопередачей), а в случае проточной системы с распределенными параметрами – притоком и уносом тепла с конвективным потоком.

Количество тепла, поступающее в аппарат с конвективным потоком определяется как

или для элементарного объема за элементарное время d:

,

где υ – объемный расход потока.

Количество тепла, уходящее из рассматриваемого объема с конвективным потоком определяется следующим выражением:

или для элементарного объема:

.

Приход тепла, определяемый теплопередачей:

или для элементарного объема за элементарное время:

,

где Т_ВН – температура внешнего теплоносителя.

С учетом полученных соотношений, накопление тепла в системе составит:

или в элементарном объеме за элементарное время:

.

Проведя несложные преобразования, получим уравнение теплового баланса, описывающего динамику теплообменников, во всем объеме которых происходит полное (идеальное) смешение частиц потока:

, (5.4)

где Т₀, Т – температура потока на входе и в зоне идеального смешения.

Соответственно для трубчатых теплообменников, работающих по принципу вытеснения, уравнение динамики будет выглядеть следующим образом:

(5.5)

Ввиду того, что в статическом режиме накопление тепла в системе равно нулю, модель статики теплообменников смешения будет иметь вид:

, (5.6)

статика трубчатых теплообменников описывается уравнением:

, (5.7)

где F – периметр поверхности теплообмена.

Пример 1: Теплообменник представляет собой тонкостенный змеевик, по которому в режиме идеального вытеснения движется охлаждаемый поток жидкости. Змеевик погружен в воду, непрерывно протекающую через сосуд, так что температура охлаждающей воды ТВН практически постоянна и равна 10ºС во всем объеме.

Требуется определить температуру на выходе потока, идущего по змеевику со скоростью ω = 4 м/с, если температура его на входе равна 95ºС, длина трубки змеевика L = 2 м, его сечение S = 10^-4 м², коэффициент теплопередачи К = 1,16·10⁴ Вт/(°С·м²). Теплоемкость охлаждаемой жидкости с_р = 2,93·10³ Дж/(°С·кг), ее плотность ρ = 900 кг/м³. Параметры считать не зависящими от температуры, изменение объема не учитывать. Режим работы считать стационарным.

Температура охлаждаемого потока Т подчиняется дифференциальному уравнению (5.7):

, (5.8)

где l – длина, r – радиус змеевика, S·ω = υ – объемный расход потока.

Начальное условие для уравнения (5.8) Т(0) = 95° С.

Вычислим коэффициент уравнения:

м^-1.

Уравнение (5.8) подлежит решению в пределах изменения независимой переменной l от 0 до 2 м. Температура на выходе потока составила T(L) = 76°C.

Решение представлено на рисунке 5.1.

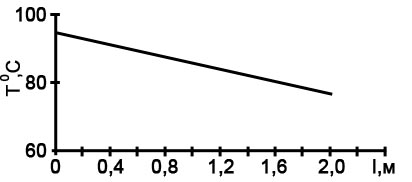
Рисунок 5.1 – Профиль температуры но длине теплообменника

Пример 2: Жидкость охлаждается в теплообменнике типа «труба в трубе». Охлаждаемая жидкость и хладагент движутся параллельно (прямотоком). Требуется определить температуры потоков на выходе теплообменника, если начальная температура охлаждаемой жидкости равна 170ºС, а хладагента 15ºС. Плотность охлаждаемой жидкости и хладагента ρ = 900 кг/м³. Диаметры труб теплообменника: внутренней D₁ = 0,01 м, наружной (для хладагента) D₂ = 0,03 м.

Длина теплообменника L = 1 м. Теплоемкость жидкости и хладагента с_р = 3,35·10³ Дж/(°С·кг). Объемный расход охлаждаемой жидкости υ₁ = 2,28·10^-4 м³/с, хладагента υ₂ = 5,75·10^-4 м³/с, коэффициент теплопередачи К = 4900 Вт (м²·°С). Температурный профиль по длине для каждого из потоков определяется решением системы дифференциальных уравнений:

, (5.9)

, (5.10)

где Т₁ и Т₂ – температура охлаждаемой и охлаждающей жидкости.

Начальные условия: Т₁(0) = 170ºС; Т₂(0) = 15ºС.

После подстановки в уравнения (5.9) и (5.10) численных значений параметров получаем следующую систему:

,

.

Графики решения системы уравнений математического описания статики теплообменника представлены на рисунке 5.2. На нем изображены температурные профили вдоль теплообменника для обоих теплоносителей.

Рисунок 5.2 – Изменение температур теплоносителей по длине прямоточного теплообменника

Можно видеть, что движущая сила процесса сильно меняется по длине, поэтому эффективность использования различных участков теплообменника не одинакова. Температуры теплоносителей на выходе теплообменника равны: Т₁(L) = 64ºC, T₂(L) = 57ºC.

Пример 3: Смоделировать статический режим теплообменника тина «труба в трубе», используя данные, приведенные в примере 2, для случая противотока. Принять полную длину теплообменника L = 2,5 м.

Тепловые процессы в противоточном теплообменнике подчиняются тем же закономерностям, что и в прямоточном. Поэтому математическое описание теплообменника записывается аналогично, однако формально однотипные уравнения для обоих теплоносителей имеют аргументы различного знака:

, (5.11)

, (5.12)

Существенным различием, отражающим иную организацию потоков теплоносителей, является принципиально другое задание условий решения уравнений (5.11) и (5.12) по сравнению с заданием при решении уравнений (5.9) и (5.10).

Совместное интегрирование уравнений (5.11) и (5.12) возможно лишь в одном направлении: либо при l, меняющемся от 0 до L, либо в обратном – от L до 0. При этом в любом случае оговорено лишь одно начальное условие, второе остается неизвестным. Известно лишь, к какому значению в конце решения должна подойти вторая переменная.

Для решения задачи воспользуемся последним обстоятельством и попытаемся отыскать неизвестное начальное условие Т₂(0) с таким расчетом, чтобы условие, заданное для конца решения (граничное условие), было выполнено, т.е. Т₂(L) = 15ºС. Такие задачи при малом числе условий, подлежащих определению, обычно решают методом проб и ошибок.

Задачей поиска начального условия Т₂(0) является выполнение граничного условия T₂(L) при интегрировании системы уравнений (5.11) и (5.12).

Рисунок 5.3 иллюстрирует процесс поиска неизвестного начального условия Т₂(0).

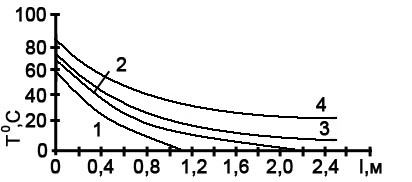
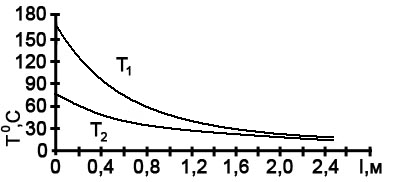
а) б)

Рисунок 5.3 – Результаты моделирования на ЭВМ противоточного теплообменника

а – серия кривых решения системы уравнений (5.9) и (5.10), полученная в процессе определения недостающего начального условия; б – изменение температур теплоносителей по длине теплообменника.

Кривая 1 отражает профиль температуры Т₂, полученный в предположении, что хладагент нагреется до 57ºС (значение взято произвольно). Видно, что это предположении неудачно, так как не получено ожидаемое значение T₂(L) = 15ºC.

Приняв Т₂(0) = 65ºС, получаем кривую 2. Она также неудовлетворительна, так как вместо Т₂(L) = 15ºС получаем лишь 4ºС. Кривые 3 и 4 также не соответствуют искомому начальному условию: в первом случае входная температура T₂(L) получилась заниженной, во втором – завышенной. По-видимому, искомое начальное условие лежит между двумя последними проверенными значениями (70 и 80ºС).

Тщательно исследуя намеченный диапазон задания начального условия, находим Т₂(0) = 75°С.

На рисунке 5.3, б показан результат решения задачи. Выходная температура охлаждаемого потока T₁(L) достигает 18ºС.

Пример 4: Смоделировать переходный режим теплообменника типа «смешение – смешение». Теплообменник представляет собой двухкамерную емкость. В первую камеру емкости поступает охлаждаемая жидкость, во вторую – хладагент. Для обеспечения однородного распределения температуры по объему в камерах установлены мешалки. Плотность охлаждаемой жидкости 850 кг/м³, а хладагента 920 кг/м³. Объемы камер равны и составляют 2,5 м³ каждая. Объемный расход теплоносителя 4,12·10^-3 м³/с, хладагента 5,43·10^-3 м³/с Теплоемкости жидкости и хладагента соответственно 3,75·10³ Дж/(кг·ºС) и 3,14·10³ Дж/(кг·ºС). Поверхность теплообмена составляет 4 м², а коэффициент теплопередачи равен К = 4360 Вт/(м²·ºС). Температура охлаждаемой жидкости на входе меняется скачкообразно от 115 до 200ºС, а температура хладагента от 10 до 15ºС.

Изменение температуры по времени для каждого потока определяется решением системы:

, (5.13)

, (5.14)

где Т₀₁ и Т₀₂ – температуры жидкости и хладагента на входе в теплообменник;

Т₁^*, Т₂^* - температуры потоков на выходе теплообменника для установившегося состояния.

Система уравнений (5.13) и (5.14) решается при начальных условиях: Т₁(0) = Т₁^*; Т₂(0) = Т₂^*.

Для определения Т₁^* и Т₂^* составляются уравнения теплового баланса стационарного режима работы теплообменника:

, (5.15)

. (5.16)

После подстановки численных значений получаем следующую систему:

,

,

которая может быть решена численно или аналитически относительно любых двух переменных, входящих в эти уравнения.

Температуры теплоносителей на выходе теплообменника в установившемся состоянии составили: Т₁^* = 74,46ºС, Т₂^* = 43,93ºС.

Подставляя численные значения в уравнения (5.13) и (5.14) получим систему:

, (5.13)

, (5.14)

Начальные условия: Т₁(0) = 74,46ºС; Т₂(0) = 43,93ºС.

Графики решения системы уравнений математического описания динамики теплообменника представлены на рисунке 5.4. На нем изображены изменения температур во времени для обоих теплоносителей на выходе теплообменника.

Рисунок 5.4 – Изменение температур теплоносителей во времени теплообменника типа «смешение – смешение»

Температуры теплой оси гелей на выходе теплообменника установились через 32 мин и составили Т₁ = 128,57ºС; Т₂ = 73,79ºС

Цель работы: построение математической модели теплообменной аппаратуры.

Методика выполнения работы

1. Составить математическое описание производственного теплообменного аппарата.

2. В зависимости от типа теплообменника смоделировать на ЭВМ статический или динамический режим и определить температурные зависимости для всех теплоносителей.

Форма отчета по лабораторной работе №5

1. Название лабораторной работы.

2. Цель работы.

3. Алгоритм построения модели со всеми необходимыми уравнениями.

4. Алгоритм и программа решения модели на ЭВМ, выполненная с помощью соответствующих прикладных программ.

5. Результаты моделирования в виде графических зависимостей и таблиц.

6. Выводы по проделанной работе.

Лабораторная работа №6. Компьютерное моделирование простых гидравлических систем

Методические указания

Необходимо смоделировать гидравлическую систему, представленную на рисунке 6.1.

Рисунок 6.1 – Моделируемая гидравлическая система

Давления на входах и выходах системы считаются заданными. Также заданы значения коэффициентов пропускной способности. Определить расходы потоков в каждой ветви системы, а также давление в точках разветвления (Р₁₁, Р₁₂, Р₁₃).

,

где Р₁ – давление до сужающего устройства;

P₂ – давление после сужающего устройства.

, (6.1)

, (6.2)

, (6.3)

, (6.4)

, (6.5)

, (6.6)

, (6.7)

Добавить необходимо 3 уравнения, чтобы система имела решение (10 переменных – 10 уравнении).

, (6.8)

, (6.9)

, (6.10)

Составим информационную матрицу. Каждая строка матрицы соответствует определенному уравнению. Каждой неизвестной переменной соответствует определенный столбец. Наличие переменной в том или ином уравнении обозначается символом на пересечении соответствующей строки матрицы соответствующим столбцом (рисунок 6.2).

Номер уравнения	U1	U2	U12	U22	U13	U23	U3	P11	P12	P13	Порядок решения
1											1
2											8
3											4
4											7
5											2
6											5
7											9
8											3
9											6
10											10

– символ обозначает начальное приближение.

– символ обозначает, что данная переменная определяется в данном уравнении при известных значениях остальных переменных.

– символ обозначает, что данная переменная косвенно определена другим уравнением.

Рисунок 6.2 – Информационная матрица

Если получаемое [U₂ (в 8 решении) - U₂ (в 10 решении)] > ε (ошибка вычисления), то методом половинного деления (или каким-либо другим числовым методом) выбрать новое начальное приближение (для данного примера Р₁₁).

Если U₂(8) = U₂(10) или U₂(8) - U₂(11) ≤ ε, то модель определена.

Смоделировать барботажный аппарат, схема которого определена на рисунке 6.3.

Рисунок 6.3 – Схема барботажного аппарата

Условия: давления на входах и выходах известны, также известны коэффициенты пропускной способности.

Определить расходы газа и жидкости через аппарат, давление в аппарате, давление на дне аппарата.

, (6.11)

, (6.12)

, (6.13)

, (6.14)

Неизвестные переменные: U_G, U_L, P, P_h, h, ρ.

, (6.15)

. (6.16)

Плотность газожидкостной эмульсии (ρ) – величина переменная. Плотность жидкости (ρ_Ж) – величина известная.

Составим информационную матрицу (рисунок 6.4).

Номер уравнения	UG	UL	P	Ph	h	ρ	Порядок решения
1							1
2							2
3							3
4							6
5							5
6							4

– символ обозначает начальное приближение.

– символ обозначает, что данная переменная определяется в данном уравнении при известных значениях остальных переменных.

– символ обозначает, что данная переменная косвенно определена другим уравнением.

Рисунок 6.4 – Информационная матрица

Условие окончания алгоритма – U_L(3) = U_L(4) или U_L(3) - U_L(4) ≤ ε.

Цель работы: построение математической модели гидравлической системы.

Методика выполнения работы

1.Определить уравнения расходов через сужающие устройства промышленной гидравлической системы, а также давления в точках разветвления системы.

2.Закончить полученную систему уравнений для расходов до числа неизвестных давлений в точках разветвления уравнениями для узлов гидравлической системы.

3. Решить полученную систему уравнений на ЭВМ

Форма отчета по лабораторной работе №6

1. Название лабораторной работы.

2. Цель работы.

3. Алгоритм построения модели со всеми необходимыми уравнениями.

4. Алгоритм и программа решения модели на ЭВМ, выполненная с помощью соответствующих прикладных программ.

5. Результаты моделирования в виде графических зависимостей и таблиц.

6. Выводы по проделанной работе.

Задания для выполнения лабораторных работ

Лабораторная работа №1

Вариант 1. По опытным данным, снятым с реального технологического объекта и представленным в таблице, построить адекватную модель.

Таблица

№ эксп.	xl	х2	х3	у	№ эксп.	xl	х2	х3	у
1	234,2	34,20	0,23	12,32	11	269,87	69,21	0,41	17,21
2	239,6	36,13	0,24	13,43	12	270,87	69,25	0,43	16,43
3	241,3	39,20	0,25	14,45	13	268,10	68,32	0,35	17,50
4	252,5	41,98	0,26	15,65	14	272,98	71,06	0,51	14,23
5	257,9	45,67	0,27	16,87	15	281,21	73,76	0,53	11,65
6	266,3	49,12	0,28	17,45	16	289,54	75,87	0,57	11,24
7	267,2	52,98	0,29	17,56	17	290,12	79,21	0,61	10,67
8	267,5	67,87	0,30	18,32	18	292,54	80,10	0,54	9,80
9	267,9	68,54	0,32	17,34	19	294,98	82,05	0,52	9,03
10	268,1	68,32	0,35	17,32	20	300,02	85,98	0,53	8,54

Проведены параллельные опыты, в которых выход объекта изменялся следующим образом

у

17,30

17,50

17,40

17,60

17,25

Вариант 2. По опытным данным, снятым с реального технологического объекта и представленным в таблице, построить адекватную модель.

Таблица

№ эксп.	xl	х2	х3	у	№ эксп.	xl	х2	х3	у
1	216,5	106,50	72,53	12,32	11	248,67	141,51	72,71	17,21
2	218,4	108,43	72,54	13,43	12	249,67	141,55	72,73	16,43
3	220,1	111,50	72,55	14,45	13	246,90	140,62	72,65	17,50
4	231,3	114,28	72,56	15,65	14	251,78	143,36	72,81	14,23
5	236,7	117,97	72,57	16,87	15	260,01	146,06	72,83	11,65
6	245,1	121,42	72,58	17,45	16	268,34	148,17	72,87	11,24
7	246,0	125,28	72,59	17,56	17	268,92	151,51	72,91	10,67
8	246,3	140,17	72,60	18,32	18	271,34	152,40	72,84	9,80
9	246,7	140,84	72,62	17,34	19	273,78	154,35	72,82	9,03
10	246,9	140,62	72,65	17,32	20	278,82	158,28	72,83	8,54

Проведены параллельные опыты, в которых выход объекта изменялся следующим образом

у

17,30

17,45

17,32

17,40

17,25

Вариант 3. По опытным данным, снятым с реального технологического объекта и представленным в таблице, построить адекватную модель.

Таблица

№ эксп.	xl	х2	х3	у	№ эксп.	xl	х2	х3	у
1	103,00	106,50	72,53	307,88	11	29,13	141,51	72,71	302,99
2	59,40	108,43	72,54	306,77	12	28,13	141,55	72,73	303,77
3	57,70	11,50	72,55	305,75	13	30,90	140,62	72,65	302,90
4	46,50	114,28	72,56	304,55	14	26,02	143,36	72,81	305,97
5	41,10	117,97	72,57	303,33	15	17,79	146,06	72,83	308,55
6	32,70	121,42	72,58	302,75	16	9,46	148,17	72,87	308,96
7	31,80	125,28	72,59	302,64	17	8,88	151,51	72,91	309,53
8	31,50	140,17	72,60	301,88	18	6,46	152,40	72,84	310,40
9	31,10	140,84	72,62	302,86	19	4,02	154,35	72,82	311,17
10	30,90	140,62	72,65	302,78	20	2,54	158,28	72,83	311,66

Проведены параллельные опыты, в которых выход объекта изменялся следующим образом

у

302,7

302,9

301,5

303,6

302,2

Вариант 4. Но опытным данным, снятым с реального технологического объекта и представленным в таблице, построить адекватную модель.

Таблица

№ эксп.	xl	х2	х3	у	№ эксп.	xl	х2	х3	у
1	103,00	130,10	164,07	307,88	11	29,13	95,09	163,89	302,99
2	59,40	128,17	164,06	306,77	12	28,13	95,05	163,87	303,77
3	57,70	125,10	164,05	305,75	13	30,90	95,98	163,95	302,90
4	46,50	122,32	164,04	304,55	14	26,02	93,24	163,79	305,97
5	41,10	118,63	164,03	303,33	15	17,79	90,54	163,77	308,55
6	32,70	115,18	164,02	302,75	16	9,46	88,43	163,73	308,96
7	31,80	111,32	164,01	302,64	17	8,88	85,09	163,69	309,53
8	31,50	96,43	164,00	301,88	18	6,46	84,20	163,76	310,40
9	31,10	95,76	163,98	302,86	19	4,02	82,25	163,78	311,17
10	30,90	95,98	163,95	302,78	20	2,54	78,32	163,77	311,66

Проведены параллельные опыты, в которых выход объекта изменялся следующим образом

у

308,3

307,5

309,4

306,6

305,7

Вариант 5. По опытным данным, снятым с реального технологического объекта и представленным в таблице, построить адекватную модель.

Таблица

№ эксп.	xl	х2	х3	у	№ эксп.	xl	х2	х3	у
1	60,10	130,10	132,07	-6,52	11	29,13	95,09	131,89	-11,41
2	59,40	128,17	132,06	-7,63	12	28,13	95,05	131,87	-10,63
3	57,70	125,10	132,05	-8,65	13	30,90	95,98	131,95	-11,65
4	46,50	122,32	132,04	-9,85	14	26,02	93,24	131,79	-8,43
5	41,10	118,63	132,03	-11,07	15	17,79	90,54	131,77	-5,85
6	32,70	115,18	132,02	-11,65	16	9,46	88,43	131,73	-5,44
7	31,80	111,32	132,01	-11,76	17	8,88	85,09	131,69	-4,87
8	31,50	96,43	132,00	-12,52	18	6,46	84,20	131,76	-4,00
9	31,10	95,76	131,98	-11,54	19	4,02	82,25	131,78	-3,23
10	30,90	95,98	131,95	-11,52	20	2,54	78,32	131,77	-2,74

Проведены параллельные опыты, в которых выход объекта изменялся следующим образом

у

-11,30

-11,50

-11,40

-11,60

-11,45

Вариант 6. По опытным данным, снятым с реального технологического объекта и представленным в таблице, построить адекватную модель.

Таблица

№ эксп.	xl	х2	х3	у	№ эксп.	xl	х2	х3	у
1	-552,50	130,10	132,07	-6,52	11	-590,20	95,09	131,89	-11,41
2	-560,00	128,17	132,06	-7,63	12	-591,20	95,05	131,87	-10,63
3	-561,70	125,10	132,05	-8,65	13	-588,50	95,98	131,95	-11,65
4	-572,90	122,32	132,04	-9,85	14	-593,30	93,24	131,79	-8,43
5	-578,30	118,63	132,03	-11,07	15	-601,60	90,54	131,77	-5,85
6	-586,70	115,18	132,02	-11,65	16	-609,90	88,43	131,73	-5,44
7	-587,60	111,32	132,01	-11,76	17	-610,50	85,09	131,69	-4,87
8	-587,90	96,43	132,00	-12,52	18	-612,90	84,20	131,76	-4,00
9	-588,30	95,76	131,98	-11,54	19	-615,30	82,25	131,78	-3,23
10	-588,50	95,98	131,95	-11,52	20	-616,50	78,32	131,77	-2,74

Проведены параллельные опыты, в которых выход объекта изменялся следующим образом

у

-10,63

-10,50

-9,70

-9,90

-10,25