Исходные данные

Дана схема автоматической системы регулирования (рисунок 2.1).

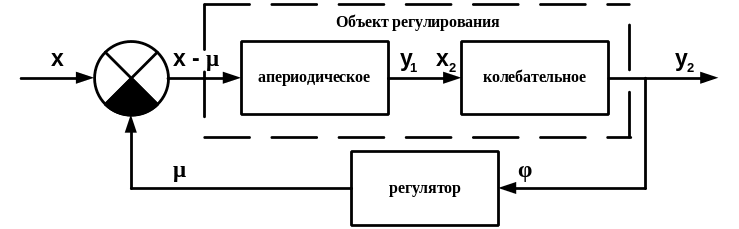
Рисунок 2.1 – Схема АСР

Объект регулирования представлен последоваельностью из двух звеньев

Первое звено: апериодическое

Второе звено: колебательное

Коэффициенты: K = 0,6; T₁ = 4; Т₂ = 1,44; Т₃ = 3.

Коэффициенты регулятора: Кр = 2,5.

Составление дифференциальных уравнений

Первое звено (апериодическое) в дифференциальной форме:

Второе звено (колебательное) в дифференциальной форме:

Передаточная функция объекта регулирования будет определяться комбинацией передаточных функций составляющих ее звеньев, которую можно выразить в виде системы:

Составим дифференциальное уравнение и составим передаточную функцию для регулятора.

В дифференциальной форме:

,

Преобразование системы уравнений

Для построения переходной характеристики объекта управления составим систему, описывающую его:

Учитывая х₁ = 1; х₂ = у₁ имеем:

Для возможности численного решения данной системы уравнений приведем ее к системе дифференциальных уравнений первого порядка. Для этого выполним замену:

Тогда имеем систему дифференциальных уравнений первого порядка. Выполним уединение производных в данной системе, в результате получаем:

Данная система описывает переходный процесс объекта регулирования.

Передаточная функция автоматической системы регулирования будет определяться комбинацией передаточных функций объекта регулирования и регулятора, которую также можно выразить в виде системы:

Для АСР принимаем: х = 1 – μ, у₂ = φ

Для замкнутой АСР система дифференциальных уравнений примет вид:

Выполним замену переменных для преобразования системы и запишем функции для реализации на Visual Basic:

Реализацию решения системы дифференциальных уравнений производим методом Рунге–Кутта 4-го порядка. Предусмотрим построение графика переходного процесса.

Метод Рунге-Кутта 4 порядка столь широко распространен, что его часто называют просто методом Рунге-Кутта.

Рассмотрим задачу Коши. Задача Коши́ – одна из основных задач теории дифференциальных уравнений (обыкновенных и с частными производными); состоит в нахождении решения (интеграла) дифференциального уравнения, удовлетворяющего так называемым начальным условиям (начальным данным).

Задача Коши обычно возникает при анализе процессов, определяемых дифференциальным законом эволюции и начальным состоянием (математическим выражением которых и являются уравнение и начальное условие). Этим мотивируется терминология и выбор обозначений: начальные данные задаются при t = 0, а решение отыскивается при t > 0.

.

При этом х₀ и у(х₀) = у₀ – начальные условия.

Тогда приближенное значение в последующих точках вычисляется по итерационной формуле:

,

где h – величина шага сетки по x и вычисление нового значения проходит в четыре этапа:

,

Этот метод имеет четвертый порядок точности, т.е. суммарная ошибка на конечном интервале интегрирования имеет порядок O(h⁴) (ошибка на каждом шаге порядка O(h⁵)).

Графики данной системы, построенные программой, будут иметь следующий вид (рисунок 2.2):

Рисунок 2.2 – Переходные характеристики объекта управления и замкнутой АСР

Цель работы: решение системы дифференциальных уравнений с помощью метода Рунге-Кутта.

Методика выполнения работы

1. Составить дифференциальные уравнения для объекта регулирования и АСР.

2. Составить алгоритм решения.

3. Составить программу для решения системы уравнений и построения переходных процессов.

Форма отчета по лабораторной работе №2

1. Название лабораторной работы.

2. Цель работы.

3. Порядок составления системы дифференциальных уравнений.

4. Алгоритм и программа на ЭВМ, выполненная с помощью соответствующих прикладных программ.

5. Результаты в виде графических зависимостей и таблиц.

6. Выводы по проделанной работе.

Лабораторная работа №3. Компьютерное моделирование процессов периодического культивирования микроорганизмов.

Методические указания