ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ РФ

ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ВЯТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

Биологический факультет

Кафедра биотехнологии

Д.А. Кропачев

КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ БИОТЕХНОЛОГИЧЕСКИХ ПРОИЗВОДСТВ

Методические указания к лабораторным работам

Киров 2009

УДК 517.958:57

К 83

ИНПИ ВятГУ

Кропачев Д.А. Компьютерное моделирование биотехнологических производств : Методические указания к лабораторным работам. – Киров: Изд-во ВятГУ, 2009. – 64 с.

Настоящее издание является частью учебно-методического комплекса по дисциплине «Компьютерное моделирование биотехнологических производств». Приведены методические указания по выполнению и защите лабораторных работ, приведены контрольные вопросы для самостоятельного изучения.

Предназначены для студентов специальности 240901 «Биотехнология».

Редактор

Подписано в печать Усл.печ.л.

Бумага офсетная Печать матричная

Заказ № Тираж Бесплатно

Текст напечатан с оригинала-макета, представленного автором

________________________________________________________________

610000, г. Киров, ул. Московская, 36

Оформление обложки, изготовление – ПРИП ВятГУ

© Вятский государственный университет, 2009

© Д.А. Кропачев, 2009

Содержание

Лабораторная работа № 1. Построение математических моделей 4

Методические указания 4

Методика выполнения работы 13

Форма отчета по лабораторной работе №1 13

Лабораторная работа №2. Решение дифференциальных уравнений. 15

Методические указания 15

Методика выполнения работы 18

Форма отчета по лабораторной работе №2 18

Лабораторная работа №3. Компьютерное моделирование процессов периодического культивирования микроорганизмов. 19

Методические указания 19

Методика выполнения работы 27

Форма отчета по лабораторной работе №3 27

Лабораторная работа №4. Компьютерное моделирование биологических объектов 29

Методические указания 29

Методика выполнения работы 39

Форма отчета по лабораторной работе №4 39

Лабораторная работа №5. Компьютерное моделирование теплообменной аппаратуры 40

Методические указания 40

Методика выполнения работы 47

Форма отчета по лабораторной работе №5 48

Лабораторная работа №6. Компьютерное моделирование простых гидравлических систем 49

Методические указания 49

Методика выполнения работы 52

Форма отчета по лабораторной работе №6 52

Задания для выполнения лабораторных работ 53

Лабораторная работа №1 53

Лабораторная работа №2 56

Лабораторная работа №3 56

Лабораторная работа №4 56

Лабораторная работа №5 57

Лабораторная работа №6 58

Вопросы для контроля знаний 61

Лабораторная работа № 1. Построение математических моделей Методические указания

1. Построение математической модели технологического аппарата экспериментальным методом

В тех случаях, когда информации о рассматриваемом процессе недостаточно или процесс настолько сложен, что невозможно составить его детерминированную модель, прибегают к экспериментально-статистическим методам. При этом процесс рассматривают как «черный ящик». Различают пассивный и активный эксперименты.

Пассивный эксперимент является традиционным методом, в соответствии с которым ставится большая серия опытов с поочередным варьированием каждой из переменных. К пассивному эксперименту относится также сбор исходного статистического материала в режиме нормальной эксплуатации технологического процесса.

Активный эксперимент ставится по заранее составленному плану (планирование эксперимента), при этом предусматривают одновременное изменение всех переменных, влияющих на процесс, что позволяет сразу установить силу взаимодействия переменных и на этом основании сократить общее число опытов.

Метод наименьших квадратов

Постановка задачи. Объект имеет m входных х₁, х₂..., х_m и одну выходную координату у. Структурная схема такого объекта приведена на рисунке 1.1.

Рисунок 1.1 – Структурная схема объекта

Здесь мы не делаем различия между регулируемыми и нерегулируемыми переменными. Обозначим х = (х₁, х₂, ..., х_m)^ вектор входных координат, Т знак транспонирования. Проведено n экспериментов, в каждом из которых, при известных значениях входных координат х_j, определялись соответствующие им в установившемся режиме значения y_j выходной координаты (j – номер эксперимента). Требуется построить математическую модель объекта.

Уточним, что в данном случае может служить моделью объекта. Поскольку на выходную координату объекта, помимо учитываемых входных координат, всегда влияют и не учитываемые переменные, которые рассматриваются как некоторые случайные величины помехи, то определяемые экспериментально значения выходной координаты тоже случайны. В связи с этим выходная координата у зависит от входных не функционально, а стохастически, вероятностно. В этом случае связь, существующая между переменными х и у, называется корреляционной связью.

Зависимость математического ожидания выходной координаты у от х называется регрессионной зависимостью. Она и может в данном случае служить математической моделью объекта. Кривая, описывающая зависимость от х, называется кривой регрессии. Пример кривой регрессии приведен на рисунке 1.2.

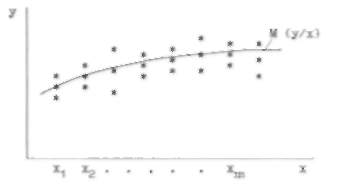
Рисунок 1.2 – Кривая регрессии

При построении модели в нашем распоряжении имеется совокупность экспериментально полученных значений входных и выходной координаты. Ни соответствует совокупность точек в пространстве , если объект имеет одну входную координату х (см. рисунок 1.3).

Рисунок 1.3 – Расположение кривой регрессии относительно экспериментальных точек

Ясно, что кривая регрессии должна проходить вблизи экспериментальных точек. Точнее, значения выходной переменной находимой но модели при условии, что входные координаты приняли значение (j – номер эксперимента), должны быть близки к значениям выходной координаты у_j, определенным экспериментально при тех же значениях входных переменных. Это условие и используется при построении модели. Для этого сформируем функцию F, оценивающую невязку ε – степень отклонения от , . Эти отклонения указаны на рисунке 3 применительно к случаю, когда объект имеет одну входную координату. В методе наименьших квадратов, используется квадрат невязки:

.

Вид зависимости задается. В общем виде зависимость можно представить в виде:

(1.1)

где (b₀, b₁, …, b_p) – вектор параметров модели (коэффициенты).

Задача состоит в том, чтобы по опытным данным наилучшим образом определить значения параметров .

В этом случае метод наименьших квадратов сводится к следующему. Наилучшими будут те значения параметров , при которых сумма квадратов отклонений расчетных величин от опытных окажется наименьшей.

Учитывая, что при нахождении параметров количество экспериментов n постоянно, степень близости модели и объекта будет оцениваться величиной:

(1.2)

Таким образом, в методе наименьших квадратов параметры находятся из условия:

,

т.е. являются решением задачи минимизации суммы квадратов невязки (этим и объясняйся название метода).

Покажем, как решается эта задача.

Пусть функция задана в общем виде (I). Структуру модели, входящие в нее входные координаты или функции от них, можно затем уточнить. Запишем условия всех опытов в виде таблицы матрицы плана эксперимента:

(1.3)

Здесь каждая строка – условие одного опыта; каждый столбец – значения одной переменной в разных опытах; х₁₃ – значения 1-й переменной в 3-м опыте. Рассмотрим также вектор-столбец результатов эксперимента:

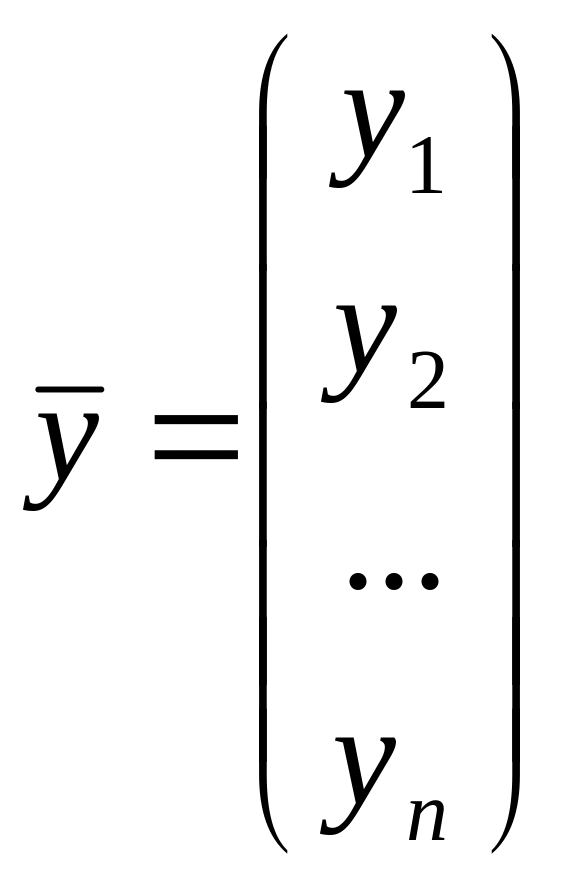(1.4)

Расчетное значение для j-той строки матрицы будет иметь вид:

(1.5)

Приведенное выше определение метода наименьших квадратов может быть записано формулой:

. (1.6)

Те значения , при которых сумма S окажется минимальной, и будут наилучшими.

Проше всего расчет методом наименьших квадратов, осуществляется, когда уравнение (I) линейно относительно коэффициентов . Это значит, что его можно записать в следующем виде:

(1.7)

Здесь x₀ фиктивная переменная, тождественно равная единице. Она вводится для симметрии для того, чтобы все параметры, и в том числе b₀, входили в модель единообразно. Это упрощает выкладки.

Рассмотрим расчет коэффициентов для этого случая. Матрица x будет иметь вид:

(1.8)

Квадрат разности для 3-го опыта запишется так:

(1.9)

Подставляя зависимость (9) в выражение (6), получим:

(1.10)

Необходимым условием минимума функции является равенство нулю ее частных производных по искомым параметрам (поскольку функция является квадратической, то эти условия выделяют единственную точку минимума).

, , …,

или

Запишем эту систему в виде, удобном для анализа,

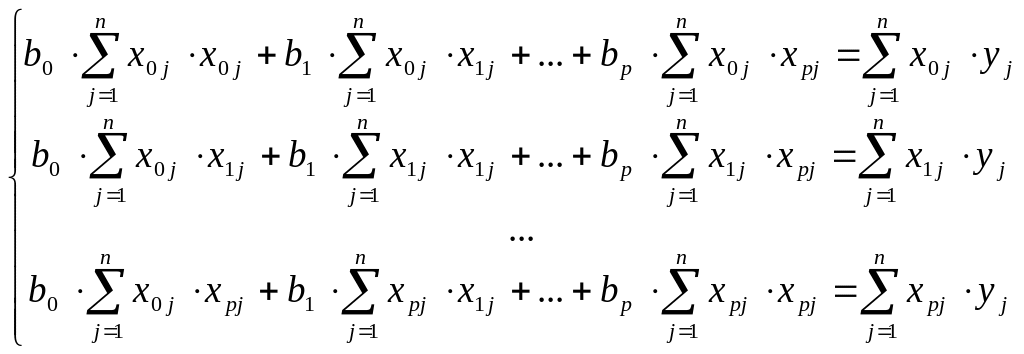(1.11)

Полученная система линейных алгебраических уравнений содержит столько уравнений, сколько в нее входит неизвестных параметров b. В теории метода систему (1.11) принято называть системой нормальных уравнений.

Система нормальных уравнений может быть решена, например, по правилу Крамера, согласно которому b₁ = Δ₁/Δ, где Δ – определитель матрицы системы нормальных уравнений:

а Δ₁ получается из Δ путем замены 1-го столбца на столбец

Решение может быть сравнительна точно найдено, если матрица системы нормальных уравнений не является плохо обусловленной, т.е. определитель Δ существенно отличается от нуля. В противном случае, при вычислении b₁, Δ₁ будет делиться на величину, близкую к нулю. В этом случае необходимо либо менять структуру модели, либо менять выборку экспериментальных данных.

Пример: Расчет коэффициентов методом наименьших квадратов.

По опытным данным построить зависимость плотности жидкости от температуры в виде параболы 2-й степени.

Т, К	273	283	293	303
ρ, кг/м3	875	871	868	867

Для уменьшения расчетов удобно преобразовать переменные так, чтобы они выражались малым числом цифр.

Так вместо Т можно использовать величину х = (Т – 288)/5, а вместо ρ у = ρ – 870.

Тогда зависимость получит вид:

.

Представим опытные данные х и у

х	-3	-1	1	3
у	5	1	-2	-3

В первом столбце матрицы плана во всех строках стоят значения х₀ = 1, во втором столбце значения х, в третьем значения х². Окончательно эта матрица имеет вид:

Система нормальных уравнений получится по формуле (1.11)

Определитель матрицы системы нормальных уравнений

.

; ; .

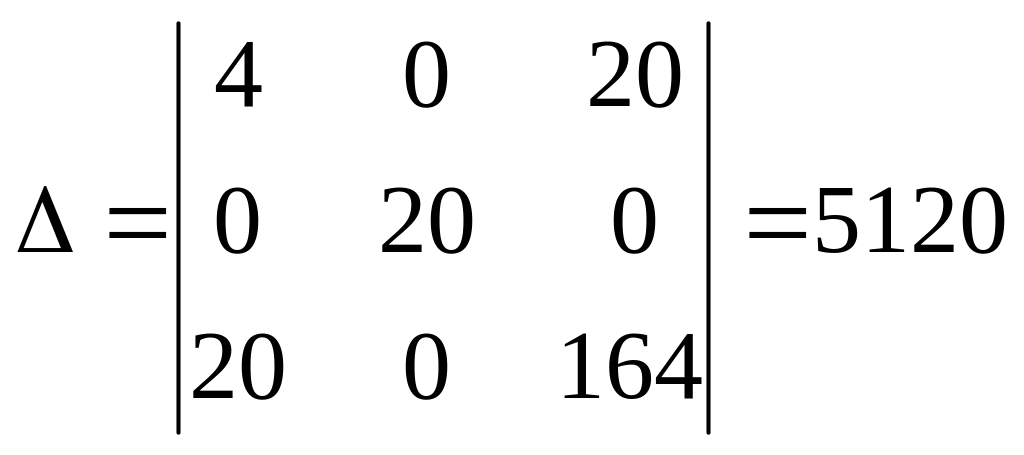Откуда

; ; ,

или

.

Окончательно

.

При большом числе искомых параметров построение регрессионного уравнения требует громоздких вычислений. В связи с этим в настоящее время построение регрессионных зависимостей практически всегда производится с применением ЭВМ. В этом случае удобно использовать матричный способ представления и обработки информации. Нетрудно убедиться, что матрица коэффициентов левых частей системы равна произведению матрицы на транспонированную матрицу :

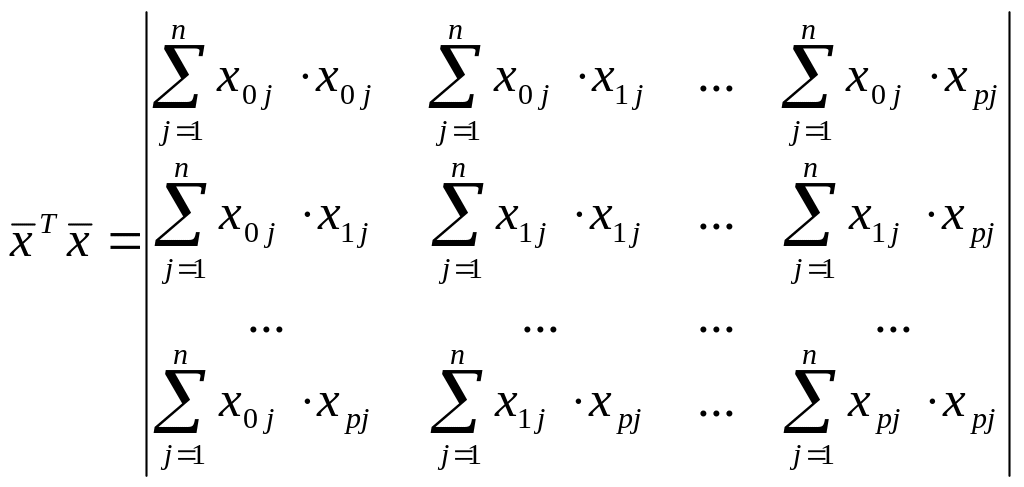(1.12)

Вектор-столбец правых частей системы нормальных уравнений равен произведению , где – вектор (4)

(1.13)

В матричных обозначениях решение системы (11) имеет вид

(1.14)

где индекс -1 есть символ обращения матрицы; – вектор исходных параметров. Это соотношение и используется для нахождения параметров модели.

Отметим, что если объект имеет несколько выходных координат, то для каждой выходной координаты ее зависимость от входных переменных находится отдельно.