1.4 Средние показатели

Наиболее распространенной формой статистических показателей, используемой в социально-экономических исследованиях, является средняя величина, представляющая собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени. Показатель в форме средней величины выражает типичные черты и дает обобщенную характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности. Широкое применение средних объясняется тем, что они имеют ряд положительных свойств, делающих их незаменимыми в анализе явлёний и процессов общественной жизни.

Важнейшее свойство среднего показателя заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности. Значение признака отдельных единиц совокупности могут колебаться в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные. Например, доходы такой социальной группы, как студенты государственных вузов, в целом определяются действующим положением о начислении стипендии. В то же время доходы отдельно взятого студента могут быть очень большими (предположим, вследствие хорошо оплачиваемых сезонных работ, либо работа в свободное время), и совсем отсутствовать (например, при нахождении в академическом отпуске). Сущность средней в том и заключается, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Возможно, что ни один студент в границах исследуемой совокупности не имеет с точностью до рубля такого дохода, какой получен на основе расчёта средней. Однако эта средняя отражает тот типичный уровень доходов, который характеризует студенчество как социальную группу.[1, с.161]

Категорию средней можно раскрыть через понятие ее определяющего свойства. Согласно этому понятию средняя, являясь обобщающей характеристикой всей совокупности, должна ориентироваться на определенную величину, связанную со всеми единицами этой совокупности. Эту величину можно представить в виде функции:

f (х₁, х₂, ..., х_n).[2, с.60]    

Так как данная величина, в большинстве случаев, отражает реальную экономическую категорию, понятие определяющего свойства средней иногда заменяют понятием определяющего показателя.

Если в приведенной выше функции все величины х₁, х₂, ..., х_n заменить их средней величиной , то значение этой функции должно остаться прежним:

 [1, с.163]   

Исходя из данного равенства и определяется средняя. На практике определить среднюю во многих случаях можно через исходное соотношение средней (ИСС) или ее логическую формулу:

[1, с.163]

Так, например, для расчета средней заработной платы работников предприятия необходимо общий фонд заработной платы разделить на число работников:

[2, с.146]

Числитель исходного соотношения средней представляет собой определяющий показатель. Для средней заработной платы таким определяющим показателем является фонд заработной платы. Независимо от того, какой первичной информацией мы располагаем - известен ли нам общий фонд заработной платы или заработная плата и численность работников, занятых на отдельных должностях, или какие-либо другие исходные данные - в любом случае среднюю заработную плату можно получить только через данное исходное соотношение средней.

Для каждого показателя, используемого в экономическом анализе, можно составить только одно истинное исходное соотношение для расчета средней. Если, например, требуется рассчитать средний размер вклада в банке, то исходное соотношение будет следующим:

[5, с.62]

Если же необходимо определить среднюю процентную ставку по кредитам, выданным на один и тот же срок, то потребуется следующее исходное соотношение:

[7, с.128]

Однако от того, в каком виде представлены исходные данные для расчета средней, зависит, каким именно образом будет реализовано ее исходное соотношение. В каждом конкретном случае для реализации исходного соотношения потребуется одна из следующих форм средней величины:

• средняя арифметическая;

• средняя гармоническая;

• средняя геометрическая;

• средняя квадратическая, кубическая и т.д.

Перечисленные средние объединяются в общей формуле средней степенной (при различной величине k):

     , где: х_i – i-ый вариант осредняемого признака ( ), f_i – вес i-го варианта. [1, с.164]

Помимо степенных средних в экономической практике также используются средние структурные, среди которых наиболее распространены мода и медиана. При осреднении уровней динамических рядов применяются различные виды средней хронологической.

Наиболее распространенным видом средних величин является средняя арифметическая, которая, как и все средние, в зависимости от характера имеющихся данных может быть простой или взвешенной. Эта форма средней используется в тех случаях, когда расчет осуществляется по несгруппированным данным.

Средняя арифметическая взвешенная. При расчете средних величин отдельные значения осредняемого признака могут повторяться, встречаться по несколько раз. В подобных случаях расчет средней производится по сгруппированным данным или вариационным рядам, которые могут быть дискретными или интервальными.

Свойства средней арифметической.

Средняя арифметическая обладает некоторыми математическими свойствами, более полно раскрывающими ее сущность и в ряде случаев используемыми при ее расчете. Рассмотрим эти свойства:

1. Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие им частоты:

    

Действительно, если мы обратимся к приведенному выше примеру расчета среднего курса продажи акций, то получим следующее равенство (за счет округления среднего курса правая и левая части равенства в данном случае будут несколько отличаться):

417,03 · 1850 = 420 · 700 + 440 · 200 + 410 · 950

2. Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю:

    

Для нашего примера:

(420 - 417,03) · 700 + (440 - 417,03) · 200 + (410 - 417,03) · 950 ≈ 0

Математическое доказательство данного свойства сводится к следующему:

3. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной величины С:

    

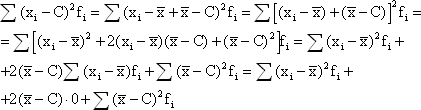
Следовательно, сумма квадратов отклонений индивидуальных значений признака от произвольной величины С больше суммы квадратов их отклонений от своей средней на величину

На использовании этого свойства базируется расчет центральных моментов, представляющих собой характеристики вариационного ряда при C = :

где k определяет порядок момента (центральный момент второго порядка представляет собой дисперсию).

4. Если все осредняемые варианты уменьшить или увеличить на постоянное число А, то средняя арифметическая соответственно уменьшится или увеличится на ту же величину:

    

Так, если все курсы продажи акций увеличить на 15 руб., то средний курс также увеличится на 15 руб.:

5. Если все варианты значений признака уменьшить или увеличить в А раз, то средняя также соответственно увеличится или уменьшится в А раз:

    

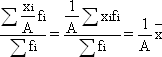
Предположим, курс продажи в каждом случае возрастет в 2 раза. Тогда и средний курс также увеличится на 100%:

6. Если все веса уменьшить или увеличить в А раз, то средняя арифметическая от этого не изменится:

    

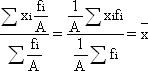
Так, в нашем примере удобнее было бы рассчитывать среднюю, предварительно поделив все веса на 100:

Исходя из данного свойства, можно заключить, что если все веса равны между собой, то расчеты по средней арифметической взвешенной и средней арифметической невзвешенной приведут к одному и тому же результату.[1, с.168]

Кроме средней арифметической при расчете статистических показателей могут использоваться и другие виды средних. Однако, в каждом конкретном случае, в зависимости от характера имеющихся данных, существует только одно истинное среднее значение показателя, являющееся следствием реализации его исходного соотношения.

Средняя гармоническая взвешенная используется, когда известен числитель исходного соотношения средней, но неизвестен его знаменатель. Рассмотрим расчет средней урожайности, являющейся одним из основных показателей эффективности производства в агробизнесе:

Средняя гармоническая невзвешенная. Эта форма средней, используемая значительно реже, имеет следующий вид:

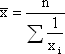    [1, с.172]

Средняя геометрическая. Еще одной формулой, по которой может осуществляться расчет среднего показателя, является средняя геометрическая:

- невзвешенная

- взвешенная

Наиболее широкое применение этот вид средней получил в анализе динамики для определения среднего темпа роста, что будет рассмотрено в соответствующей главе.

Средняя квадратическая. В основе вычислений ряда сводных расчетных показателей лежит средняя квадратическая:

- невзвешенная

- взвешенная [5,с. 70]

Наиболее широко этот вид средней используется при расчете показателей вариации.

В статистическом анализе также применяются степенные средние 3 го порядка и более высоких порядков.