Задача №9
Тема: РОЗРАХУНОК ДОТИЧНИХ НАПРУЖЕНЬ В БРУСІ
9.1 Основні відомості
(Див. розділ 8.1)
9.2 Постановка задачі
Скласти блок-схему алгоритму і програму алгоритмічною мовою, які б дозволили у табличному вигляді видавати на друк відношення дотичних напружень , що виникають в прямокутних перерізах бруса, до сили перерізу на різних висотах від центральної осі .
Знайти екстремальні значення відношень , а також точки , в яких вони досягаються. Результати обчислень вивести на друк.
Розрахункові формули для дотичних напружень в перерізі бруса і вхідні дані для програми задані в таблицях 8.1 та 8.2.
Задача №10
Тема: РОЗРАХУНОК КРИТИЧНОЇ ЧАСТОТИ ОБЕРТАННЯ ВАЛА
10.1 Основні відомості
Коли швидкість
вала, на якому знаходяться тіла обертання,
співпадає з кутовою швидкістю
,
яка характеризує власну частоту
поперечних коливань системи, виникає
резонанс. При цьому згин вала значно
збільшується, що може виявитися
небезпечним. Частоту обертання, що
відповідає резонансу, називають
критичною. Звичайно для вала існує
декілька критичних частот обертання,
із яких, як правило, вказуються лише
мінімальна [2,
3].
Якщо припустити, що
ваги
тіл обертання, встановлених на валу;
– статичні згини вала в місцях кріплення
тіл обертання;
–
прискорення вільного падіння, то можна
наближено власну кутову швидкість
(рад/с) записати таким чином:
. (10.1)
Знаючи кутову швидкість,
можна визначити статичну частоту
(об/хв)
. (10.2)
10.2 Постановка задачі
На рисунку 10.1 показаний вал постійного перерізу, який можна розглядати як брус з двома опорами.
Скласти блок-схему алгоритму і програму алгоритмічною мовою для обчислення критичної частоти обертання вала .
Розглянемо брус, на який
діють
зосереджених сил (рисунок 10.2). Силі
,
прикладеній в точці
,
відповідає згин
.
При визначенні згинів в розглянутому
випадку можна вважати, що справедливий
принцип суперпозицій і з урахуванням
цих припущень згин можна визначити за
формулою
, (10.3)
де – відстань між опорами;
– момент інерції перерізу;
– модуль пружності матеріалу;
– число встановлених на валу тіл обертання;
– ваги тіл обертання;
– координати точок кріплення тіл.
Вважаючи
з урахуванням приведеної вище залежності,
визначимо статичні згини, обумовлені
вагами обертових тіл, встановлених на
валу. За формулами (10.1), (10.2) обчислимо
критичну частину обертання
.
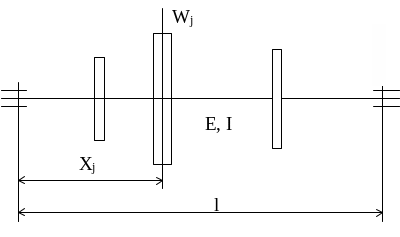
Рисунок 10.1 - Вал з встановленими на ньому тілами обертання
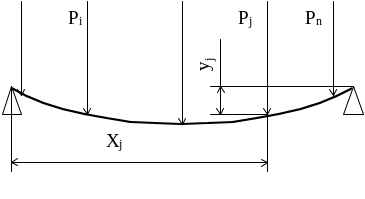
Рисунок 10.2 - Згин вала при дії зосереджених сил
10.3 Варіанти завдань
Таблиця 10.1 – Варіанти завдань
№№ варі-анта |
Модуль пружності , МПа |
Момент інерції перерізу вала , см4 |
Віддаль між опорами , см |
Число тіл обертання |
Ваги тіл обертання , кгс |
Координати розміщення тіла обертання , см |
1 |
210000 |
33 |
230 |
3 |
36; 54; 20 |
76; 120; 20 |
2 |
200000 |
32 |
240 |
4 |
34; 42; 36; 40 |
63; 90; 120; 200 |
3 |
120000 |
34 |
235 |
3 |
30; 60; 40 |
80; 125; 205 |
4 |
215000 |
35 |
250 |
5 |
30; 36; 50; 54; 20 |
70; 90; 120; 165; 200 |
5 |
200000 |
36 |
245 |
6 |
32; 38; 40; 50; 60; 20 |
75; 100; 110; 150; 190; 210 |